【例7.5】取余运算（mod）快速幂

本文主要是介绍【例7.5】取余运算（mod）快速幂，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1326：【例7.5】取余运算（mod）

时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
输入b，p，k的值，求bpmodk
的值。其中b，p，k×k为长整型数。

【输入】
输入b，p，k的值。

【输出】
求 bp mod k的值。

【输入样例】
2 10 9
【输出样例】
2^10 mod 9=7

思路：

可以直接暴力，for循环慢慢做，然后再Mod，~~但是看起来不是很聪明的样子所以需要一个新的方法~~
- 快速幂之所以快速，是因为计算a^b 时，不是暴力解决：每次都*a，而是通过a^2, a^4 , a^8 , a^16，，，，这样依次时求次数的2倍数的幂的方法，因此时间大大缩短
- 有的次数不全是2的n次方，因此考虑到将其次数n转化为2的n次方相乘就行（a^b1 * a^b2 * a*^b3 = a^(b1+b2+b3) ,保证b1,b2,b3都是2的次方就行，例如2^34 = 2^5 * 2^1 。这么看，其实质就是将b转化为二进制，然后将其位数为1 是需要相乘。
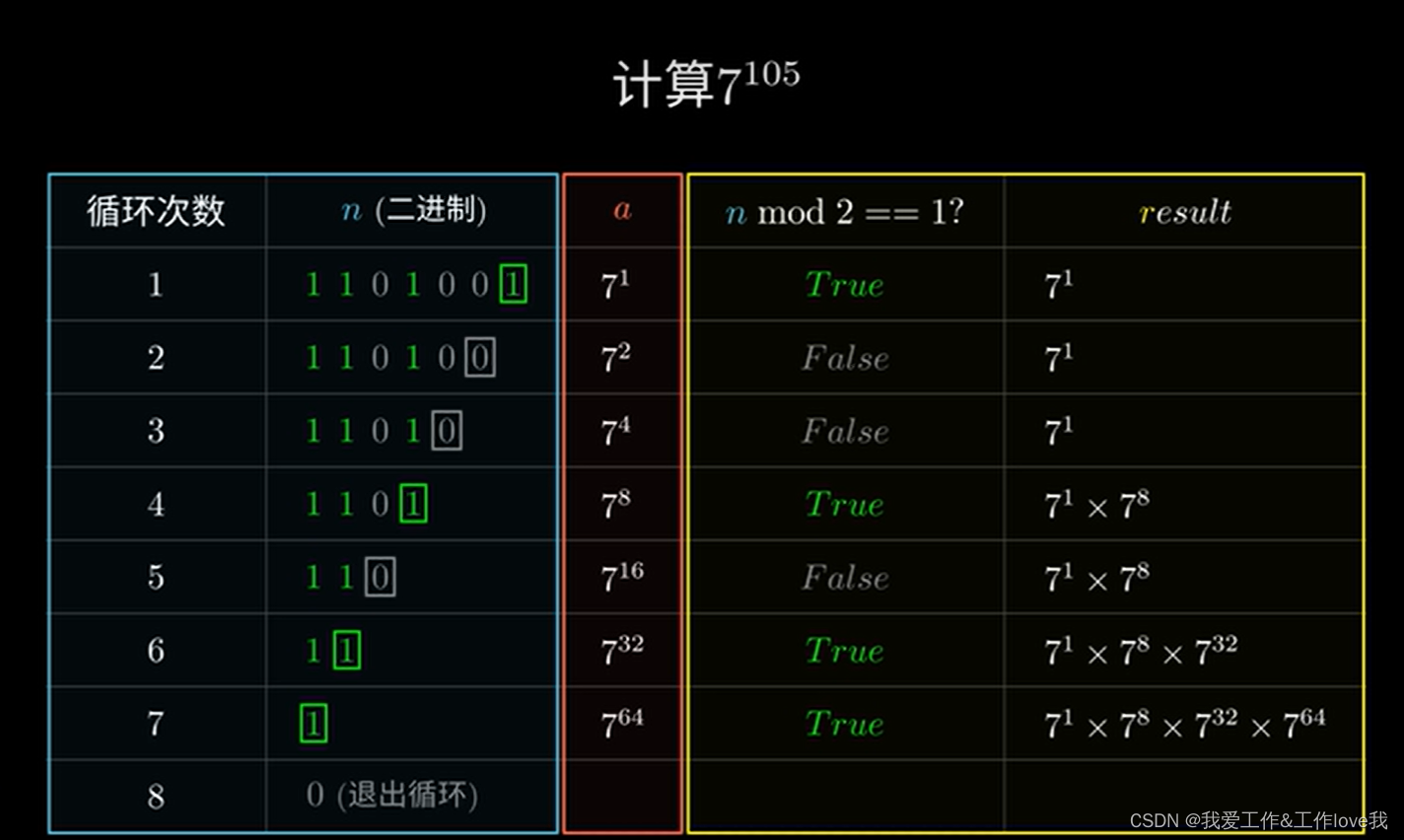
- 解决的a的次方就直接循环可以搞定，判断其位数是否为1实质就是b%2判断是否为1 即可
快速幂解决后，求mod，可以直接用结果求mod，也可以用数论公式(a*b)%p =(a%p* b%p)%p，每一步求Mod,再将最后结果求mod

示例代码：

#include<bits/stdc++.h>
using namespace std;
long long a,b,p;
long long answer=1;
int main()
{cin>>a>>b>>p;//定义底数，次数，取余 int k=a;long long tmp=b; // while(b!=0){if(b%2==1)   //相当于计算二进制数该位数是否为1 answer=(answer*a)%p;  //如果是1，则开始计算（再取模） a=(a*a)%p; //每次将该数直接求其平方（再取模） b=b/2;//由于求的是数的平方，所以次数需要/2 }answer=answer%p;//再将结果取mod a*b%p =(a%p*b%p)%P cout<<k<<"^"<<tmp<<" mod "<<p<<"="<<answer;return 0;
}