关联矩阵专题
有向无环图的关联矩阵及其矩阵乘积的含义
有向无环图的关联矩阵及其矩阵乘积的含义 引言关联矩阵的定义矩阵乘积 B B T BB^T BBT的含义伪代码示例C代码示例结论 引言 在计算机科学和数学中,有向无环图(Directed Acyclic Graph, DAG)是一种常见的数据结构,广泛应用于各种算法中,如拓扑排序、动态规划等。在有向无环图中,关联矩阵(incidence matrix)是一种表示图中顶点与边之间关系
邻接矩阵、可达性矩阵、完全关联矩阵、可达性矩阵的计算
邻接矩阵:很简单,就是两个点有关系就是1,没有关系就是0 可达性矩阵:非常简单,两点之间有路为1,没有路为0 可发行矩阵的计算:有n个元素,初始可达性矩阵为A,那么最终的矩阵B= 完全关联矩阵:描述点与边的关系,如果该点和该边有关系为1,没有关系就为0,非常简单 注意:对于无向图来说,只需要考虑边和点之间有没有关系,有关系即为1,没有关系即为0;但是对于有向图来说,点与
python提取特征、键值对关系到关联矩阵
首先是待处理数据 test = pd.read_csv('../test_pairs.csv')test.head(10) 输出: pairId FirstId SecondId0 0 1427 80531 1 17044 76812 2 19237 209663 3 8005 207654 4 16837 5995 5 3657 125046 6 2836 75
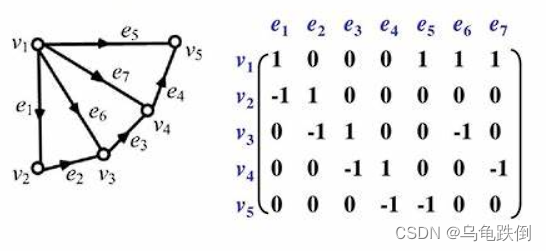
MIT线性代数笔记十二 图、网络、关联矩阵
本讲讨论线性代数在物理系统中的应用。可参考链接为:https://www.juanklopper.com/wp-content/uploads/2015/03/I_13_Graphs_Incidence_matrices_Kirchhoff_laws.html 文章目录 1. 图和网络 Graphs & Networks2. 关联矩阵(Incidence matrices)2.1 零空间