二阶可导点是拐点的必要条件 设  存在，且点 （x0，f(x0) ) 为曲线拐点，则    判断拐点的第一充分条件 设 f(x) 在 x=x0 处连续，在点 x=x0 的某去心邻域  内二阶导数存在，且在该点的左右邻域内  变号 则点 （x0，f(x0) ) 为曲线拐点   判断拐点的第二充分条件 设 f(x) 在 x=x0 的某邻域内三阶可导，且  ,则点 （x0，f(x0) )

一阶可导点是极值点的必要条件 设 f(x) 在 x=x0 处可导，且在点 x0 处取得极值，则必有    判断极值的第一充分条件 设 f(x) 在 x=x0 处连续，且在 x0 的某去心邻域  内可导  x0 极小值点x0 极大值点   判断极值的第二充分条件 设 f(x) 在 x=x0 处二阶可导，且  x0 极大值点 x0 极小值点   判断极值的第三充分条件 设

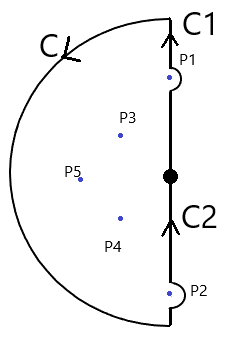
Routh-Hurwitz准则——判别实系数多项式有无实部非负的根的充要条件 一、引言二、准则内容三、举例说明四、证明思路五、证明引理1引理2①沿着C②沿着C1（C2同理，因为是对称的） 六、证明思路梗概七、参考文献/书籍 本文为 该知乎文章搬运到CSDN的文章， 该文章作者与本文章为同一人，内容是本人原创。之所以搬运到CSDN，是因为CSDN的markdown编辑器比较好用，