young专题

线性代数|机器学习-P8矩阵低秩近似eckart-young

文章目录 1. SVD奇异值分解2. Eckart-Young2.1 范数 3. Q A = Q U Σ V T QA=QU\Sigma V^T QA=QUΣVT4. 主成分分析图像表示 1. SVD奇异值分解我们知道，对于任意矩阵A来说，我们可以将其通过SVD奇异值分解得到 A = U Σ V T A=U\Sigma V^T A=UΣVT，通过 Σ \Sigma Σ中可以看

29、亲身体验Young GC风暴：模拟教程带你走进GC的神秘世界！

29.1、前文回顾在今天的文章，我们将通过代码演示来展示年轻代的Young GC是如何发生的。同时，我们还将指导大家如何在JVM参数中配置打印对应的GC日志。接下来，我们将通过分析GC日志，逐步解析JVM的垃圾回收机制是如何运作的。 29.2、不可不知的JVM参数设置技巧首先，根据我们之前的学习，我们知道，在系统运行过程中创建的对象，通常都是优先分配在新生代中的Eden区域。当然，这是针

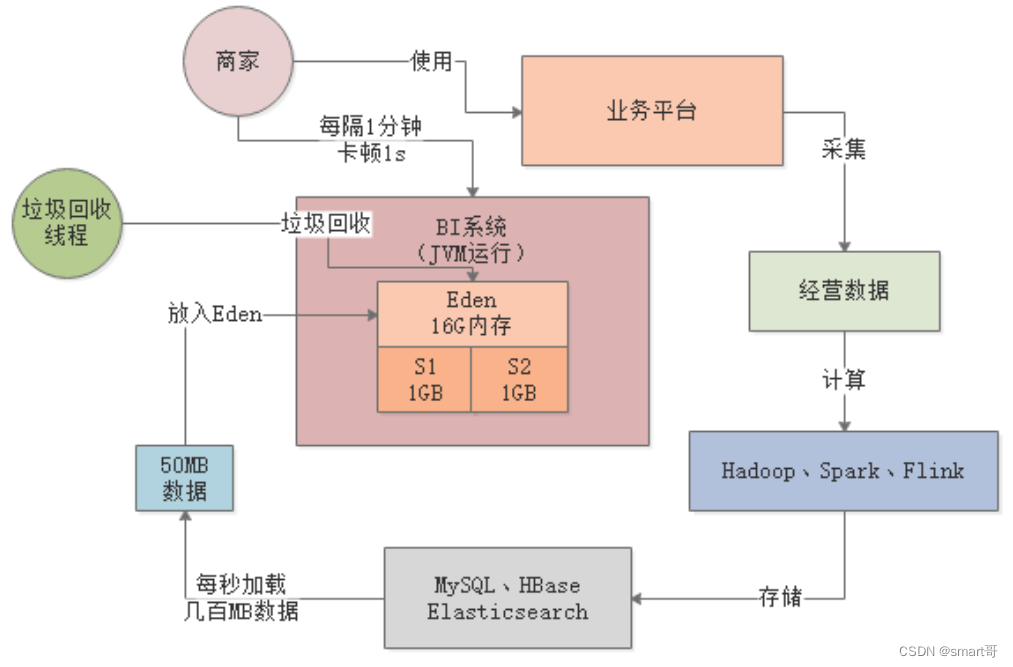
模拟每秒10万并发的BI系统,观察频繁Young GC

代码: vm option -XX:NewSize=104857600 -XX:MaxNewSize=104857600 -XX:InitialHeapSize=209715200 -XX:MaxHeapSize=209715200 -XX:SurvivorRatio=8 -XX:MaxTenuringThreshold=15 -XX:PretenureSizeThreshold=314572

JVM10_堆空间之新生代老年代、内存分配过程、Minor GC（Young GC）、Major GC、Full GC、TLAB、逃逸分析

要想设置新生代中的比例，必须显式指定SurvivorRatio, 只是关闭自适应分配策略不管用对象内存分配过程图解自我总结过程：首先new的对象会放在Eden区，当Eden区满了以后会触发YoungGC（Minor GC），此时会把没有被GC的对象放到S0或者S1区，假设此时就是放到了S0区。当对象被放到S区开始，就会为这些对象分配一个age年龄计数器（当到了一定年龄

安踏携手年轻人，如何跑出不一YOUNG？

营收逼近500亿元大关，同比增长38.9%。如果将安踏体育这份2021年成绩单与两家国际巨头中国全资公司的同期收入相比，安踏约等于阿迪达斯中国的1.44倍，超越耐克中国仅剩一步之遥。2022年，安踏或能完成在中国市场的“双超”格局。舆论也反映了类似的动向，“安踏正在被年轻人买爆，国产运动品牌在华跑赢国外品牌”！在国潮崛起的大势中，中国年轻人正成为主力军力量。数据显示，安踏消费人群中，超

Roy A. Young，MarketingProfs总裁推荐《营销2.0最佳实践：网络营销时代的ANGELS制胜法则》...

推荐序二 ——Roy A. Young，MarketingProfs总裁当我们进入新千年的第一个十年，营销正在发生革命性的变化，传统的战略和规则逐步退出舞台。很大程度上是因为互联网和其他电子化沟通方式解放了消费者，他们能够很方便地研究所有可能的选择，并与供应商、经销商、专家和其他消费者沟通；加剧的竞争导致用户迁移成本极低，任何与主题无关的沟通都可能导致用户注意力的转移，甚至流失。今天的营销已

Roy A. Young，MarketingProfs总裁推荐《营销2.0最佳实践：网络营销时代的ANGELS制胜法则》

推荐序二 ——Roy A. Young，MarketingProfs总裁当我们进入新千年的第一个十年，营销正在发生革命性的变化，传统的战略和规则逐步退出舞台。很大程度上是因为互联网和其他电子化沟通方式解放了消费者，他们能够很方便地研究所有可能的选择，并与供应商、经销商、专家和其他消费者沟通；加剧的竞争导致用户迁移成本极低，任何与主题无关的沟通都可能导致用户注意力的转移，甚至流失。今天的营销已

#动态规划 or 杨氏矩阵，勾长公式#poj 2279 Mr. Young's Picture Permutations

题目有n行，人数依次递减，而行内的顺序也是递减，问一共有多少种方案（动态规划）分析可以用一个5维dp，具体就是一次又一次增加，注意动态开内存代码 #include <cstdio>#include <cstring>int n,a[5];int in(){int ans=0; char c=getchar();while (c<48||c>57) c=getchar

JVM实战（14）——Young GC调优

作者简介：大家好，我是smart哥，前中兴通讯、美团架构师，现某互联网公司CTO 联系qq：184480602，加我进群，大家一起学习，一起进步，一起对抗互联网寒冬学习必须往深处挖，挖的越深，基础越扎实！阶段1、深入多线程阶段2、深入多线程设计模式阶段3、深入juc源码解析阶段4、深入jdk其余源码解析阶段5、深入jvm源码解析一、简介本章，我们还是以案例驱动的方式讲解You

ARM Linux 如何模拟X86 PTE中的Present Young和Dirty标志位

ARM Linux 如何模拟X86 PTE中的Present Young和Dirty标志位原创文章，转载请注明出处.转载自: Li Haifeng's Blog 本文链接地址: ARM Linux 如何模拟X86 PTE中的Present Young和Dirty标志位注：本文是参考Kernel的代码并加上个人揣测，欢迎指正在 X86 MMU Page table

Young Tableau问题的随笔

Young Tableau问题的描述是这样的,一个由N个小方块组成的阵列(不一定要是矩形,可以是一个任意"光滑"且"单调"的组合),从1到N这N个数填入方块中,要求全部填满并且一个数只能填一个方格一次.并且满足,每个数的上方的数和左方的数比它大.求最后一共有多少种填法.比如一个4*4格子的正方形,1~16这16个数按照上述规则填入,那么一共多少种填法. 笔者根据理解,还是用程序实现了一下算了

Letter to a Young Developer

I’ve been getting some emails from young developers wanting to “level up” as programmers. I’m definitely not the first to write about this topic, so I’m not sure how much I have to add. Still, for

CF1268B Domino for Young （黑白染色）

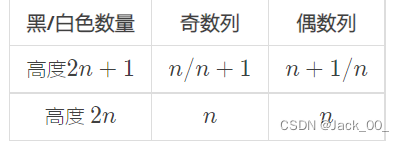
Problem - 1268B - Codeforces 给出一个不规则的网格。共 nn 列,每列有 a_iai 个格子。现在要将 1 \times 21×2 的骨牌不重叠的覆盖在网格上，求最多能放的骨牌数量。网格满足条件高度左到右递减。题解：比较经典的骨牌填棋盘问题。有神仙结论就是假如黑白间隔染色后，那么染出来的东西就一定可以用1*2的骨牌填满。那么考虑填上即可。假

打印JSON对象时，如果内部键值为null，则该键不会打印出来，too young too naive

几年前博主在GitHub提的一个问题，记录下! 打印JSON对象时，如果内部键值为null，则该键不会打印出来 JSONObject{“a”:1,“b”:"",“c”:null,“d”:“loongshawn”} 打印出来JSONObject{“a”:1,“b”:"",“d”:“loongshawn”}，作如何解释… 问题来源：https://github.com/alibaba/fas