trailing专题
UVA - 11029Leading and Trailing(快速幂取模取后三位 + log10()取前三位)
题目: UVA - 11029Leading and Trailing(快速幂取模取后三位 + log10()取前三位) 题目大意:给你N的k次方,然后要求你求出这个数的前三位和后三位。 解题思路:因为n和k都很大,这个数求出来是大数,所以可以用快速幂取模求后三位,因为后面的三位和前面的位数的没有关系。前面的三位比较难办。设x = log (n^k) = k * log10(n)
Light OJ 1028 Trailing Zeroes (I) 求n因子数
题目来源:Light OJ 1028 题意:求一个数转化成任意进制后末尾有0的种数 就是一个数因子的个数 思路:一个数可以被分解成若干素数相乘 p1^x1*p2^x2*...*pn^xn 根据乘法原理 因子数为 (x1+1)*(x2+1)*...*(xn+1) 注意剪枝 #include <cstdio>#include <cstring>#include <cmath>#inc
*lightoj 1138 Trailing Zeroes (III) | 二分+数学
这题问了杰神才知道怎么做。 题意: 给你Q,表示N!的结果后面有Q个零,让你求出最小的N为多少。若无法找到则输出impossible 思路: 根据唯一分解定理,一个自然数可以写成质数的幂次方的乘积。例如10 = 2^1 * 5^1 因为是尾部有Q个零,所以N!的结果中5的幂必须等于Q(此时,2的幂肯定比Q大)。 那么我们如果要求一个数的阶乘的结果5的幂次方是多少。 譬如30!的结果中
uva 11029 - Leading and Trailing(快速幂)
题目链接:uva 11029 - Leading and Trailing 题目大意:给出一个n和k求n^k的前三位数和后三位数。 解题思路:后三为数可以用分治的方法(快速幂)去做,可是前三位数就比较麻烦了,看了别人的题解. n^k = 10 ^ (k * log10(n)),所以可以将多余的位数移到小数点后面然后舍弃掉,只保留前三位,pow(10, 2 + fmod(k * l
[LeetCode] 172. Factorial Trailing Zeroes
题目内容 给定一个整数 n,返回 n! 结果尾数中零的数量。 示例 1:输入: 3输出: 0解释: 3! = 6, 尾数中没有零。示例 2:输入: 5输出: 1解释: 5! = 120, 尾数中有 1 个零. 题目思路 需要思考一下,到底什么情况下会出现0。那么根据经验,只要碰到包含因子5的数字,就会出现0.(包含5然后包含偶数,而且偶数的数量大于5的个数)。比如5!包含1个
《leetCode》:Factorial Trailing Zeroes
题目 Given an integer n, return the number of trailing zeroes in n!.Note: Your solution should be in logarithmic time complexity. 思路一:不能AC 思路,统计2和5的个数 ,时间复杂度为O(n) int min(int a,int b){return a<b?a:
LightOJ 1282 Leading and Trailing
题意:求n^k的前三位和后三位。(n,k为大数) 分析: 后三位可以用快速幂得到(不足三位要补领0)。重点是求前三位。 n可以写成10^a(a为小数)的形式。因此 n^k = 10^(ak). 而ak可以写成x+y,其中x为ak的整数部分,y为ak的小数部分.其中x决定了位数,y决定了值。 因此只需求出y。 而n=10^a ,所以 a=log10(n) 这里用到了fmod函数,fmod(
LeetCode(31)-Factorial Trailing Zeroes
题目: Given an integer n, return the number of trailing zeroes in n!.Note: Your solution should be in logarithmic time complexity. 思路: 题意是要求一个数字的阶乘,末尾有多少个0要求是对数级别的时间,所以考虑用递归分析一下,产生一个10,后面加0,找到所有的2*5,
LeetCode--172. Factorial Trailing Zeroes
Problem: Given an integer n, return the number of trailing zeroes in n!. Note: Your solution should be in logarithmic time complexity. Analysis: 对n!做质因数分解n!=2x*3y*5z*… 显然0的个数等于min(x,z),并且min(x,z
LeetCode题解——Factorial Trailing Zeroes
Given an integer n, return the number of trailing zeroes in n!. Note: Your solution should be in logarithmic time complexity. 出现0的情况是,出现5和2的倍数。 [n/k]代表1~n中能被k整除的个数,而能被2整除的个数多余能被5整除的个数,故只要知
Project Euler_Problem 160_Factorial Trailing Digits_费马小定理,威尔逊定理,左右互搏
原题目: 题目大意:1e12的阶乘,不算末尾的0,后5位数字为多少 解题思路: 暴力运算也能算,就是有点慢,优化过后可能也得算个几十分钟 这里考虑使用威尔逊定理+费马小定理 用这个方法我们就可以得到对于任何一个小于p的数n,p为素数,n!在模p下的结果, 对于本题: 则我们要找的答案应该是512628437919+k*39的最后几位有效数字,当k>100000时,显然末尾数字就
N - Trailing Zeroes (III)
题目链接:https://cn.vjudge.net/contest/70017#problem/N 题目大意:给你一个数n,让你求出后缀有n个零的最小的x!。 题解:二分1到5*1e8+5之间的数,然后计算这个数一直除以5的和。 代码; #include <iostream>#include <algorithm>#include <stdio.h>#include <stdlib
时序分析基本概念介绍Leading, Trailing edge
今天我们要介绍的时序分析概念是Leading, Trailing edge。 中文含义为主导,拖尾的边沿。 leading edge:主导的边沿,在每个周期中,第一个出现的边沿就是leading edge trailing edge:拖尾的边沿,在每个周期中,最后一个出现的边沿就是trailing edge leading edge不一定代表上升沿。反之,trailing edge也不一定
LeetCode Factorial Trailing Zeroes数学方法详解
Given an integer n, return the number of trailing zeroes in n!. 题目的意思是要求一个整数的阶乘末尾有多少个0; 1.需要注意的是后缀0是由2,5相乘得来,因此只需看有多少个2,5即可 n = 5: 5!的质因子中 (2 * 2 * 2 * 3 * 5)包含一个5和三个2。因而后缀0的个数是1。 n = 11: 11!的质因子中
python str ord chr 字符串赋值 trailing comma 尾巴逗号
Here are examples: a = '12y'# ch = ord(a) TypeError: ord() expected a character, but string of length 3 foundch = chr(ord(a[0])+1)print(ch) #2ch = chr(ord(a[2])+1)print(ch) #z#给字符串赋值没有太好的方式,切片是有效
Trailing Loves (or L'oeufs?) CodeForces - 1114C
http://codeforces.com/problemset/problem/1114/C 将b素因子拆分 形如b=(a1^p1)*(a2^p2)*...*(ak^pk) 凑出一个尾0 就需要p1个a1 p2个a2...pk个ak 然后看n能提供多少 取最小即可 #include <bits/stdc++.h>using namespace std;typedef long l
[LeetCode]172.Factorial Trailing Zeroes
题目 Given an integer n, return the number of trailing zeroes in n!. Note: Your solution should be in logarithmic time complexity. 分析 朴素解法: 首先求出n!,然后计算末尾0的个数。(重复÷10,直到余数非0) 该解法在输入的数字稍大时就会导致阶乘得数溢出,
[Leetcode]172. Factorial Trailing Zeroes
Given an integer n, return the number of trailing zeroes in n!. Note: Your solution should be in logarithmic time complexity. 我们对n!分解质因子,n!=2^x+3^y+5^z+...,结尾的0一定是1个2和1个5相乘得到的。很显然,这里因子5的个数小于因子2的个
hdu6069 Counting Divisors lightoj1028 - Trailing Zeroes (I)
由易到难:lightoj1028->hdu6069 lightoj1028 : http://www.lightoj.com/volume_showproblem.php?problem=1028 求一个数n,有多少种进制表示方法,使得末尾为0. 我们首先要想到这个n转化为其他进制如果末尾是0的话,只需要n可以整除这个数,换言之就是求n这个数在2-n范围内的约数。如果n很小的话(n<
Leetcode#172. Factorial Trailing Zeroes
题目描述:给定一个整数 n,计算 n! 末尾有多少个0 解题思路:虽然代码只有短短几行,但问题的解决是需要技巧的。 首先明确一个问题,n! 末尾若有0出现,那么一定是 2 * 5得来的,所以如果我们知道了 n! 中有多少个 2 * 5,那么就知道了末尾有多少个0;接下来,我们就想一想n! 中有多少个 2 * 5?有一个事实,在 n! 中,2的个数一定是大于5的个数的,有博主给出了证明,如下:
Light oj 1028 - Trailing Zeroes (I)
题目:Light oj 1028 - Trailing Zeroes (I) 思路:求约数个数减1 好久没做数学题了,于是TLE和WA了好几遍 = = 其实这个题3月份做的时候就TLE了。。。。。 参考的 article : Prime Factorization 发现自己以前写的质因数分解确实写的效率不高,那篇article里面的两个idea写的很清楚,= =第一个
uva11029 - Leading and Trailing(头和尾)
求前缀和后缀(分别三位) 后缀容易求,只是取模求幂。。。。每次乘方后都取最后三位, 至于前缀,以前做过类似的题目,,,对于n^k来说,肯定可以用科学计数法来表示,由于太大我们无法存储,而我们也不需要知道它有多大,我们只是要3位, 所以,,,只需要求出小数部分,,指数部分用log求出来,去除整数部分,求10的pow(),,得到的即科学计数法的小数部分, 表达式:P = k*log10(n)
leetcode 172. Factorial Trailing Zeroes求后面0的个数
Given an integer n, return the number of trailing zeroes in n!. Example 1: Input: 3Output: 0Explanation: 3! = 6, no trailing zero. Example 2: Input: 5Output: 1Explanation: 5! = 120, one traili
laravel Trailing data 问题解决
laravel Trailing data 问题解决 出现此问题一般是由于相关数据模型中created_at 的时间格式不正确导致的 比如 protected $table = 'ptn_apply_list';public $timestamps = true;protected $dateFormat = 'U';protected $guarded = []; 把其中
error Unexpected trailing comma comma-dangle
Error Unexpected trailing comma. comma-dangle 错误Eslint代码检测report数据。 原因是数据后多个逗号。
vue项目中报error Unexpected trailing comma comma-dangle
主要是eslint规则报错,是有一些文件还没有完成初始化,和你的eslint配置比匹配造成的,只需找到对应的文件,ctrl+s 就会好,前提是你配置了eslint规则



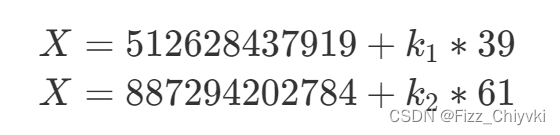

![[LeetCode]172.Factorial Trailing Zeroes](https://img-blog.csdn.net/20150207203556051)