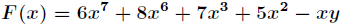strange专题
Light OJ 1318 Strange Game 组合数+快速幂+分解因子
长度为l的用k种字符组成的字符串有k^l中 其中m个字符要不相同 那就是k^l*C(l, m)*(k-1)^m 有重复 要除以2 但是你mod n了 不能直接除 n不一定是素数 所以不能乘以逆元 所以我都mod 2倍的n 最后的结果再除以2 特判l = 1 和 m = 0的情况 #include <cstdio>#include <cstring>#include <cmath>us
HDU 2899 Strange fuction(二分||三分)
题目链接~~> 做题感悟:这题和 2199 那题差不多。 解题思路:一、题目让求函数的最小值,首先应该分析函数图象。将函数求导得 f(x) ’ = 42 * x^6 + 48 * x^5 + 21 * x^2 + 10*x - y,因为 y 大于 0 所以假设存在 k 使f(x)'= 0,所以当0<=x<k 时f(x)’小于0,原函数在0<=x<k单调递减。在 k<x<=100 单调递增。
HDU2899 Strange fuction(牛顿迭代法)
最近刚学完数值分析上的方程求根——牛顿法,所以做几题练习一下。 Problem Description Now, here is a fuction: F(x) = 6 * x^7+8*x^6+7*x^3+5*x^2-y*x (0 <= x <=100) Can you find the minimum value when x is between 0 and 100.
很妙的思维题,CF 1270D. Strange Device
目录 一、题目 1、题目描述 2、输入/交互 2.1输入 2.2交互 3、原题链接 二、解题报告 1、思路分析 2、复杂度 3、代码详解 一、题目 1、题目描述 2、输入/交互 2.1输入 2.2交互 3、原题链接 Problem - 1270D - Codeforces 二、解题报告 1、思路分析 我们只考
HDU 2899 Strange fuction 水三分
<strong><span style="font-family:Comic Sans MS;font-size:24px;">题意不说了,思想就是三分很朴素</span></strong> #include<iostream>#include<stdio.h>#include<string.h>#define eps 1e-9using namespace std;double a;
Codeforces Contest 1191 F Tokitsukaze and Strange Rectangle —— sorting+线段树
This way 题意: 二维平面上有一些点,你现在有一个没有顶边的矩形,问你有多少种包含点的情况(每个点视为不同) 题解: 将每个点视为矩形下底边上的点,查找这个点左边有多少点,右边有多少点,这个点做完之后将其删除,相同高度的点从左到右做,对于右边的点要注意左端点位左边的点+1: 这张图就表示了相同高度右边点的可查询区间。 (刚多校结束发现2200真的是比赛中的简单题了) #incl
Codeforces Round#769(Div.2) C. Strange Test
题意 给定两个数,A-B,一共有三种操作 1.A=A+1; 2.B=B+1; 3.A=A|B; 问使得A=B的最小操作步数。 题解: 由于第一种操作和第二种操作不可能同时使用,所以要么是A++=B,要么是A++然后或为B,不然就是,用第三种操作使得A>=B,然后B++使得A=B(此时B为B变化后的值) #include<bits/stdc++.h>using namespace std;
uva 10519 !! Really Strange !!
原题: Raju has recently passed BSc. Engineering in Computer Science & Engineering from BUET (Bangladesh University of Extraordinary Talents), the best university of Bangladesh. After passing, he has be
G - Vitya and Strange Lesson(数组-字典树)
G - Vitya and Strange Lesson CodeForces - 842D Today at the lesson Vitya learned a very interesting function — mex. Mex of a sequence of numbers is the minimum non-negative number that is not pres
hdu 2988 Strange fuction【模拟退火】
计算:给出y , 的最小值 wa到哭啊,简直上火了,是板子没有套对, nex=now+T*i;//新解 T*i是变化的范围加上原先的才是新解, 还有精确度,因为评估函数要平方,所以要高一些 最终15ms #include<bits/stdc++.h>#define mp make_pair#define sz(x) int((x).size())#d
A strange lift
题目: There is a strange lift.The lift can stop can at every floor as you want, and there is a number Ki(0 <= Ki <= N) on every floor.The lift have just two buttons: up and down.When you at floor i,if
【动态规划】POJ_1958 Strange Towers of Hanoi
题意 输出n个盘子在4个塔的汉诺塔问题最少要多少步。 思路 我们设f[n]为n个盘子在4塔的汉诺塔问题下需要的最少步数,d[i]为i个盘子在3塔的汉诺塔问题下需要的最少步数,可以得出动态转移方程: f[n]=min(2∗f[i]+d[n−i]) f [ n ] = m i n ( 2 ∗ f [ i ] + d [ n − i ] ) f[n]=min(2*f[i]+d[n-i])
Life is Strange 奇异人生汉化指南
奇异人生汉化指南 引言:在搜索引擎上看了许多的攻略,都无法得到指向性明确的安装步骤,其中最令人不解的分别为汉化包与汉化包的安装地址,以下会以汉化包获取与汉化包安装地址两个维度来确保汉化的正确,以及在最终附上汉化成功截图。 文章目录 奇异人生汉化指南汉化包获取汉化包安装汉化成功 汉化包获取 汉化包的获取,在此感谢贴吧用户:查理有只猫; 汉化包百度云盘链接:提取码: m576
容斥 C. Strange Function改编题
补题: 题目详情 - 9.段坤爱取模%%% - SUSTOJ 本题或许是参考 Problem - C - Codeforces 根据题意,f(i)就是不能被整除的最小的一个质因子。 打表发现,当15个质因子相乘后,长度就大于18。 因此可以知道小于等于1e16内的正整数x,f(x)一定是前20个质因子之一,且合数一定不行。 前20个质因子:2 3 5 7 11 13 17 19 2
uvalive6468,51cthink1419 Strange Antennas (离散化)
题意: 在一个 n x n 的平面上,给定 m 个等腰直角三角形(各点均为整数),问该平面上被三角形覆盖奇数次的点有多少个。 思路: 由于 n 较大,不能模拟解决,故使用离散化思想。 考虑每一行有多少点被覆盖了奇数次,题目从二维转换成一维。 对于每一行,考虑每个三角形在此行覆盖的线段,记录下每条线段的左端点 l 、右端点 r 保存在同一个数组中。 排序后则容易知道第一个到第二个数、第三到第四个
ZOJ 2674 Strange Limit
ZOJ2674 Strange Limit source code (ZOJ2674.c) [recursion, number theory, Euler's theorem] 求a a..a%m!的极限。 欧拉定理的内容是:如果a和n互质,那么aφ(n)=1(mod n);对于任意a, n和较大的b>= φ(n) ,有ab=aφ(n)+b mod φ(n)(mod n)。