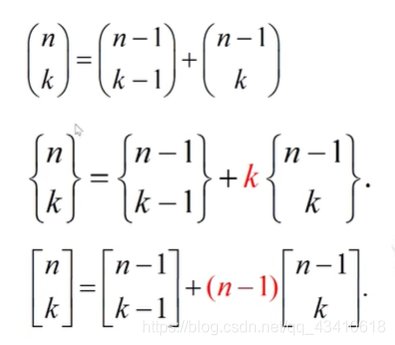stirling专题
组合数学 —— 斯特林数(Stirling)
【第一类斯特林数】 1.定理 第一类斯特林数 S1(n,m) 表示的是将 n 个不同元素构成 m 个圆排列的数目。 2.递推式 设人被标上1,2,.....p,则将这 p 个人排成 m 个圆有两种情况: 在一个圆圈里只有标号为 p 的人自己,排法有 S1(n-1,m-1) 个。p 至少和另一个人在一个圆圈里。 这些排法通过把 1,2....n-1 排成 m 个圆再把 n 放在 1,2.
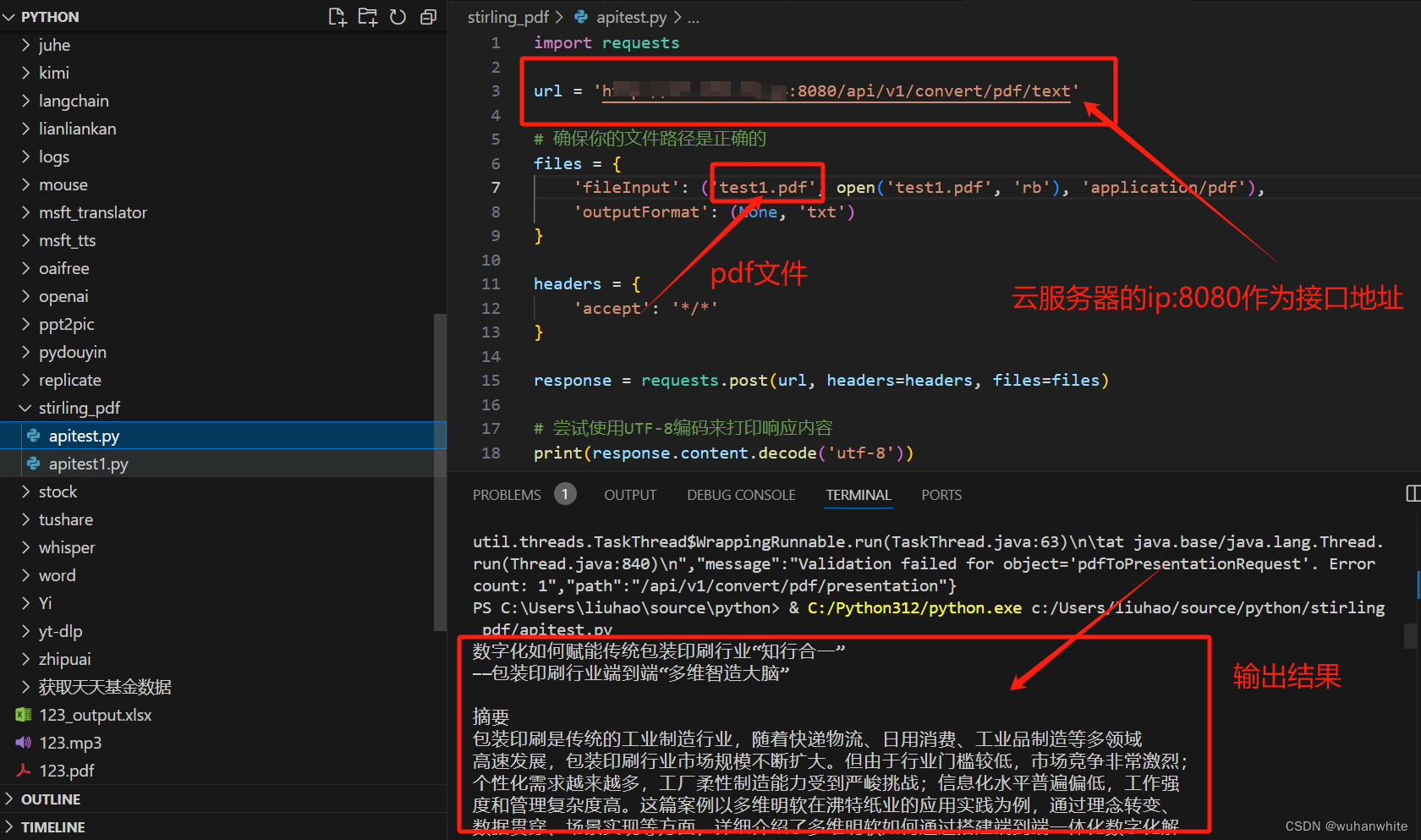
云端部署Stirling PDF:构建个人App的API调用指南(附Python源码)
今天发现一个Github的开源项目,Stirling PDF,项目地址如下:https://gitcode.com/Stirling-Tools/Stirling-PDFhttps://gitcode.com/Stirling-Tools/Stirling-PDF?utm_source=artical_gitcode目前CSDN上已经有好几个up主都介绍了这个项目,但是没有介绍如何用API的方式去
Vision_MATH_球盒问题+第二类Stirling数
///定义: /* 排列组合解决球盒的八大问题,其中用到排列组合公式和第二类斯特林公式 */ ///代码: /***name:第二类斯特林数(第二类Stirling数)**function:解决求不同盒同等问题**公式: S(r, c) = S(r-1,c-1) + c * S(r-1, c)*/#include <iostream>#inclu
使用docker安装本地pdf工具集合Stirling-PDF
平时工作中需要处理pdf,市面上的很多工具都需要充会员才能使用,偶然发现了一个可私有化部署且易于使用的PDF在线工具,使用docker部署,使用起来非常方便,而且功能齐全。 这里是官网: https://pdf.errui.cc/ 如果想本地部署 拉取镜像 docker pull frooodle/s-pdf:latest 运行Stirling-PDF容器 docker run
POJ 1430 Binary Stirling Numbers (斯特林数)
题意:给你n,k,求S(n,k) mod 2。 题解:没什么好说的,知道公式就好解决。C(z,w) = z! / [(w!) * (z-w)!],要判断奇偶性只需要统计一下分子分母的所含的因子2的个数。 #include<cstdio>#define lint __int64lint getTwo ( lint x ){lint cnt = 0, bit = 2;wh
Stirling PDF:免费PDF开源编辑工具
Git地址:https://github.com/Stirling-Tools/Stirling-PDF Stirling-PDF是一个基于spring-boot开发的开源项目,旨在提供一个功能强大的基于Docker的本地托管PDF操作工具。它使您能够对PDF文件进行多种操作,包括拆分、合并、转换、重新组织、添加图片、旋转、压缩等。该本地托管应用最初由ChatGPT完全开发,
斯特灵数stirling
Count the Buildings 不管是从左边看还是从右边看,视线总是会被中间最高的给挡住 所以我们把左边和右边分组来看。 对于某一边,我们确定出能够看见的楼房,那么不能够看见的楼房就可以任意排列 我们把能看见的楼房,与下一个能看到的楼房(不包括下一个楼房)之间的楼看为一组 可以考虑现将最高的拿出来,那么可以考虑左边需要有F-1个房子成递增关系,那么可以将左边的房子分成F-1个组(环),
使用Docker部署PDF多功能工具Stirling-PDF
1.服务器上安装docker 安装比较简单,这种安装的Docker不是最新版本,不过对于学习够用了,依次执行下面命令进行安装。 sudo apt install docker.iosudo systemctl start dockersudo systemctl enable docker 查看是否安装成功 $ docker -vDocker version 17.12.1-ce,
开源项目推荐:Frooodle/Stirling-PDF
简介一个本地的处理 PDF 的工具,界面是 Web UI,可以支持 Docker 部署。各种主要的 PDF 操作都可以支持。比如拆分、合并、转换格式、重新排列、添加图片、旋转、压缩等等。这个本地托管的网络应用最初完全由 ChatGPT 制作,后来逐渐发展,增加了许多功能,以满足你对 PDF 的各种需求。Stirling PDF 不会对外发送任何数据以进行记录或跟踪。所有的文件和 PDF 要么只在客
组合数学之Stirling数
Stirling估计式 n ! ∼ 2 π n ( n e ) n n! \sim \sqrt{2 \pi n}(\frac{n}{e})^n n!∼2πn (en)n 作用是为了方便计算n阶乘的复杂度 Stirling Numbers 第一类Stirling数 数学模型:n个人跳集体舞,分成m个圆环的方法数目 比如ABCD四个人跳舞,组成2个圆排列的方法有多少种? 可以是{AB
自然数幂和——第一类Stirling数和第二类Stirling数
第一类Stirling数 首先设 $$S_k(n)=\sum_{i=0}^ni^k$$ 根据第一类斯特林数的定义(P是排列数,C是组合数,s是Stirling) $$C_n^k={P_n^k\over k!}={\sum_{i=0}^k(-1)^{i+k}s(k,i)n^i\over k!}$$ 变形得 $$ n^k ={\sum_{i=0}^{k-1}(-1)^{i+k}s(k,i)n^i}-
知识点 - Stirling数
知识点 - Stirling数 解决问题类型: 将p个物体排成k个圆排列(非空循环排列)的方法数。从左往右会依次遇到A个比当前遇到的最大值更大的元素的排列的个数。(等价于上面的问题)表示将n个不同的元素拆分成k个集合的方案数。求泰勒展开系数每条边的长度为1,对每个节点u,求 E u = ∑ v = 1 n ( d ( u , v ) ) k , E_u = \sum_{v=1}^n (d(u,
The second kind of Stirling number(连载)
又要开新坑了,这可是个庞大工程。不定期更新!!! Definition: Stirling number of the second kind is the number of ways to partition a set of n objects into k non-empty subsets and is denoted by S(n,k) S(n,k) S(n,k)=S(n−1,
Stirling-PDF:一款优秀的开源PDF处理工具
最近我的朋友大雄需要将一个PDF转换为Word文档。于是他在网上尝试了多个PDF转换的在线工具,但要么需要会员,要么需要登录等繁琐操作,而且我们的文件也存在泄漏等安全隐患。因此,他向我咨询是否有可私有化部署且易于使用的PDF在线工具。大雄平时也喜欢制作PPT,每当有灵感时就会创建超过60多页的ppt演示文稿。 最近我在GitHub上闲逛时,恰好发现了一个名为Stirling-PDF的项目,该项目
Stirling-PDF:一款优秀的开源PDF处理工具
最近我的朋友大雄需要将一个PDF转换为Word文档。于是他在网上尝试了多个PDF转换的在线工具,但要么需要会员,要么需要登录等繁琐操作,而且我们的文件也存在泄漏等安全隐患。因此,他向我咨询是否有可私有化部署且易于使用的PDF在线工具。大雄平时也喜欢制作PPT,每当有灵感时就会创建超过60多页的ppt演示文稿。 最近我在GitHub上闲逛时,恰好发现了一个名为Stirling-PDF的项目,该项目
hdu 7095 Add or Multiply 1 第二类Stirling数
https://acm.hdu.edu.cn/showproblem.php?pid=7095 给出若干个加法和乘法的操作次数,问有多少个本质不同的操作序列 比如说如果有两个加法和一个乘法,那么得到的操作序列可以是下面的几种 1 ◯ ( ( x + a 1 ) + a 2 ) × a 3 2 ◯ ( ( x + a 1 ) × a 3 ) + a 2 3 ◯ ( ( x + a 2 ) + a