rbtree专题

C++笔记19•数据结构:红黑树(RBTree)•

红黑树 1.简介：红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或 Black。通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。当搜索二叉树退化为单支树时，搜索效率极低，为了使搜索效率高，建立平衡搜索二叉树就需要"平衡树"来解决。上一篇博客介绍了AVL树，这

【C++进阶】RBTree封装map与set

1.红黑树的迭代器 1.1 begin() begin()就是红黑树的开头，那么对于红黑树来说按照中序序列是该树的最左节点。 Iterator Begin(){Node* leftMin = _root;while (leftMin->_left){leftMin = leftMin->_left;}return Iterator(leftMin);} 1.2 end() begin(

C++ RBTree封装mapset

目录 RBTreeNode的声明 RBTree结构 map结构 set结构改造红黑树迭代器类迭代器成员函数默认成员函数 Insert set map RBTreeNode的声明 template<class T>struct RBTreeNode{RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTree

红黑树（RBTree）认识总结

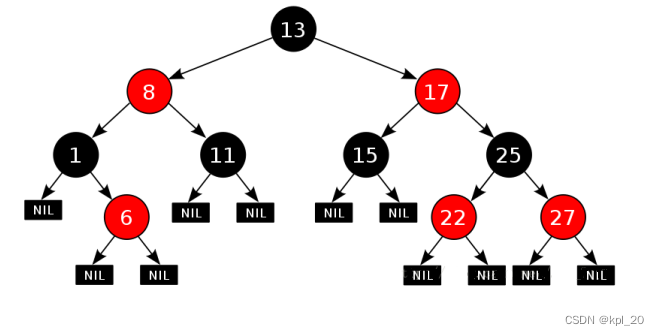
一、认识红黑树 1.1 什么是红黑树？红黑树是一种二叉搜索树，与普通搜索树不同的是，在每个节点上增加一个“颜色”变量 —— RED / BLACK 。通过对各个节点颜色的限制，确保从根到 NIL ，没有一条路径会比其他路径长出两倍。（NIL ：表示叶子节点的空指针，统一设置为 BLACK ） 1.2 红黑树的性质根节点一定是黑色不能出现两个连续的红色节点对于同一高度而言

数据结构-红黑树（RBTree）

红黑树是一棵二叉搜索树，它在每个节点上增加了一个存储位来表示节点的颜色，可以是Red或Black。通过对任何一条从根到叶子简单路径上的颜色来约束，红黑树保证最长路径不超过最短路径的两倍，因而近似于平衡。红黑树是满足下面红黑性质的二叉搜索树 1. 每个节点，不是红色就是黑色的 2. 根节点是黑色的 3. 如果一个节点是红色的，则它的两个子节点是黑色的

菜鸟nginx源码剖析数据结构篇（四）红黑树ngx_rbtree_t

分类： Server - 菜鸟nginx源码剖析 2014-10-27 21:17 9320人阅读评论(4) 收藏举报剖析源码 nginx 红黑树 c++ 目录(?)[+] 菜鸟nginx源码剖析数据结构篇（四）红黑树ngx_rbtree_t Author：Echo Chen（陈斌） Email：chenb19870707@gmai

[数据结构 - C++] 红黑树RBTree

文章目录 1、前言2、红黑树的概念3、红黑树的性质4、红黑树节点的定义5、红黑树的插入Insert6、红黑树的验证7、红黑树与AVL树的比较附录： 1、前言我们在学习了二叉搜索树后，在它的基础上又学习了AVL树，知道了AVL树是靠平衡因子来调节左右高度差，从而让树变得平衡的。本篇我们再来学习一个依靠另一种平衡规则来控制的二叉搜索树——红黑树。 2、红黑树的概念红黑树，是

『 C++ 』红黑树RBTree详解 ( 万字 )

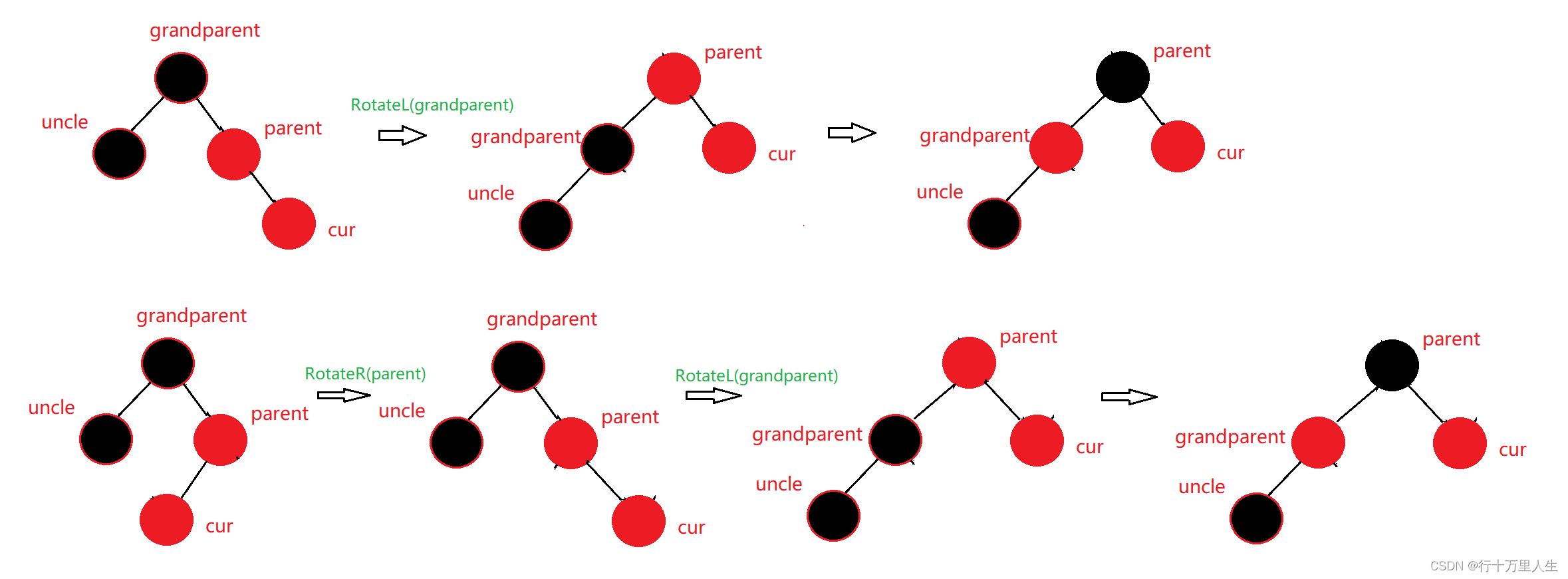
文章目录 🦖 红黑树概念🦖 红黑树节点的定义🦖 红黑树的插入🦖 数据插入后的调整🦕 情况一:ucnle存在且为红🦕 情况二:uncle不存在或uncle存在且为黑🦕 插入函数代码段(参考)🦕 旋转操作代码段(参考) 🦖 判断红黑树是否符合规则🦖 红黑树的析构函数🦖 完整代码(供参考) 🦖 红黑树概念红黑树是一棵较为复杂的树; 其与AVL树相同

【数据结构】模拟实现红黑树（RBTree）的插入算法

1、红黑树基本概念含义：首先红黑树是一棵二叉搜索树，它在每一个节点上增加了一个存储位来表示节点的颜色（red 或 black）。红黑树通过对任何一条从根节点到叶子节点简单路径上的颜色来约束，红黑树保证最长路径不超过最短路径的两倍，因而近似平衡，而且在实际应用中发现红黑树性能确实比AVL树性能高。【数据结构】二叉搜索树的插入，删除，查找等基本操作的实现【数据结构】AVL树的平衡化旋转

红黑树（RBTree）的插入算法以及如何测试一棵树是否是红黑树？（详细图解说明）

1.什么叫红黑树？红黑树是一棵二叉搜索树，它在每个节点上增加了一个存储位来表示节点的颜色，可以是Red或Black。通过对任何一条从根到叶子简单路径上的颜色来约束，红黑树保证最长路径不超过最短路径的两倍，因而近似于平衡。 2.红黑树的性质 1. 每个节点，不是红色就是黑色的 2. 根节点是黑色的 3. 如果一个节点是红色

set和map + multiset和multimap（使用+封装(RBTree)）

set和map 前言一、使用1. set(1)、模板参数列表(2)、常见构造(3)、find和count(4)、insert和erase(5)、iterator(6)、lower_bound和upper_bound 2. multiset3. map(1)、模板参数列表(2)、构造(3)、modifiers和operations(4)、operator[] 4. multimap 二、封装R

C++ RBTree 理论

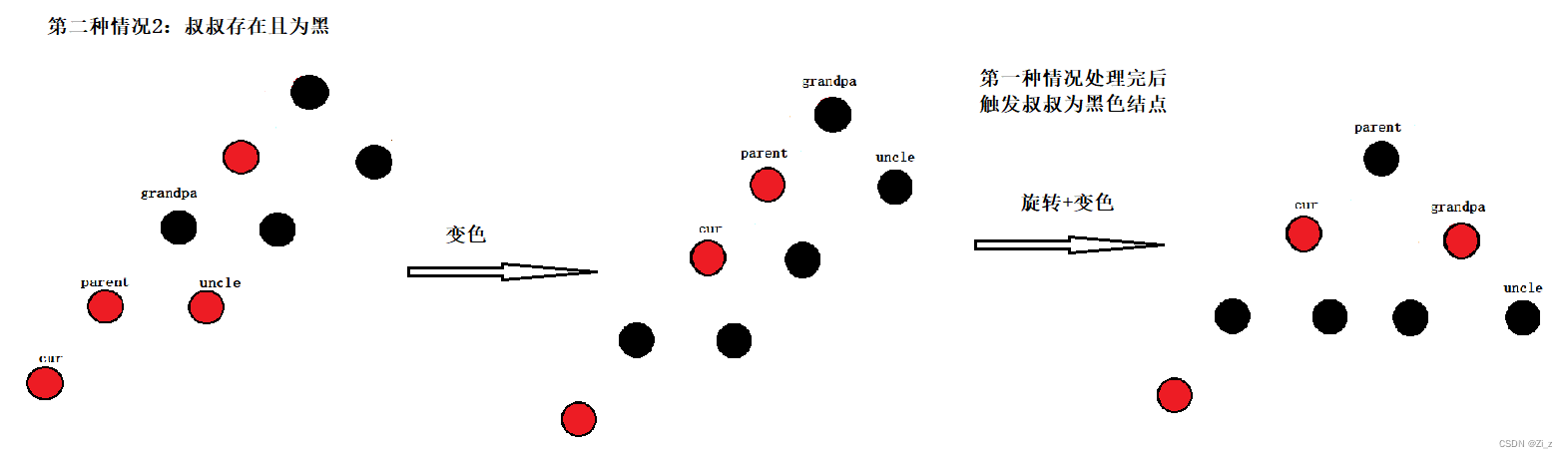
目录这个性质可以总结为红黑树的最短最长路径红黑树的路径范围 code 结构搞颜色类插入插入逻辑新插入节点思考：2. 检测新节点插入后，红黑树的性质是否造到破坏？解决方法变色旋转+变色第三种情况，如果根节点上面还有节点这个性质可以总结为 1.每个节点不是红色就是黑色 2.根节点是黑色的 3.不能有两个连续的红色节点

红黑树-RBTree

目录 1. 红黑树的概念2. 红黑树的性质3. 结点的定义4. 结点的插入5. 整体代码 1. 红黑树的概念红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。最短路径：全黑；最长路径：一黑一红交替。由于a

【C++杂货铺】一文带你走进RBTree

文章目录一、红黑树的概念二、红黑树的性质三、红黑树结点的定义四、红黑树的插入操作4.1 情况一：uncle 存在且为红4.2 情况二：uncle 不存在4.3 情况三：uncle 存在且为黑4.4 插入完整源码五、红黑树的验证六、红黑树与 AVL 树的比较七、结语一、红黑树的概念红黑树是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是 Red 或 B