permutations专题

LeetCode 46 Permutations + LeetCode 47 Permutations II

题意：给出一串（46题）不重复or（47题）有重复的数字，要求输出所有排列。思路：有没有重复不影响思路 = =。代码展示为46题提交结果，47题一样过…… 可以偷懒用next_permutation方法也可以自己实现，实现方法为从后往前找第一个出现的nums[i] < nums[i+1]，从i后面找出比nums[i]稍大一点的数字nums[x]，交换nums[i]和nums[

leetcode 刷题之路 12 Permutations

Given a collection of numbers, return all possible permutations. For example, [1,2,3] have the following permutations: [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], and [3,2,1]. 全排列问题，详细分析参考这篇文章

Leetcode94: Permutations

Given a collection of numbers, return all possible permutations. For example, [1,2,3] have the following permutations: [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], and [3,2,1]. 解题思路：字符交换加dfs。将第

46. Permutations, 47. Permutations II

Given a collection of distinct numbers, return all possible permutations. For example, [1,2,3] have the following permutations: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ] 无重复数

UVa 11077 Find the Permutations / 置换

把一个排列p变成1,2,...,n可以反过来看成1,2,...,n到p 把p分解乘循环如果一个循环有n个元素需要n-1次交换 dp[i][j] = dp[i-1][j] + dp[i-1][j-1] * (i-1); 代表i个元素交换j次变成1,2,...,n,的种数对于元素i 他可以自己成为一个循环那么交换次数不变种数+1 就是 dp[i-1][j]

codeforces 463D Gargari and Permutations

题意：从所给的序列中找出它们的最长公共子序列。思路： DAG（有向无环图）+BFS。如果数值 i 在所有序列中都在 j 前面。则i -> j连一条有向边。（好像还有个dp的思路的）参考：http://www.cnblogs.com/hujunzheng/p/3947392.html AC代码： #include <cstdio>#include <cstring>#i

leetcode之全排列问题(Permutations)

在leetcode上，跟Permutations有关的题目： 31 Next Permutation46 Permutations 一.31 Next Permutation 　　31题是排列的入门题，给出[1,2,3,4]，需给出下一排列[1,2,4,3]。这题有固定的解法，给定排序nums[n]=[1,4,2,7,6,5,3],n=0~6：从序号6开始往前寻找第一对严格递减（即找到第

Codeforces #264 (Div. 2) D. Gargari and Permutations

Gargari got bored to play with the bishops and now, after solving the problem about them, he is trying to do math homework. In a math book he have foundk permutations. Each of them consists of number

LeetCode Permutations II

Given a collection of numbers that might contain duplicates, return all possible unique permutations. For example, [1,1,2] have the following unique permutations: [1,1,2], [1,2,1], and [2,1,1]. 题

uva 11077 - Find the Permutations(置换)

题目链接：uva 11077 - Find the Permutations 题目大意：给定一个1~n的排序，可以通过一系列的交换变成1，2，…,n, 给定n和k，统计有多少个排列至少需要交换k次才能变成有序的序列。解题思路：给定一个序列P，可以将该序列看做是一个置换，从有序序列，开始，需要多少次回到有序序列。将P的循环分解，循环长度为1的需要0次，长度为2的需要1次，循环长度为n的需

Leetcode 046 Permutations

题目连接：Leetcode 046 Permutations 解题思路：用 Leetcode 031的方法，每次获取下一个序列。 class Solution {public:bool nextPermutation(vector<int>& nums) {int n = nums.size();int idx = n - 1;while (idx && nums[idx-1] >= nums

LeetCode 46. Permutations DFS

https://leetcode.com/problems/permutations/ 这道题没啥说的暴力DFS搞，也可以next_permutation #include <cstdio>#include <cstring>#include <algorithm>#include <iostream>#include <vector>using namespace

**Leetcode 47. Permutations II

https://leetcode.com/problems/permutations-ii/description/ 判重这里需要在注意判重只加一行代码就行了。道理很简单比如1有3个，那么visit中第一个1没访问过，就去用第二个1，这样其实就在构造重复解， class Solution {public:void dfs(vector<int>& nums, vector<int

99. Permutations

Given a collection of distinct numbers, return all possible permutations. For example, [1,2,3] have the following permutations: [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], and [3,2,1]. 分析: 采用从

144.Permutations II

Given a collection of numbers that might contain duplicates, return all possible unique permutations. For example, [1,1,2] have the following unique permutations: [[1,1,2],[1,2,1],[2,1,1]] 分析

leetcode46-Permutations

题目给定一个不含重复数字的数组 nums ，返回其所有可能的全排列。你可以按任意顺序返回答案。示例 1：输入：nums = [1,2,3] 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 分析求全排列，我们可以用递归的思路，反复交换第一个元素和其它元素的位置然后如果这个时候我们已经有了后面元素的全排列，那么这个数组的全

Leetcode: Permutations II

题目： Given a collection of numbers that might contain duplicates, return all possible unique permutations. For example,[1,1,2] have the following unique permutations:[1,1,2], [1,2,1], and [2,1,1].

Leetcode: Permutations

题目： Given a collection of numbers, return all possible permutations. For example,[1,2,3] have the following permutations:[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], and [3,2,1]. 思路分析：思路一：最

[leetcode] permutations的讨论

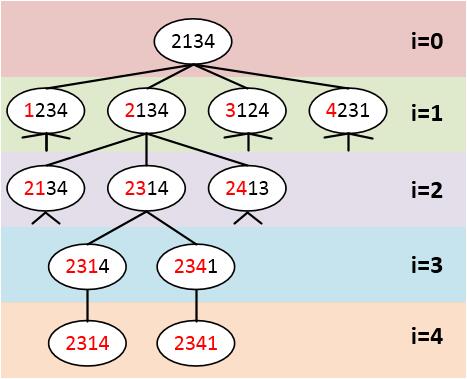
原题是找到一组数的全排列 Given a collection of numbers, return all possible permutations. For example, [1,2,3] have the following permutations: [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], and [3,2,1]. 函数原型

LeetCode--47. Permutations II

题目链接：https://leetcode.com/problems/permutations-ii/ 这个题目就是跟https://blog.csdn.net/To_be_to_thought/article/details/85126156这篇思路类似，就是在46. Permutations的基础上用HashSet进行去重操作。代码的逻辑结构基本一致： class Solution {pu

LeetCode--46. Permutations

题目链接：https://leetcode.com/problems/permutations/ 昨天是组合的题目，今天是排列问题，排列的题目就是对于每个元素在某个特定位置上到底选不选的问题。而在前面的位置上选了的某个元素在后面的位置上是不能选的。这时就需要一个全局数组visited来记录选了的与没选的情况。与组合一样，我会用一个ret来存储所有符合条件的排列情况最终返回，而用record数组记

codeforces1207D - Number Of Permutations

D. Number Of Permutations time limit per test2 seconds memory limit per test256 megabytes inputstandard input outputstandard output You are given a sequence of ? pairs of integers: (?1,?1),(?2,?2),…,(

习题 8-7 生成排列（Generating Permutations，UVa11925）

原题链接：https://vjudge.net/problem/UVA-11925 分类：构造法备注：思维题给一个数字n，和一个长度为n的排列，求如何操作使得1,2,…,n变成给定的排列。操作1为把前两个数交换位置，操作2为把第一个数放到最后。逆向操作，即把操作2改为把最后一个数放到前面，从给定的序列变成1,2,…,n的序列。按照一般想法，小的数在大的数前面，如果前两个数，前者更大则要交

「Positions in Permutations」Solution

简述题意给定 n , m n,m n,m，对于一个长度为 n n n 的排列 p p p，有函数： F ( p ) = ∑ i = 1 n [ ∣ p i − i ∣ = 1 ] F(p)=\sum_{i=1}^{n}[\left|p_i-i\right|=1 ] F(p)=i=1∑n[∣pi−i∣=1]求有多少个排列满足 F ( p ) = m F(p) = m F(p)=m，答

2019牛客暑期多校训练营（第九场）C Inversions of all permutations

This way 题意：给你一个数组a，设r为a的某种排序， t ( r ) t(r) t(r)为r中逆序对的个数，问你 ∑ b t ( r ) \sum{b^{t(r)}} ∑bt(r)是多少题解：值不重复的时候，我们考虑第i大的数，它和前面i-1个数组成的逆序对的所有可能是0-（i-1）那么答案就乘上 ( 1 + b + b 2 + . . . + b i − 1 ) (1+b

let 46 Permutations

Given a collection of distinct numbers, return all possible permutations.For example,[1,2,3] have the following permutations:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 主题思想：就是排列排列算法，已经知道