leetcode之全排列问题(Permutations)

本文主要是介绍leetcode之全排列问题(Permutations)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在leetcode上，跟Permutations有关的题目：

31 Next Permutation
46 Permutations

一.31 Next Permutation

　　31题是排列的入门题，给出[1,2,3,4]，需给出下一排列[1,2,4,3]。这题有固定的解法，给定排序nums[n]=[1,4,2,7,6,5,3],n=0~6：

从序号6开始往前寻找第一对严格递减（即找到第一个小于的数，从后往前看）的两个数，在这里是[2,7]，记作[i,j]，从7→2是严格递减。
从序号6开始寻找第一个大于序号i的数2，找到数3序号k，交换数2序号i和数3序号k，得到[1,4,3,7,6,5,2]
将从j开始（从7开始）一直到最后的序列改为正序（此时的序列一定是逆序的），得到[1,4,3,2,5,6,7]

这里考虑两种极端情况[1,2,3,4,5,6,7]和[7,6,5,4,3,2,1]。
　　前一种情况：[i,j]=[6,7]，[k]=[7]；交换i,k，即6和7；反转从k开始的序列，这种情况不特殊，可与一般情况的一起处理；
　　后一种情况：i<0,j=0，直接全体逆序一下即可，这种情况特殊，不能和一般情况一起处理。

二.46 Permutations

本题可以有三种解法：

回溯法（此方法也是leetcode上提示的方法）
利用31题，只要知道一种排列，后续的都可以next出来
使用dfs

2.1 回溯法

　　回溯法的本质是类似于枚举的搜索尝试过程，一般都带着条件去搜索，如果发现继续搜索下去也找不到最优解，那么在此点就开始回溯。一般我们将它的解空间转化转化为树的形式，这样便于理解。
　　这里我们以排序[1,2,3,4]为例，画出它的解空间树。每当i=4的时候，说明已经找到了一个解。需要寻找下一个解。比如找到了第4层的2314后，这时已经到头了，我们需要回溯，返回到第3层，再返回到第2层的2314，然后沿着另外一条路到了第4层的2341，这样就找到了另一个解。
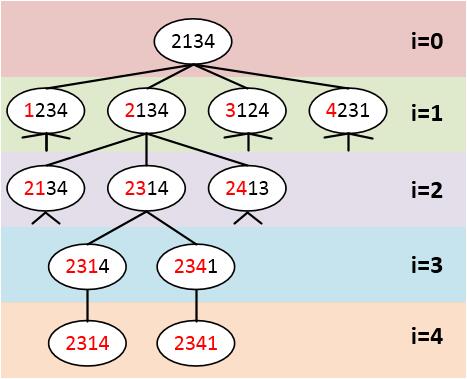
这里写图片描述
　　在排列问题中，没有约束条件，没有约束条件的回溯有点像暴力穷举，要达到叶子结点才会回溯。如要有条件的话，就可以对解空间树进行剪枝，可以避免许多明显不必要搜索的路径。
　　用递归实现的回溯比较简单易懂，回溯法一般有以下模板：

//用递归实现回溯的一般模板
void backTrack(int i) {if(i > n) {//到达叶子结点，分析此解是否最优return;}for(int k=low; k<high; k++) {if(fx()) {//满足约束条件a += nums[i];backTrack(i+1);a -= nums[i];//在回溯前进行状态的清零}}
}

　　有许多经典的问题都可以用回溯法来解决，比如8皇后问题、01背包问题等。
　　回归这道题目，下面给出这道题回溯解法。

public class Solution {public List<List<Integer>> permute(int[] nums) {List<List<Integer>> arrAll = new ArrayList<List<Integer>>();backTrack(0, nums, arrAll);return arrAll;}private void backTrack(int i, int[] nums, List<List<Integer>> arrAll) {if(i>=nums.length) {List<Integer> arr = new ArrayList<Integer>();for (int a : nums) {arr.add(a);}arrAll.add(arr);return;}for(int k=i; k<nums.length; k++) {exch(nums, i, k);backTrack(i+1, nums, arrAll);exch(nums, i, k);}}private void exch(int[] nums, int i, int k) {int temp = nums[i];nums[i] = nums[k];nums[k] = temp;}
}