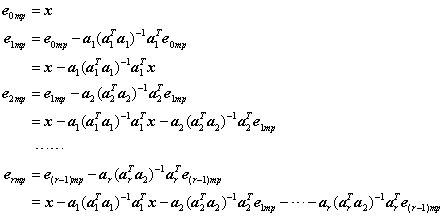omp专题
【darknet】源码阅读理解(四)——#pragma omp parallel for
参考自:https://www.cnblogs.com/qinguoyi/p/7251305.html 出处: darknet在cpu上进行CNN计算时。 Code: void gemm_nn(int M, int N, int K, float ALPHA, float *A, int lda, float *B, int ldb,float *C, int ldc){int i,j,k
小波包变换(WPT)和OMP实现压缩感知
压缩感知(Compressed Sensing)是一种信号处理理论,它可以从非常少量和不完整的采样中恢复信号,并且在图像处理、医学成像、通信等领域有着广泛的应用。下面是压缩感知算法的一般实现步骤和细节: 1. 压缩感知基本原理 压缩感知的基本思想是,信号通常具有一种稀疏性或者低复杂度性质,即它们的表示可以通过较少的系数来描述。基于这个原理,压缩感知假设信号可以用一个稀疏变换域(如小波变换、稀疏
使用OMP复原一维信号(MATLAB)
参考文献 https://github.com/aresmiki/CS-Recovery-Algorithms/tree/master MATLAB代码 %% 含有噪声% minimize ||x||_1% subject to: (||Ax-y||_2)^2<=eps;% minimize : (||Ax-y||_2)^2+lambda*||x||_1% y传输中可能含噪 y
包含密钥的OMP压缩感知模拟(MATLAB)
压缩感知(Compressed Sensing,CS)是一种新颖的信号采样和重建理论,它通过利用信号的稀疏性或者低维性,从极少量的观测中直接重建出完整的信号。压缩感知的核心思想是,在合适的条件下,信号本身的稀疏性或低维性可以使其信息内容大幅减少,从而可以通过较少的观测数据进行采样和重建,从而实现了信号的高效压缩和重构。 下面是压缩感知的主要原理和关键步骤: 稀疏表示:压缩感知的第一步是假设信
OMP实现压缩感知的实现(MATLAB)
本文介绍通过DWT和OMP实现压缩感知。 不同的是,将DWT得到的低频放到了作为稀疏矩阵的顶部。 压缩感知 压缩感知算法是一种用于从高维度数据中恢复稀疏信号的方法。它通常用于处理信号的采样和重建,例如图像或音频。以下是压缩感知算法的一般实现细节: 信号表示: 压缩感知算法假设信号是稀疏的,即在某个合适的基下,信号的表示具有少量的非零系数。例如,在图像中,许多像素可能是零,或者在音频中,许多
MATLAB使用OMP实现图像的压缩感知实例
OMP(Orthogonal Matching Pursuit)是一种用于稀疏信号恢复的迭代算法。它的目标是从一组测量值中重建具有少量非零元素的信号。 基本步骤 以下是OMP算法的简要步骤: 初始化残差: 将残差初始化为测量向量。 迭代过程: a. 原子选择: 在每次迭代中,从字典中选择与当前残差最相关的原子。 b. 更新估计: 使用所选的原子更新信号的估计。 c. 更新残差: 更新残差
OMP实现MATLAB压缩感知实例
OMP(Orthogonal Matching Pursuit,正交匹配追踪)算法是一种用于稀疏信号重构的迭代算法。它的基本思想是在每一步选择与当前残差最相关的原子(或基),并使用它来更新估计值,直到满足停止准则为止。 基本流程 下面是OMP算法的基本流程: 初始化: 将残差初始化为原始信号。将估计的稀疏系数集合初始化为空。 迭代步骤: 选取原子:从未被选取的原子集合中选择与当前残差的内
用买糖果的方式来理解正交匹配追踪(OMP)算法
在信号处理领域,压缩感知(Compressed Sensing)是一种能够从远少于传统奈奎斯特采样定理所要求的样本数目中重建稀疏信号的技术。压缩感知的理论基础在于一个前提假设,即许多自然信号都含有稀疏的表示,换句话说,这些信号可以用很少的非零系数表达。在这个框架下,贪婪算法,如匹配追踪(Matching Pursuit, MP)和正交匹配追踪(Orthogonal Matching Pursuit
图像压缩感知的MATLAB实现(OMP)
前面实现了 压缩感知的图像仿真(MATLAB源代码) 效果还不错,缺点是速度慢如牛。 下面我们采用OMP对其进行优化,提升速度。具体代码如下: 仿真 构建了一个MATLAB文件,所有代码都在一个源文件里面: MATLAB实现 clcclearvars;%------------ 读取图像 --------------img=imread('lenagray.bmp'); % 测试
正交匹配追踪(Orthogonal Matching Pursuit, OMP)的MATLAB实现
压缩感知(Compressed Sensing, CS)是一种利用稀疏信号的先验知识,用远少于奈奎斯特采样定理要求的样本数目恢复整个信号的技术。正交匹配追踪(Orthogonal Matching Pursuit, OMP)是一种常见的贪婪算法(Greedy algorithm),用于解决压缩感知中的信号重构问题。OMP算法试图找到一组稀疏基,这些基与测量值之间有最大的相关性,并且用于迭代地重构原
【图像修复】OMP算法图像修复【含Matlab源码 3465期】
⛄一、OMP算法图像修复 1 前言 在实际应用中,我们的图像常常会被噪声腐蚀,这些噪声或是镜头上的灰尘或水滴,或是旧照片的划痕,或者是图像遭到人为的涂画(比如马赛克)或者图像的部分本身已经损坏。 2 图像修复技术的原理 简而言之,就是利用那些已经被破坏的区域的边缘, 即边缘的颜色和结构,根据这些图像留下的信息去推断被破坏的信息区的信息内容,然后对破坏区进行填补 ,以达到图像修补的目的。 第
pytorch实现多进程的时候出现的BUG:OMP: Error #13: Assertion failure at z_Linux_util.cpp(2361).
在跑强化学习A3C的代码时候,用到python和pytorch的多进程,但是遇到这样的bug。 OMP: Error #13: Assertion failure at z_Linux_util.cpp(2361).
压缩感知OMP(正交匹配追踪法 Orthogonal Matching Pursuit) 算法python实现
论文原文: % Signal Recovery From Random Measurements Via Orthogonal Matching % Pursuit,IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 53, NO. 12 实现代码: def cs_omp(y,Phi,N,K): residual=y #初始化残差index
Python杂谈 | (12) OMP: Error #15: Initializing libiomp5.dylib, but found libiomp5.dylib already initia
调程序时遇到问题 OMP: Error #15: Initializing libiomp5.dylib, but found libiomp5.dylib already initialized. 加上以下两行就好了: import osos.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"
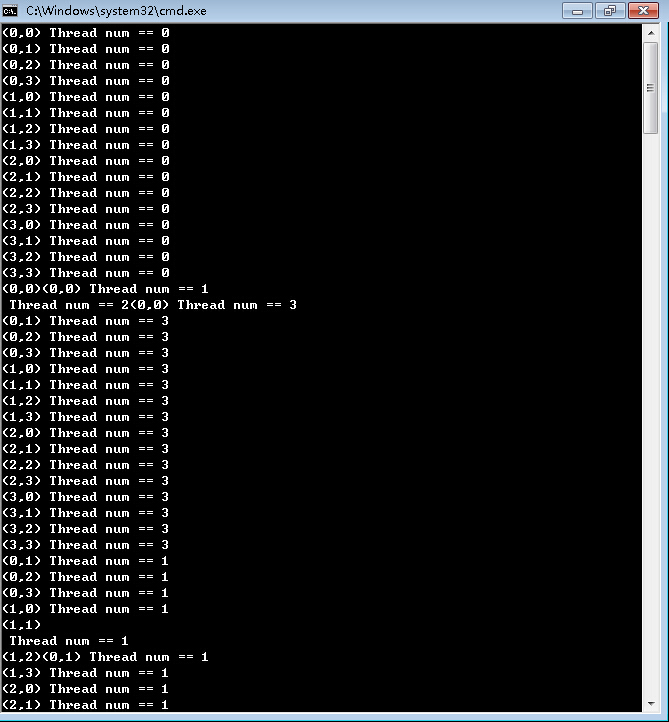
OpenMP #pragma omp parallel for并行化小探究
今天用了一下openmp,本人表示非常喜欢openmp的傻瓜化模式,导入一个头文件 直接parallel for #include <iostream>#include <omp.h>using namespace std;int main(){//cout<<"Thread num == "<<omp_get_thread_num()<<endl;#pragma omp parallel
linux怎么运行omp,在Linux系统上进行openmp多线程编程的方法
OpenMP是一种多处理器多线程的编程语言,能够支持多个平台,包括Linux系统,那么Linux下要如何进行openmp多线程编程呢?一起来了解下吧。 关键语法: 代码如下: #inlcude 《omp.h》 #pragma omp parallel for #pragma omp for reduction(+: 变量) #pragma omp critical//锁 { } #pragma
【转载】稀疏分解中的MP与OMP算法
转自https://blog.csdn.net/wwf_lightning/article/details/70142985 MP:matching pursuit匹配追踪 OMP:正交匹配追踪 主要介绍MP与OMP算法的思想与流程,解释为什么需要引入正交? !!今天发现一个重大问题,是在读了博主的正交匹配追踪(OMP)在稀疏分解与压缩感知重构中的异同,http:/
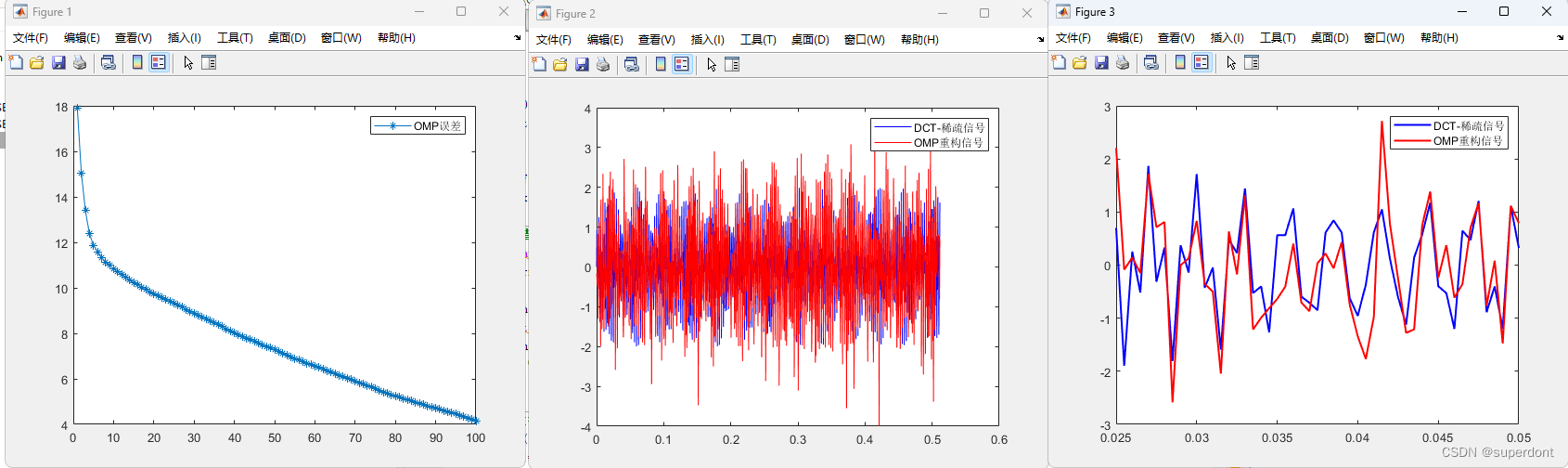
压缩感知重构算法之正交匹配追踪(omp)及其matlab实现
压缩感知之OMP恢复算法 1、基本思想 y=Φx x=Ψθ 正交匹配追踪算法的本质思想是,以贪婪迭代的方式选择测量矩阵Φ的列,使得在每次迭代中所选择的列与当前的冗余向量最大程度地相关,从测量向量中减去相关部分并反复迭代,直到迭代次数达到稀疏度K,强制迭代停止。 2、算法步骤 输入:(1)M*N的感知矩阵A,其中M远远小于N,A=Φ*Ψ。 (2)长度为M的数据向