nmf专题
【Python机器学习】NMF——将NMF应用于人脸图像
将NMF应用于之前用过的Wild数据集中的Labeled Faces。NMF的主要参数是我们想要提取的分量个数。通常来说,这个数字要小于输入特征的个数(否则的话,将每个像素作为单独的分量就可以对数据进行解释)。 首先,观察分类个数如何影响NMF重建数据的好坏: import mglearn.plotsimport numpy as npimport matplotlib.pyplot as
文本挖掘之降维技术之特征抽取之非负矩阵分解(NMF)
通常的矩阵分解会把一个大的矩阵分解为多个小的矩阵,但是这些矩阵的元素有正有负。而在现实世界中,比如图像,文本等形成的矩阵中负数的存在是没有意义的,所以如果能把一个矩阵分解成全是非负元素是很有意义的。在NMF中要求原始的矩阵的所有元素的均是非负的,那么矩阵可以分解为两个更小的非负矩阵的乘积,这个矩阵 有且仅有一个这样的分解,即满足存在性和唯一性。 Contents
非负矩阵分解(NMF)
转载自: http://blog.csdn.net/pipisorry/article/details/52098864 非负矩阵分解(NMF,Non-negative matrix factorization) NMF的发展及原理 著名的科学杂志《Nature》于1999年刊登了两位科学家D.D.Lee和H.S.Seung对数学中非负矩阵研究的突出成果。该文提出了一种新的矩阵分解思想——
【Python机器学习】NMF——模拟数据
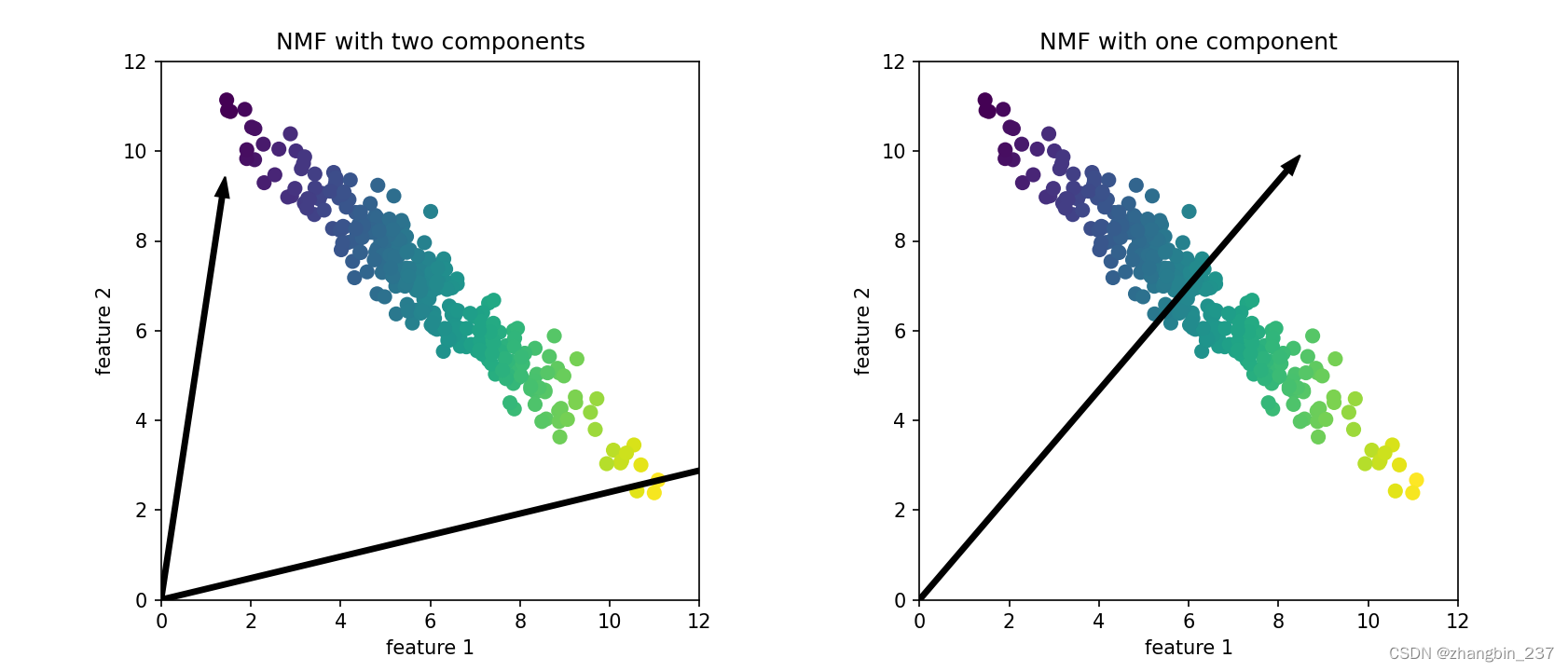
与使用PCA不同,我们需要保证数据是正的,NMF能够对数据进行操作。这说明数据相对于原点(0,0)的位置实际上对NMF很重要。因此,可以将提取出来的非负向量看作是从(0,0)到数据的方向。 举例:NMF在二维玩具数据上的结果: import mglearn.plotsimport matplotlib.pyplot as pltmglearn.plots.plot_nmf_illustrat
NMF(non-negative matrix factorization)相关论文[1]
部分非负矩阵分解论文的总结,在做相关工作的童鞋的可以互相交流下~! Guan N, Tao D, Luo Z, et al. Online non-negative matrix factorization with robust stochastic approximation[J]. IEEE Transactions on Neural Networks & Learning Syste
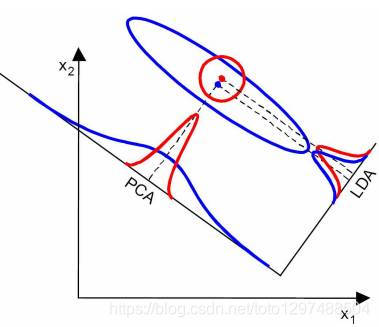
07_数据降维,降维算法,主成分分析PCA,NMF,线性判别分析LDA
1、降维介绍 保证数据所具有的代表性特性或分布的情况下,将高维数据转化为低维数据。 聚类和分类都是无监督学习的典型任务,任务之间存在关联,比如某些高维数据的分类可以通过降维处理更好的获得。 降维过程可以被理解为数据集的组成成分进行分解(decomposition)的过程,因此sklearn为降维模块命名为decomposition。在对降维算法调用需要使用sklearn.decomposit
线性代数 NMF 非负矩阵分解 Matlab
点乘 dot product A.*B 叉乘 cross product A*B 转置 tranpose A' 记为A的转置 点除 dot divide A./B 举例 矩阵 A 为 矩阵B为 C=A*B=×==



![NMF(non-negative matrix factorization)相关论文[1]](https://img-blog.csdn.net/20170512153946221?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvdTAxMDEzODA1NQ==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast)