multiplication专题

[论文笔记]LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale

引言今天带来第一篇量化论文LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale笔记。为了简单，下文中以翻译的口吻记录，比如替换"作者"为"我们"。大语言模型已被广泛采用，但推理时需要大量的GPU内存。我们开发了一种Int8矩阵乘法的过程，用于Transformer中的前馈和注意力投影层，这可以将推理所需

杭电1082Matrix Chain Multiplication

杭电1082Matrix Chain Multiplication 这道题看oj上评论说很水，可是自己居然想了几个小时，看来对栈的的操作还是不够清晰熟练啊。总体思路就是把先把括号里面的表达式，然后再依次向外消掉括号。我的思路就是把（AB（AA（A）））（A（AB）），先运算成（#（#（#）））（#（#）），然后把这个压入数组中，然后遇到‘）’我们就对数组中的倒数第二个和倒数第

HDU 1517 A Multiplication Game 巴什博弈

题意：2 个人玩游戏，给定一个数n,从 1 开始，轮流对数进行累乘一个数（2~9中取），直到第一次等于或超过n为赢. 思路：1)找规律如果n是 2 ~ 9 ，Stan 必胜。如果输入是 10~18 ，不管第一次Stan 乘的是什么，Stan肯定在 2 ~ 9 之间，无论stan乘以什么，Ollie乘以大于1的数都都能超过 10 ~ 18 中的任何一个数。Ollie 必胜

从行或列的角度思考矩阵-向量乘法（matrix-vector multiplication）

从行或列的角度思考矩阵-向量乘法可以帮助理解这个运算的几何意义以及如何在计算中操作。 1. 从行的角度思考假设我们有一个 m × n m \times n m×n的矩阵 A A A 和一个 n × 1 n \times 1 n×1的列向量 x \mathbf{x} x。矩阵-向量乘法 A x A\mathbf{x} Ax 的结果是一个 m × 1 m \times 1 m×1的列

poj3318--Matrix Multiplication（随机算法）

题目链接：点击打开链接题目大意：给出三个n*n矩阵的矩阵a，b，c问a*b是否等于c，等于输出YES，否则输出NO n的最大值是500，计算矩阵乘法的话需要O(n^3)的复杂度，很明显超时。随机出一列k，计算a*(b*k) 和c*k，计算出一列的值，这样的如果a*b==c那么a*(b*k) 和c*k也一定会相等的，因为是随机的数，所以可以多测试几次。 #include <cstdi

codeforces#256DIV2 D题Multiplication Table

题目地址：http://codeforces.com/contest/448/problem/D 当时是按照找规律做的，规律倒是找出来了，但是很麻烦很麻烦。。看到前几名的红名爷们3分钟就过了，于是果断放弃了。。赛后才知道是用二分的方法做，知道了二分之后，剩下的就很简单了。。关键在于能不能想到用二分。。代码如下： #include <iostream>#include <stdio.h

HDU 4920 Matrix multiplication

Problem Description Given two matrices A and B of size n×n, find the product of them. bobo hates big integers. So you are only asked to find the result modulo 3. Input The input consist

Codeforces Round #256 (Div. 2) D. Multiplication Table

Bizon the Champion isn't just charming, he also is very smart. While some of us were learning the multiplication table, Bizon the Champion had fun in his own manner. Bizon the Champion painted an n

hdu 4920 Matrix multiplication(高效)

题目链接：4920 Matrix multiplication 题目大意：给定两个n阶矩阵，求矩阵相乘后模3. 解题思路：因为矩阵模掉3后只有0，1，2三种情况。所以对于矩阵A，记录每一行中1，2的位置，借助bitset。矩阵B中每一列1，2的位置。然后对于结果中每个位置，只要考虑1∗1,1∗2,2∗1，2∗2的个数即可。 #include <cstdio>#include <cst

Optimal Array Multiplication Sequence UVA - 348 (最优矩阵链乘+递归输出路径+区间dp)

题目链接：https://vjudge.net/problem/19208/origin 题目大意：对于一个a*b和b*c的矩阵相乘的结果为a*b*c，如果有三个矩阵相乘就是a*b b*c c*d 这三个矩阵相乘，因为满足结合律，所以可以先乘后两个，再和第一个相乘。由于先乘那一对矩阵决定了运算量的大小，所以让你计算怎么结合相乘能使得运算量最小。那么什么是运算量的大小呢：比如有三个矩阵为

向量、矩阵乘法的几何意义（一） scalar multiplication VS scalar product

1、scalar multiplication 纯量乘法（1）定义：纯量乘法是指一个标量r与一个向量V（或矩阵M）相乘，其结果为一个向量（矩阵），该向量（矩阵）的每一个元素为标量r与V（M）中对应位置元素的乘积。（2）几何意义： Scaling：对向量（矩阵）各维上的伸（stretch, r>1）缩（shrink, 0<r<1）。Scalar multiplica

Matrix Multiplication

Algorithm 2 —— Strassen’s algorithm Idea The idea behind this algorithm consists in reducing the number of multiplications at the expense of increasing the number of additions and subtr

ZOJ 1094_Matrix Chain Multiplication

大意：输入一系列矩阵（不超过26个），判断下面输入的矩阵乘法是否合法（即是否满足前者的列等于后者的行），若合法则输出其做了多次数的乘法运算（若有两矩阵A：a,b; B: b,c ,则其做的数乘法次数为a*b*c），若不合法，则输出error。分析：为了操作方便定义一个矩阵结构，保存矩阵名，row和column. 从题意可知，每次的乘法都用括号隔开，那么这里就符合LIFO。前括号可以忽略，

C#，数值计算，矩阵相乘的斯特拉森（Strassen’s Matrix Multiplication）分治算法与源代码

Volker Strassen 1 矩阵乘法矩阵乘法是机器学习中最基本的运算之一，对其进行优化是多种优化的关键。通常，将两个大小为N X N的矩阵相乘需要N^3次运算。从那以后，我们在更好、更聪明的矩阵乘法算法方面取得了长足的进步。沃尔克·斯特拉森于1969年首次发表了他的算法。这是第一个证明基本O（n^3）运行时不是optiomal的算法。 Strassen算法的基本思想是将A和B分

UVa 348 Optimal Array Multiplication Sequence (区间DP矩阵链乘,MCM)

348 - Optimal Array Multiplication Sequence Time limit: 3.000 seconds http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=24&page=show_problem&problem=284 记忆化搜索：dp[a]

668. Kth Smallest Number in Multiplication Table

花花酱 class Solution {public:int findKthNumber(int m, int n, int k) {int l = 1, r = m*n;while(l < r){int mid = l + (r -l)/2;if(les(m, n, mid) >= k) r = mid;else l = mid + 1;}return l;}int les(int m, i

UVA-442 Matrix Chain Multiplication

题目链接：https://vjudge.net/problem/UVA-442 题意：输入n个矩阵的维度和一些矩阵链乘表达式，输出乘法的次数。若乘法无法进行，输出error。假定A是m*n矩阵，B是n*p矩阵，那么AB是n*p矩阵，乘法次数为m*n*p。若A的列数不等于B的列数，则乘法无法进行。分析：用栈即可求出结果，遇到字母入栈，遇到右括号出栈并计算，结果入栈。 #include <

POJ 2955 Brackets POJ 1505 Copying Books POJ 1651 Multiplication Puzzle(初级区间DP)

POJ 2955 Brackets 题目大意在给定字符串中有多少个可匹配括号，()和[]为可匹配。解题思路 dp[i][j]代表i~j有多少个可匹配的字符串。转移方程： 1、dp[i][j]=dp[i+1][j-1]+2，当i,j位置组成可匹配括号； 2、枚举分割点k (i≤k<j) (i \le k<j) ：dp[i][j]=max(dp[i][j],dp[i][k]+dp

ML：2-1-5 matrix multiplication矩阵乘法

文章目录 1. 为什么neural network如此高效2. matrix multiplication（补充）3. matrix multiplication的规则（补充）4. matrix multiplication的代码（optional）【吴恩达p56-59】 1. 为什么neural network如此高效 neural network可以向量化，非常有效的

博弈--类似Bash--hdu1517 A Multiplication Game

给定n，初始p = 1，2人轮流乘上2-9的数，使p >= n时游戏结束。类似于Bash博弈（一共m个，每次取1-k个，除第一次外，2人都是1，k，1，k的取）除开始外，2人的最佳策略应该都是*2 ,*9,*2,*9循环。 #include <iostream> #include <cstdio> using namespacestd; int main

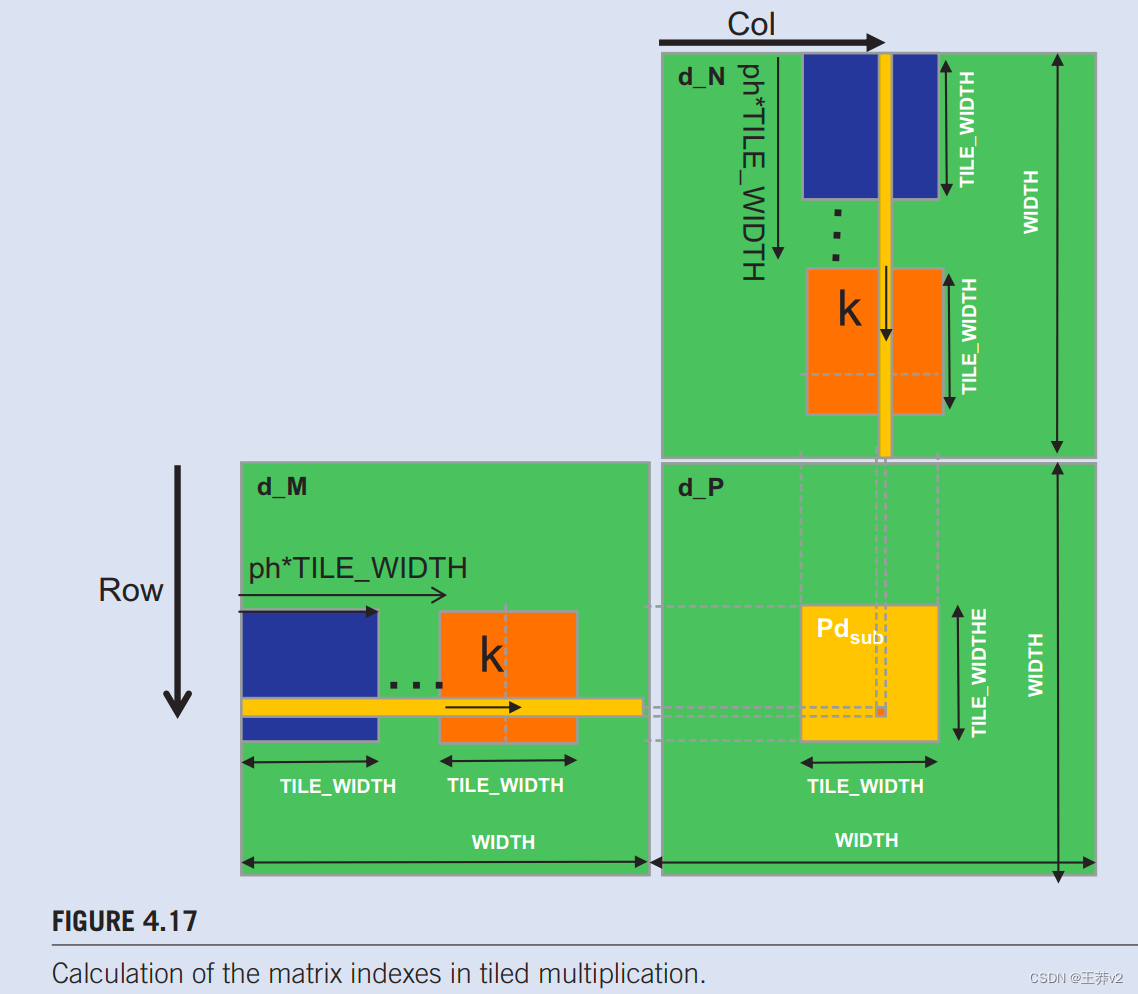
4.5 A TILED MATRIX MULTIPLICATION KERNEL

我们现在准备展示一个tiled矩阵乘法内核，该内核使用共享内存来减少对全局内存的流量。图中4.16显示的内核。实施图4.15.中所示的阶段。在图4.16中，第1行和第2行声明Mds和Nds为共享内存变量。回想一下，共享内存变量的范围是一个块。因此，将为每个块创建一对Mds和Nds，并且一个块的所有线程都可以访问相同的Mds和Nds。这很重要，因为块中的所有线程都必须能够访问加载的M和N元素由同行进

POJ 3673 Cow Multiplication

一、题目信息 Cow Multiplication Time Limit: 1000MS Memory Limit: 65536KTotal Submissions: 10216 Accepted: 6993 Description Bessie is tired of multiplying pairs of numbers the usual way, so she

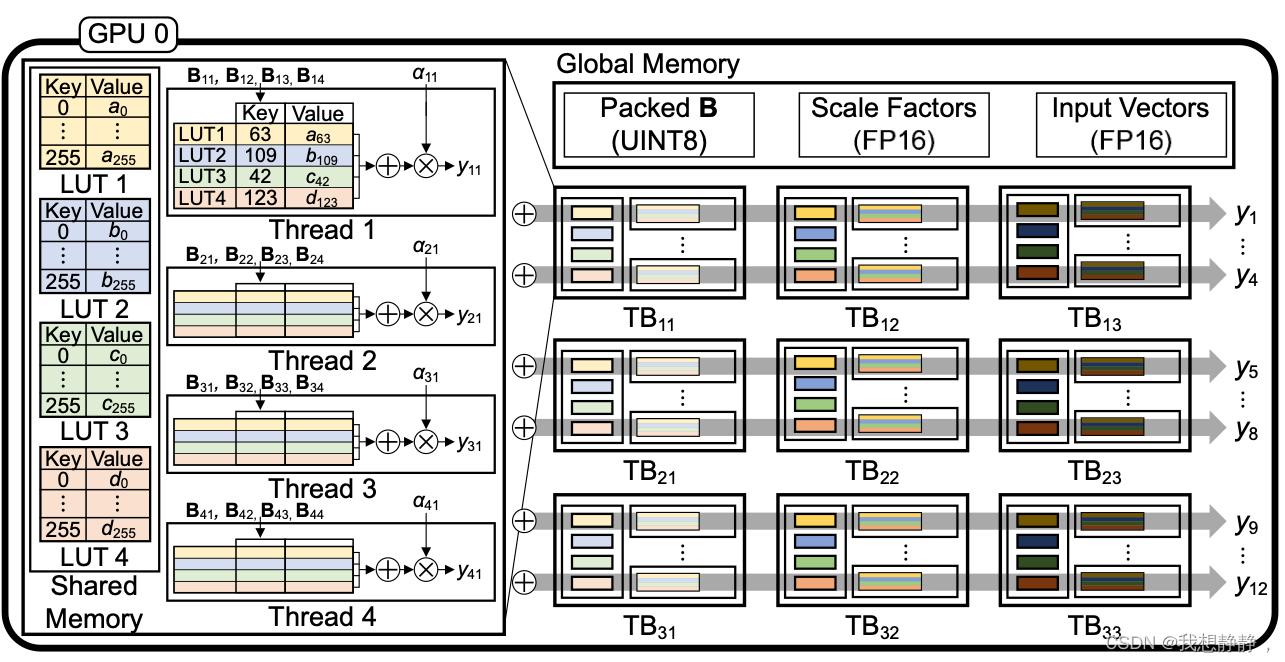
LUT-GEMM: Quantized Matrix Multiplication based on LUTs for Efficient Inference in Large-Scale Gener

文章目录 abstractintroduction背景量化二值量化BCQ LUT-GEMM二值量化扩展Group-wise 𝛼分配基于LUT的量化矩阵乘法LUT-GEMM内存占用实验Simple Comparisons with Various KernelsComparison with FP16 Tensor ParallelismExploration of Compressio

Tiled Matrix Multiplication

if(true) { (function(i,s,o,g,r,a,m){i[‘GoogleAnalyticsObject’]=r;i[r]=i[r]||function(){ (i[r].q=i[r].q||[]).push(arguments)},i[r].l=1*new Date();a=s.createElement(o), m=s.getElementsByTagName(o)[0];a.

uva 348 Optimal Array Multiplication Sequence

题意：给你n个矩阵，要你计算矩阵乘的最少运算量。 #include <iostream>#include <cstdio>#include <cstring>using namespace std;const int N=12;struct node{int x,y;}m[N];int map[N][N],ileft[N],iright[N];int dp(int,int)

LintCode 654 · Sparse Matrix Multiplication (稀疏矩阵乘法)

654 · Sparse Matrix Multiplication Algorithms Description Given two Sparse Matrix A and B, return the result of AB. You may assume that A’s column number is equal to B’s row number. Example Example