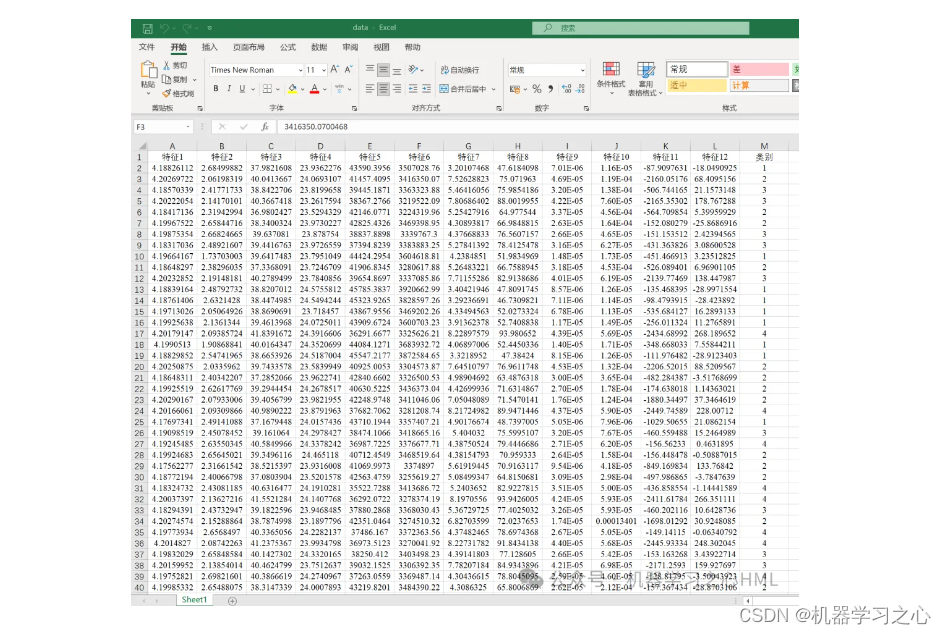
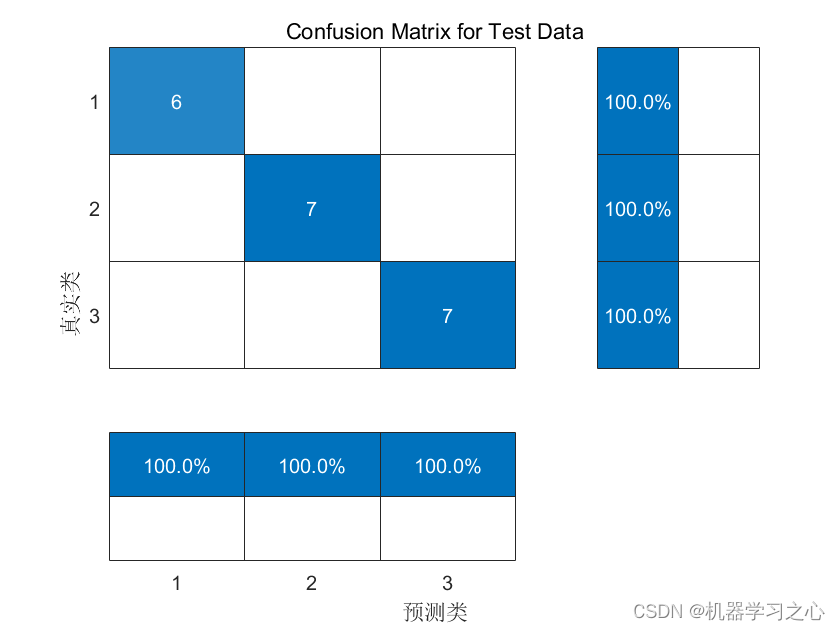
JCR一区级 | Matlab实现TCN-BiGRU-MATT时间卷积双向门控循环单元多特征分类预测 目录 JCR一区级 | Matlab实现TCN-BiGRU-MATT时间卷积双向门控循环单元多特征分类预测分类效果基本介绍程序设计参考资料 分类效果 基本介绍 1.Matlab实现TCN-BiGRU-MATT时间卷积双向门控循环单元多特征分类预测，T

JCR一区级 | Matlab实现TCN-LSTM-MATT时间卷积长短期记忆神经网络多特征分类预测 目录 JCR一区级 | Matlab实现TCN-LSTM-MATT时间卷积长短期记忆神经网络多特征分类预测分类效果基本介绍程序设计参考资料 分类效果 基本介绍 1.JCR一区级 | Matlab实现TCN-LSTM-MATT时间卷积长短期记忆神经网络多

JCR一区 | Matlab实现1D-2D-GASF-CNN-BiLSTM-MATT的多通道输入数据分类预测 目录 JCR一区 | Matlab实现1D-2D-GASF-CNN-BiLSTM-MATT的多通道输入数据分类预测分类效果基本介绍程序设计参考资料 分类效果 基本介绍 Matlab实现1D-2D-GASF-CNN-BiLSTM-MATT的多

JCR一区 | Matlab实现1D-2D-GASF-CNN-GRU-MATT的多通道输入数据分类预测 目录 JCR一区 | Matlab实现1D-2D-GASF-CNN-GRU-MATT的多通道输入数据分类预测分类效果基本介绍程序设计参考资料 分类效果 基本介绍 基本介绍 Matlab实现1D-2D-GASF-CNN-GRU-MATT的多通

EI级！高创新原创未发表！VMD-TCN-BiGRU-MATT变分模态分解卷积神经网络双向门控循环单元融合多头注意力机制多变量时间序列预测（Matlab） 目录 EI级！高创新原创未发表！VMD-TCN-BiGRU-MATT变分模态分解卷积神经网络双向门控循环单元融合多头注意力机制多变量时间序列预测（Matlab）预测效果基本介绍程序设计参考资料 预测效果

多维时序 | Matlab实现GRU-MATT门控循环单元融合多头注意力多变量时间序列预测模型 目录 多维时序 | Matlab实现GRU-MATT门控循环单元融合多头注意力多变量时间序列预测模型预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.多维时序 | Matlab实现GRU-MATT门控循环单元融合多头注意力多变量时间序列预测模型（完整源码

多维时序 | Matlab实现BiLSTM-MATT双向长短期记忆神经网络融合多头注意力多变量时间序列预测模型 目录 多维时序 | Matlab实现BiLSTM-MATT双向长短期记忆神经网络融合多头注意力多变量时间序列预测模型预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.多维时序 | Matlab实现BiLSTM-MATT双向长短期记忆神经

分类预测 | Matlab实现GAF-PCNN-MATT格拉姆角场和双通道PCNN融合多头注意力机制的分类预测/故障识别 目录 分类预测 | Matlab实现GAF-PCNN-MATT格拉姆角场和双通道PCNN融合多头注意力机制的分类预测/故障识别分类效果基本描述程序设计参考资料 分类效果 基本描述 1.Matlab实现GAF-PCNN-MATT格拉姆角

思路： （1）条件及问题：给定N个数，找到异或值大于等于M的总方案数； （2）分析： 可以dfs（）枚举，超时；考虑dp,dp[i][j]描述在前i个数中选，值为j的方案数；则dp[i][j] = dp[i - 1][j] + dp[i - 1][j ^a[i]]; 代码： #include<stdio.h>#include<string.h>#include<algorithm>