jump专题
【HDU】4862 Jump 费用流
传送门:【HDU】4862 Jump 题目大意:给你一个N行M列个格子的矩阵,矩阵每个格子中有一个值(0~9),一开始你有活力值为0,然后你可以进行最多K次游戏,每次可以任选矩阵中的一个点作为顶点,然后开始游戏,每次你可以选择从这个点跳到它的右边的点或者下边的点或者不动。每次跳跃,你将支付两个点的曼哈顿距离-1的活力值,能量值可以为负。如果一次跳跃的起点和终点的格子中的值相同,你的活
LeetCode 45 Jump Game II
题意: 给出一个步长数组nums,如果一个人站在i这个点上那么他可以向右最多走nums[i]步,求从左端点走到右端点的最少步数。 思路: 如果点x可以用dp[x]步到达,那么[ x + 1, x + nums[x] ]区间内的点都可以用dp[x] + 1步到达。 利用这个想法,可以O(n)的求出走一步可以到达哪些位置,走两步可以到达哪些位置,以此类推。 代码: clas
1001 Jump and Jump...
1001 Jump and Jump...首先算出每个人的成绩,然后sort一下就好了,考虑n的范围只有2或者3,只要用if+swap也是可行的。/************************************************ Author: fisty* Created Time: 2015/1/24 19:02:10* File Name : BC_1.cpp*****
Leetcode 045 Jump Game II(DP)
题目连接:Leetcode 045 Jump Game II 解题思路:动态规划,dp[i]表示到第i个位置最少需要几步。用一个优先队列维护在第i个位置之前最小的dp[k]值,每次取出一个最小的k,判断k+num[k]是否大于等于i,如果大于等于,那么dp[i] = dp[k] + 1;否则删除k,并再取出优先队列的头,直到dp[i]被更新,然后将dp[i]也放入优先队列中。 class So
*LeetCode 55. Jump Game
https://leetcode.com/problems/jump-game/ 做完Jump Game ii 才做的这个,所以直接就考虑O(n)做法 #include <cstdio>#include <cstring>#include <algorithm>#include <iostream>#include <vector>using namespace std;cl
**LeetCode 45. Jump Game II 思维题
https://leetcode.com/problems/jump-game-ii/ 这道题很不错,我的一种代码感觉本质上跟Ans一样,但是TLE....因为我的写法还是会有重复 思路一:DP 倒过来看,dp[lastIdx-1]=0, dp[i] = min(1+dp[i+k]) k=1,2....nums[i]. 果断TLE const int MAX = 1
leetcode55-Jump Game
题目 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 示例 1: 输入:nums = [2,3,1,1,4] 输出:true 解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。 分析 数组
LeetCode--55. Jump Game
题目链接:https://leetcode.com/problems/jump-game/ 这是个十分有趣的题目。从起点(数组索引0)出发,移动k(k<=nums[0])个位置到达下一个位置(数组索引为i),继续移动k(k<=nums[i])个位置,就这样看是否有一条走法能到达终点(数组索引nums.length-1)。当走到某个位置i时nums[i]==0时就意味着这个走法行不通了!可以看到理
LeetCode - jump-game
题目: Given an array of non-negative integers, you are initially positioned at the first index of the array. Each element in the array represents your maximum jump length at that position. Determine
PHP 跳转搜索(Jump Search)
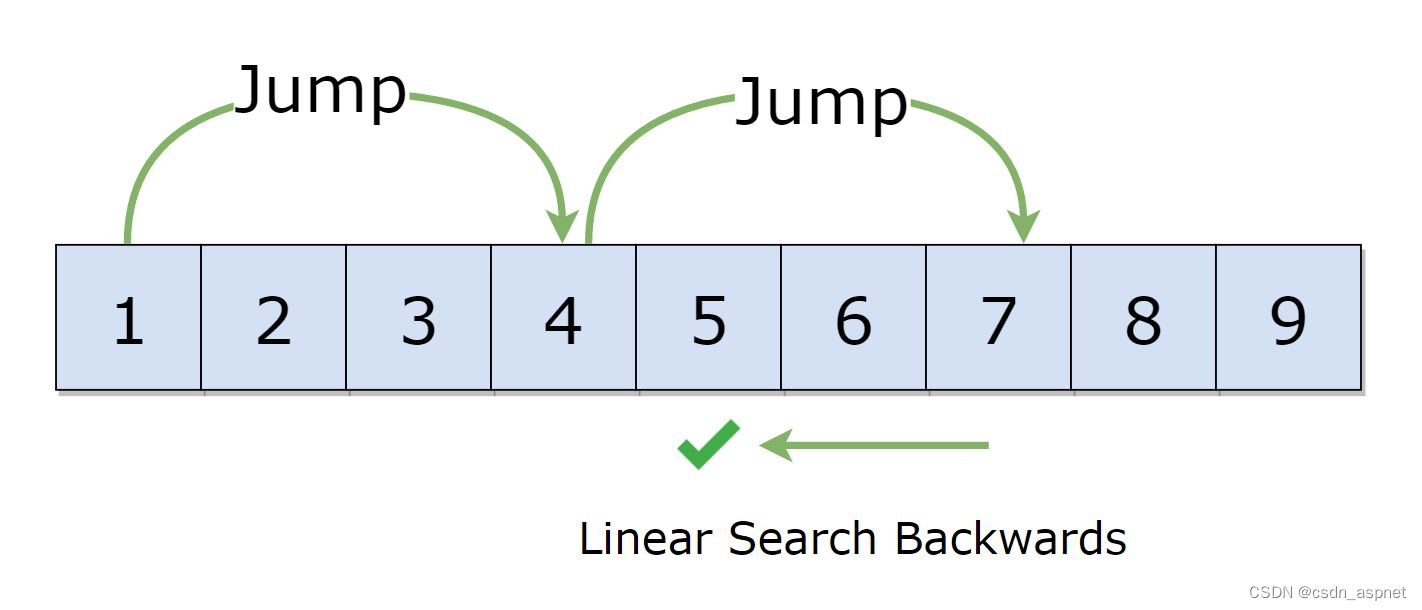
与二分搜索一样,跳转搜索是一种针对排序数组的搜索算法。基本思想是通过按固定步骤向前跳跃或跳过某些元素来代替搜索所有元素来检查更少的元素(比线性搜索)。例如,假设我们有一个大小为 n 的数组 arr[] 和一个大小为 m 的块(要跳转)。然后我们在索引 arr[0]、arr[m]、arr[2m]…..arr[km] 等中搜索。一旦找到区间 (arr[km] < x < arr[(k+
let 55 Jump Game
主题思想: 这个和Jump GameII 是类似的题 做题思路就是贪心算法, 首先获取最大可以走到的下标,然后依次走一步,记录在走到上一次计算到的最大下标位置时出现的最大值,当走到上一次计算的最大下标时,更新下一步可以到达的最大下标,如果下一步可以到达的下标大于数组最后一个元素下标,则可以到达。如果等于当前下标,说明止步不前,则无法到达数组最后一个元素。 AC代码: class Soluti
let 45 Jump Game II
主题思想: 这是一道贪心算法, 要尽可能地跳的远,首先 明确什么时候更新步数, 根据当前i 能知道从i 能走到的最大步数 ith-long,在没走到ith-long达到的最大步数之前,记录中间步骤所能更新的最大值,当i达到ith-long 是更新下一步最大值为中间的最大值,并更新步数。 class Solution {public int jump(int[] nums) {if(nums==n
error: jump to case label error: crosses initialization of xxx
今天写ojb-c的代码,遇到了这样一个问题,error: jump to case label error: crosses initialization of xxx 交叉初始化~! 问题出在case语句内定义的变量的作用域上面。 因为 本地变量的作用域仅在花括号之间。 只要把每个case语句用括号(" {} ")括起来, 变量的作用域限定在相应case语句之内, 就不会出现交叉
最快速的寻路算法 Jump Point Search
作者:runzhiwang,腾讯 TEG 后台开发工程师 本文介绍一种跳点搜索算法 JPS 以及其四个优化算法,其寻路速度最快可是 A*算法的 273 倍。文中的 JPS-Bit 和 JPS-BitPrune 都支持动态阻挡。 1.引言 寻路算法用途众多,例如在游戏和地图中。A*算法已经众所周知,对于其优化也是层出不穷,然而性能并没有取得突破性进展。本文介绍 JPS 的效率、多线程、内存、
This view is not constrained. It only has designtime positions, so it will jump to (0,0) at runtime
问题: This view is not constrained. It only has designtime positions, so it will jump to (0,0) at runtime 此问题虽然不影响编译,但实际控件位置不会跟设计时一样 解决方案: 选中“按钮1”,添加约束
[CodeChef Jump]Jump mission
Jump mission 题解 简单树套树。 首先看到这道题,我们很容易想到 d p dp dp。 设 d p i dp_{i} dpi表示选择跳到了第 i i i座山时总的消耗能量的最小值,容易得到 d p dp dp转移式, d p i = min j < i ∧ p j < p i ( d p j + ( h i − h j ) 2 + a i ) = min j < i
WX:jump_table
第一次接触dialog 看SDK代码注意到一个有意思的数组 jump_table_base并且第二个成员是main函数现在仅凭个人经验分析一下注意它是一个数组哦!const uint32_t* const jump_table_base[92] __attribute__((section("jump_table_mem_area"))) ={(const uint32_t*) TASK
零经验也能表演特技!JUMP想要重新定义虚拟现实
全文共2066字,预计学习时长6分钟 图源:unsplash “如果你可以表演一项世界上最危险、技术最为复杂的特技,且不用接受任何培训,不用具备跳伞经验,也不用花钱购买并安装设备,还不用冒着死亡的风险就可以圆满完成任务,你会为此付出什么呢?”——JUMP公司 笔者采访了JUMP公司的首席执行官詹姆斯·詹森(JamesJensen)。JUMP公司是一家虚拟现实(VR)公司,旨在让用户在
leetcode-55 Jump Game
原题链接: http://oj.leetcode.com/problems/jump-game/ 这道题是动态规划的题目,所用到的方法跟是在Maximum Subarray中介绍的套路,用“局部最优和全局最优解法”。我们维护一个到目前为止能跳到的最远距离,以及从当前一步出发能跳到的最远距离。局部最优local=A[i]+i,而全局最优则是global=Math.max(global, loc
55. Jump Game(Leetcode每日一题-2020.04.17)
占坑 Ref https://leetcode-cn.com/problems/jump-game/solution/55-by-ikaruga/
【LeetCode 面试经典150题】55. Jump Game 跳跃游戏
55. Jump Game 题目大意 You are given an integer array nums. You are initially positioned at the array’s first index, and each element in the array represents your maximum jump length at that position.
[leetcode刷题系列]Jump Game II
利用stack优化, 然后每次dp的时候二分查找就好了nlgn的解法,想&写出来只需要6 const int MAXN = 1e6 + 10;int stk_top = 0;int dp[MAXN], stk[MAXN];class Solution {public:int jump(int A[], int n) {// Start typing your C/C++ solution
[leetcode刷题系列]Jump Game
也许算是dp把- - class Solution {public:bool canJump(int A[], int n) {// Start typing your C/C++ solution below// DO NOT write int main() functionint last = n - 1;for(int i = n - 2; i >= 0; -- i){i
json_load_jump
# coding=utf-8 import json #json.load with open("douban.json","r",encoding="utf-8") as f: #f就是一个类文件对象 t = json.load(f) print(type(t)) #json.dump with open("douban1.json",
JAVA算法:Jump Game 45题和55题算法详解
在LeetCode中45题和55题是关于Jump Game的问题,下面来看看这两道题目的求解方法。 这两个题目的区别是:55题的要求判断你是否能够从开始位置跳到结束位置;而45题的要求是求你从开始位置能够跳到结束位置的最小跳跃次数。。 原题链接: 55. Jump Game https://leetcode.com/problems/jump-game/ Given an array of
LeetCode刷题:55. Jump Game 跳跃游戏
LeetCode刷题:55. Jump Game 跳跃游戏 原题链接:https://leetcode.com/problems/jump-game/ Given an array of non-negative integers, you are initially positioned at the first index of the array. Each element in th