参考Homogeneous Coordinates ，Michigan Technological University 的 Dr. C.-K. Shene写的Introduction to Computing with Geometry Tutorial之中的一部分，摘录+翻译。 引入齐次坐标系的原因之一是为了描述infinity（无穷远点）。 One of the many purpos

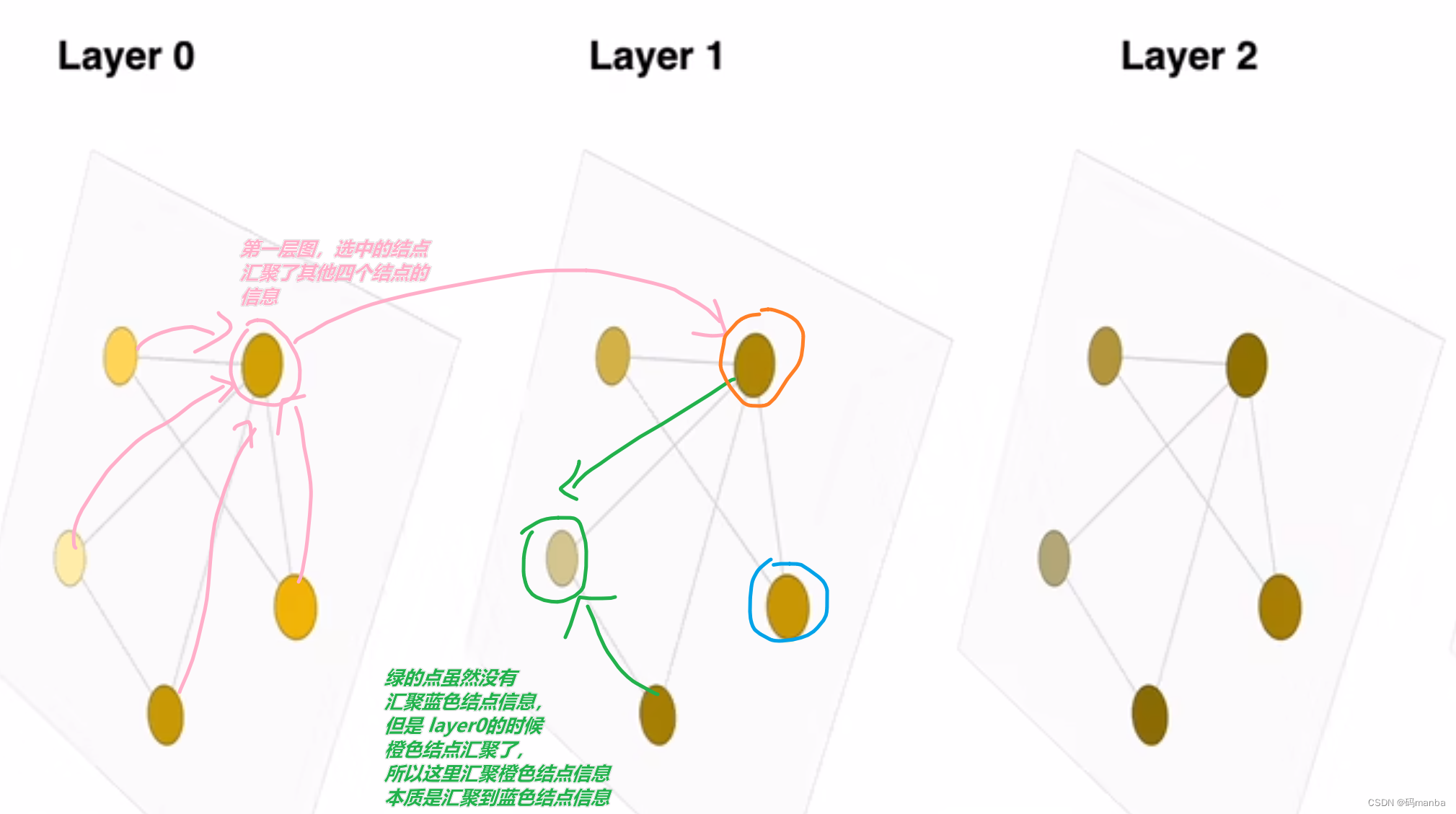
Homogeneous Graph与Heterogeneous Graph 提供图训练的小知识Homogeneous Graph与Heterogeneous Graph的区别在DGL(Deep Graph Library) 定义 同构图在DGL(Deep Graph Library) 定义 异构图 提供图训练的小知识 在一张图进行训练时， 可能由于层数的增加，使得结点可以充分

目录 距离的测验 齐次坐标（Homogeneous Coordinate） 透视投影（Perspective Projection） 投影实战 学前概念 透视投影法(perspective projection method)一种投影法。所谓透视，即穿过透明体观察物体。在人与物体之间，设立一个透明的平面，称作画面(即投影面)，人眼的位置称视点(即投影中心COP)，由视点至物体上各个

转载：http://www.360doc.com/content/11/0410/18/3698714_108650801.shtml（非源出处）  齐次坐标表示是计算机图形学的重要手段之一，它既能够用来明确区分向量和点，同时也更易用于进行仿射（线性）几何变换。”—— F.S. Hill, JR。 对于一个向量v以及基oabc，可以找到一组坐标(v1,v2,v3)，使得v = v1 a +