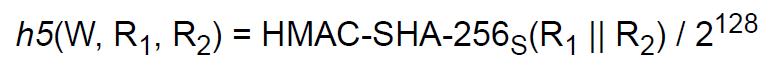e2专题

DALL·E2最详细解读篇章

CLIP被证明其可以学习到鲁棒的图像特征，可以有效的捕获图像的语义和风格，且具有很强的zero-shot能力。另外，Diffusion是目前最优的生成式框架，其推动了图像、视频生成任务的最先进性能。Classifier-Free Diffusion指导技术以样本多样性为代价提高了样本保真度，达到了最佳结果。本文通过结合这两种方法设计了一个图像生成模型DALL-E2，以充分利用CLIP的特征。

DALL-E2详解

标题： DALL-E2详解摘要：本文将详细介绍DALL-E2，OpenAI最新推出的人工智能图像生成模型。DALL-E2在图像生成领域取得了显著进展，它不仅能够生成逼真的图像，还能根据文本描述创造出新颖且具有创意的视觉内容。本文将探讨DALL-E2的技术原理、模型架构、训练过程以及其在艺术创作、设计和娱乐等领域的应用前景。关键词： DALL-E2, 人工智能, 深度学习, 图像生成, O

E2. Close Tuples (hard version)（组合数）

链接 https://codeforces.com/contest/1462/problem/E2 This is the hard version of this problem. The only difference between the easy and hard versions is the constraints on k and m. In this version of th

蓝牙Classic加密算法设计和实现，SAFER+，E0，E1，E2，E3(python)

概述之前用python给大家实现了所有LE相关加密工具算法。bobwenstudy/BluetoothCryptographicToolbox: LE SMP加密算法设计和实现(python) (github.com)，最近重温了下Classic加密，顺便将Classic所有加密算法给实现了一遍。在蓝牙Classic Spec中，有一个很重要的概念就是加密，Secure Connectio

html标记的典型应用e2_7示例

html标记的典型应用e2_7示例 <html><head><title>标记的典型应用</title></head><body><form action="" method="post" name="myform"><table width="694" border="0" align="center" cellpadding="0" cellspacing="0"

Educational Codeforces Round 75 (Rated for Div. 2)E2. Voting (Hard Version)

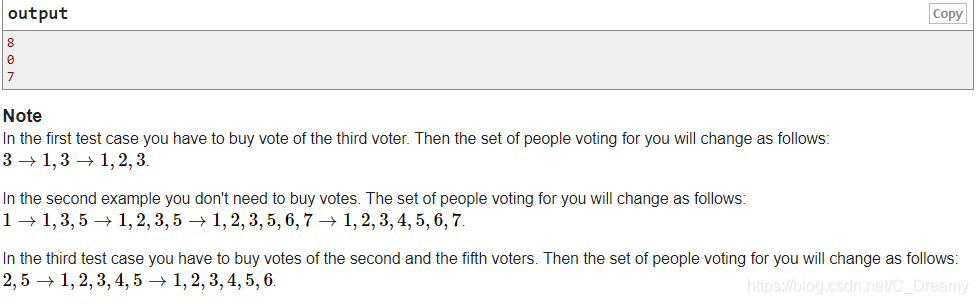
题目链接：https://codeforces.com/contest/1251/problem/E2 题目大意：有n个人要投票，每个人有两个属性m和p，表示当有m个人投票时，他就会免费投票，否则就需要花p元让他投票，问最少花多少钱能让n个人都投票题目思路：E题，过的人这么少，代码竟然如此简单并没有算法，让我挺惊讶的，以后还是不能被人数吓到。这题贪心非常巧妙。如何才能让花的钱

Codeforces 1632 E2. Distance Tree (hard version) —— 思维，有丶东西

This way 题意：给你一棵树，每条边权为1，f(x)表示点x到1的路径上权重和。你可以增加一条边权为k的边，使得f(x)最大值最小。问你k在[1,n]时最大f(x)最小是多少。题解：我想着只搜一次，搜的时候维护上面距离当前点最远的点的距离。我感觉可以是树链剖分或者动态开点线段树，然后加一些骚操作，但是好累啊，想想都绝望，写写200行打底。于是放弃了，还是看题解去。毕竟有段

Codeforces Round#769(Div.2)E1+E2 Distance Tree

题目树是无环的连通无向图。加权树具有分配给每条边的权重。两个顶点之间的距离是连接它们的路径上的最小权重之和。给定一棵具有 n 个顶点的加权树，每条边的权重为 1。将 d(v) 表示为顶点 1 和顶点 v 之间的距离。如果可以在任意两个顶点 a 和 b (1≤a,b≤n) 之间临时添加一条权重为 x 的边，则令 f(x) 为 max{d(v),1<=v<=n} 的最小可能值。请注意，经过此操

E2. 比昨天更多的棒棒糖 (Hard)

http://www.cnblogs.com/hua-dong/p/8011232.html

【论文精读】DALL·E2

摘要 CLIP被证明其可以学习到鲁棒的图像特征，可以有效的捕获图像的语义和风格，且具有很强的zero-shot能力。另外，Diffusion是目前最优的生成式框架，其推动了图像、视频生成任务的最先进性能。Classifier-Free Diffusion指导技术以样本多样性为代价提高了样本保真度，达到了最佳结果。本文通过结合这两种方法设计了一个图像生成模型DALL-E2，以充分利用

瑞萨RL78G12系列单片机使用IAR软件进行仿真设置及与E2接线

目录一、单片机与仿真器连接二、IAR软件在线仿真使用手册一、单片机与仿真器连接 E1引脚接线图 RL78系列单片机的GND接仿真器的pin2、pin12、pin14 RL78系列单片机的VDD接仿真器的pin8 RL78系列单片机的Tool0接仿真器的pin5 RL78系列单片机的Reset接仿真器的pin10、pin13 二、IAR软件在线仿真使用手册

【扩散模型】9、DALL-E2 | 借助 CLIP 的图文对齐能力来实现文本到图像的生成

文章目录一、背景二、方法2.1 Decoder2.2 Prior 三、图像控制3.1 Variations3.2 Interpolations3.3 Text Diffs 四、探索 CLIP 的潜在空间五、文本到图像的生成5.1 先验的重要性5.2 人类评价5.3 多样性和保真性的平衡5.3 在 COCO 上对比论文：DALLE.2 代码：https://github.

E2. Voting (Hard Version)（思维）

有 n 个人，每个人有 mi 和 pi ，mi 代表着如果有 mi 个人投票给他，那么他就免费投票给他，否则你需要花费pi的代价来收买他。请问最少花费多少使得所有人都投他。看到 m 数组的数据范围，m 数组作为数组下标应该是没得跑了，有贪心策略我们应该选择 pi 尽量少的那些人，但是同时要照顾到 m 数组。因为要贿赂的总人数我们不知道，但借用优先队列（小根堆），将目前为止

Codeforces Round 906 (Div. 2)（D推公式 E1分类讨论区间 E2 dp+线段树）

A - Doremy's Paint 3 推公式得 b1=b3=b5=b7.... b2=b4=b6=b8... 所以如果只有一个数或者两个数且数量差小于等于1即可 #include<bits/stdc++.h>using namespace std;const int N = 2e5+10,mod=1000003;#define int long longtypedef lon

设栈S和队列Q的初始状态为空，元素e1、e2、e3、e4、e5、e6依次通过栈S，一个元素出栈后即进入队列Q，若6个元素出队的序列是e2、e4、e3、e6、e5、e1，则栈S的容量至少应该是

题目设栈S和队列Q的初始状态为空，元素e1、e2、e3、e4、e5、e6依次通过栈S，一个元素出栈后即进入队列Q，若6个元素出队的序列是e2、e4、e3、e6、e5、e1，则栈S的容量至少应该是 3 解答出队先出e2表示e1，e2进栈后出e2(这时栈的容量最大为2)，接着出e4，e3表示e3，e4进栈后出e4，e3(这时栈的容量最大为3)，再出e6，e5表示e5，e6进栈后出e6，e5(

最新Ai系统ChatGPT程序源码+以图生图+Dall-E2绘画+支持GPT4+Midjourney绘画

使用GHS和Renesas E2调试RH850 1372

文章目录前言工程配置工程调试总结前言 RH850系列和其他芯片一样，除了Lauterbach,Isystem之外，也有便宜的刷写/调试器，如E2,E1。本文介绍利用E2调试器，联合GreenHills编译器对1372芯片调试工程配置在开始调试之前，需要确保工程能够正常编译生成elf. 打开工程，配置connect 点击Connection Organizer配置