curves专题
uva 1476 - Error Curves(三分)
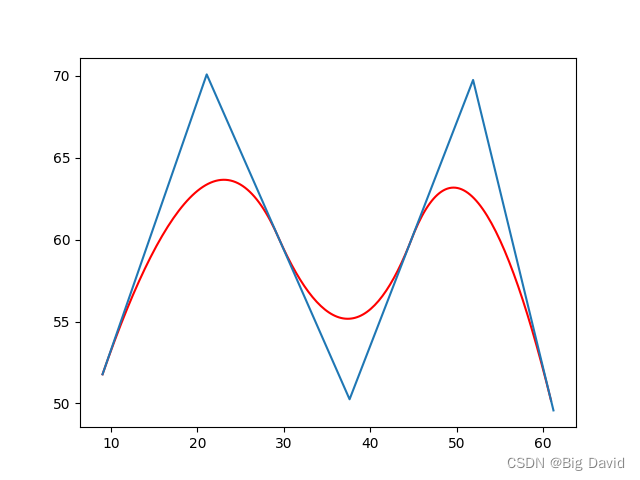
题目链接:1476 - Error Curves 题目大意:给定n条二次曲线S(x),定义F(x)=max(Si(x)), 求出F(x)在0~1000上的最小值。 解题思路:数值方法,三分。 #include <cstdio>#include <cstring>#include <algorithm>using namespace std;const int maxn = 100
Analyzing Receiver Operating Characteristic Curves With SAS
版权声明:原创作品,允许转载,转载时请务必以超链接形式标明文章原始出版、作者信息和本声明。否则将追究法律责任。 http://blog.csdn.net/topmvp - topmvp As a diagnostic decision-making tool, receiver operating characteristic (ROC) curves provide a comprehe
局部路径规划算法 - B样条曲线(B-spline Curves)
参考资料: (1)B样条曲线(B-spline Curves) (2)B样条曲线法 1 算法概述 1.1 算法简介 样条是一根富有弹性的细木条或塑料条,在应用CAD/CAM技术以前,航空、船舶和汽车制造业普遍采用手工绘制自由曲线。绘制员用压铁压住样条,使其通过所有给定的型值点,再适当地调整压铁,改变样条形态,直到符合设计要求。B样条曲线是B-样条基函数(给定区间上的所有样条函数组成一个线性空
Zbrush中怎么通过Curves Tubes创建手指
之前我们已经能够初步完成了模型的人体躯干,今天的Zbrush教程将继续使用Curves Tubes创建手指,实现更细致的塑形。文章内容仅以fisker老师讲述为例,您也可以按照自己的想法,跟着老师的步调进行创作,让模型更富有创造力。 调整模型比例:将Draw绘制模式切换为Scale缩放模式,对模型七头身比例和体型进行进一步调整,按住Shift键可以让模型等比例放大或缩小。
如何通过ZBrush中的Curves和Insert笔刷创建四肢
之前的ZBrush教程给大家介绍了人体结构比例和肌肉走向,同时使用ZBrush®软件中的CuverTube笔刷为模型添加了颈部和手臂、使用InsertSphere笔刷添加腰部,本讲将继续使用Curves和Insert笔刷创建四肢,实现人体结构框架。这部分主要是腿部的创建以及肌肉的塑造,以体现干瘦的僵尸形体和皮肤破裂的视觉效果。 创建模型腿部:依然CurveTube笔刷拖拽出大腿效果,
Error Curves HDU - 3714(三分)
Error Curves 题目链接:HDU - 3714 题意:x在区间[0,1000]取值时,n个函数中的最大值的最小值;(最大值指x固定,n个函数的最值; 最小值指在所有得到的最大值中的最小值); 三分x; 注意精度问题!!!此题精度要高!!! #include <bits/stdc++.h>#define eps 1e-10//就是这里一开始是1e-8一直WA,,
NX二次开发UF_CURVE_ask_int_curves 函数介绍
文章作者:里海 来源网站:https://blog.csdn.net/WangPaiFeiXingYuan UF_CURVE_ask_int_curves Defined in: uf_curve.h int UF_CURVE_ask_int_curves(tag_t int_curve_object, int * num_curves, tag_t * * intersection_curv
Uva - 1476 - Error Curves(三分)
题意:求函数F(x) = max(S(x)) 的最小值。S(x) = a*x^2 + b*x + c(0 ≤ a ≤ 100),输入多个S(x)。 题目链接:http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&category=493&problem=4222 ——>>做的
BLS embedded curves族
1. 引言 以太坊基金会Antonio Sanso 2023年论文 Family of embedded curves for BLS中,展示了源自BLS椭圆曲线的embedded curves。 pairing-friendly curve E E E具有bilinear map e : G 1 × G 2 → G T e:\mathbb{G}_1\times \mathbb{G}_2\
具有形状参数的新型广义混合三角贝齐尔样曲线(GHT_Bezier_curves) matlab实现
具有形状参数的新型广义混合三角贝齐尔样曲线 一、n维 GHT-Bernstein 基函数1、定义2、性质: 二、基函数的matlab程序实现1、程序:2.2 基函数图像 三、n维GHT-Bézier曲线(GHT-Bézier Curves of Degree n)相应程序:相应结果:注:得到的曲线应该满足凸包性质,但是有几个参数得到的曲线不在控制多边形里面(如b图中红色曲线),程序检查了几遍
B-spline Curves 学习之B样条基函数计算实例(3)
B-spline Basis Functions: Computation Examples 1. 简单节点(Simple Knots ) 假设节点向量是U = { 0, 0.25, 0.5, 0.75, 1 }. 因此, m = 4 和u0 = 0, u1 = 0.25, u2 = 0.5, u3 = 0.75 及 u4 = 1。0次(degree)基函数很简单
κ-Curves: Interpolation at Local Maximum Curvature
Abstract Introduction Related Work Smoothness Optimization Result Conclusion
κ-Curves: Interpolation at Local Maximum Curvature
Abstract Introduction Related Work Smoothness Optimization Result Conclusion