B-spline Curves 学习之B样条基函数计算实例（3）

本文主要是介绍B-spline Curves 学习之B样条基函数计算实例（3），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

B-spline Basis Functions: Computation Examples

1. 简单节点（Simple Knots ）

　　假设节点向量是U = { 0, 0.25, 0.5, 0.75, 1 }. 因此, m = 4 和u0 = 0, u1 = 0.25, u2 = 0.5, u3 = 0.75 及 u4 = 1。0次（degree）基函数很简单。它们分别是定义在节点跨度 [0,0.25,), [0.25,0.5), [0.5,0.75) 和 [0.75,1)上的N0,0(u), N1,0(u), N2,0(u)和N3,0(u) ,如下图所示。

下表给出了所有的Ni,1(u)：

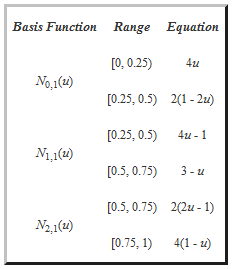
　　接着展示这些基函数的图形。因为内节点0.25, 0.5和0.75都是简单的(即， k = 1) 且p = 1，有p - k + 1 = 1非零基函数和三个节点。而且， N0,1(u), N1,1(u) 和 N2,1(u)在节点0.25, 0.5 和 0.75分别是C0 连续的。

　　从Ni,1(u)可计算2次基函数。因此m = 4, p = 2, 和 m = n + p + 1，我们有n = 1所以只有两个2次基函数：N0,2(u)和 N1,2(u). 结果见下表：

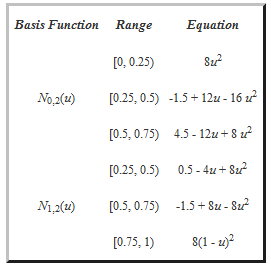
　　下图显示了两个基函数。三条垂直蓝线表示节点位置。注意每个基函数是三个2次曲线段的组合曲线。例如，N0,2(u) 是绿色曲线，其是定义在[0,0.25), [0.25, 0.5) 和 [0.5,0.75)上的三个抛物线的联合。这些曲线段连接在一起形成一个光滑的钟形。请验证 N0,2(u,) (resp., N1,2(u)) 在节点 0.25 和 0.5 (resp., 0.5 和 0.75)是C1 连续的。如前页所提到的，在节点处，这个复合曲线是C1 连续的。

2. 带正重复度的节点

　　如果一个节点向量包含有正重复度的节点，我们会遇到 0/0的情况，后面会遇到。因此我们定义 0/0 等于0。幸运的是，这只用于手工计算的情况。对计算机实现，有个有效的算法，不受这个问题影响。如果ui 是重复度 k 的节点(即ui = ui+1 = ... = ui+k-1), 那么节点区间[ui,ui+1), [ui+1,ui+2), ..., [ui+k-2,ui+k-1) 不存在，结果是，Ni,0(u), Ni+1,0(u), ..., Ni+k-1,0(u) 都是零函数。

　　考虑节点向量 U = { 0, 0, 0, 0.3, 0.5, 0.5, 0.6, 1, 1, 1 }. 因此，0 和1 是重复度3 (即， 0(3)和 1(3)) 而 0.5 是重复度2 (即， 0.5(2)). 结果是， m = 9而节点分配是

　　现在计算 Ni,0(u)。注意因为 m = 9 且 p = 0 ( 0 次基函数), 我们有n = m - p - 1 = 8。如下表所示，只有四个0次非零基函数： N2,0(u), N3,0(u), N5,0(u) 和 N6,0(u).

然后，我们继续计算1次基函数。因为 p 为 1, n = m - p - 1 = 7. 下表显示了结果：

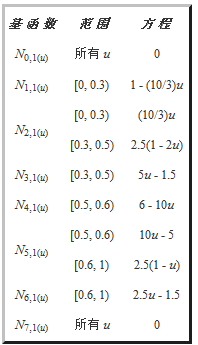
　　下图显示了这些基函数的图形。

　　让我们看一个特别的计算，比如N1,1(u). 。它使用下式计算的：

　　将u1 = u2 = 0 和 u3 = 0.3 代入这个方程产生下式：

　　因为 N1,0(u) 到处为零，第一项是0/0 因此被定义为零。因而，只有第二项对结果有影响。因为 N2,0(u) 在[0,0.3)上是1， N1,1(u) 在 [0,0.3)上是1 - (10/3)u 。

　　接着，让我们计算所有的Ni,2(u)。因为 p = 2, 我们有 n = m - p - 1 = 6。下表包含了所有的Ni,2(u):

　　下图显示了所有2次基函数。

　　让我们选一个典型的计算作为例子，如N3,2(u)。计算式是下式：

　　代入 u3 = 0.3, u4 = u5 = 0.5 和 u6 = 0.6得到

　　因为 N3,1(u) 在 [0.3, 0.5)上非零且等于5u - 1.5，(5u - 1.5)2 是N3,2(u) 在[0.3, 0.5)上的非零部分。因为N4,1(u) 在 [0.5, 0.6)上非零且等于6 - 10u, (6 - 10u)2 是 N3,2(u) 在[0.5, 0.6)上的非零部分。