clarke专题
【HDU】5566 Clarke and room【树链剖分+AC自动机】
题目链接:Clarke and room #include <bits/stdc++.h>using namespace std ;typedef long long LL ;#define ls ( o << 1 )#define lson ls , l , m#define rs ( o << 1 | 1 )#define rson rs , m + 1 , r#define rt
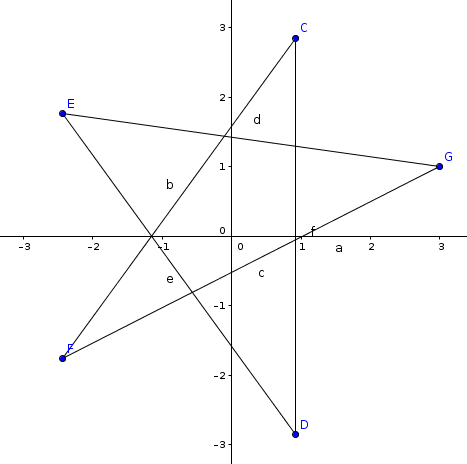
BestCoder Round #62 (div.2)Clarke and five-pointed star(极角排序,判断五边形)
题目链接 题意:给你五个点,问这五个点是否可以组成正五边形(正五角星,等价于正五边形)。 解答:先极角排序,(让五个点按照顺时针或者逆时针的顺序)然后我们计算五条边是不是一样,然后在看对角线是不是都一样。 #include<cstdio>#include<iostream>#include<algorithm>#include<cmath>#include<set>#includ
BestCoder Round #62 (div.2)Clarke and food (简单贪心)
题目链接 题意:有个背包容量是V,现在有n个物品,每个物品有一个体积,问背包最多能装多少个。 解法:先排序,从小到大选。 #include<cstdio>#include<iostream>#include<algorithm>#include<cmath>#include<set>#include<map>#include<string>#include<cstring>
狄利克雷卷积 【HDU5628】Clarke and math
题目大意: 给定f(1~n),求g(1~n) 题目分析:(狄利克雷卷积) 狄利克雷卷积: 狄利克雷卷积满足:交换律,结合律,分配率等性质(和乘法是一样的)。 我们设函数g(i)=1 如果k==1,则 i 的答案为: (f∗g)(n)=∑d1|nf(d1) ( f ∗ g ) ( n ) = ∑ d 1 | n f ( d 1 ) (f*g)(n)=\sum_{d_1|n}{f
Clarke Valve完成550万美元风投融资轮,由OGCI Climate Investments领投
罗德岛北金斯顿--(美国商业资讯)--Clarke Valve今日完成了550万美元B轮优先股的发售,销售对象为由OGCI Climate Investments领投的一组投资者。加上Aramco Energy Ventures和Chevron Technology Ventures的注资,Clarke如今已通过B轮融资筹集了1,550万美元的资金。 Clarke专利百叶阀的重量、大小和成
Clarke and MST HDU - 5627
http://acm.hdu.edu.cn/showproblem.php?pid=5627 要求一棵且运算结果最大的SPT 肯定不能简单按权值排序 贪心考虑 枚举二进制位 如果2^i可以被满足 完全可以牺牲掉2^(i-1) 2^(i-2)... 枚举到2^i时 从目前所有边中找出边权的二进制位中i位为1的边 看能否将图连通 能的话就把低位的范围限定在所有边权的二进制位中i位为1的边中 若不
Clarke and MST(最大生成树)
克拉克是一名人格分裂患者。某一天克拉克变成了一名图论研究者。 他学习了最小生成树的几个算法,于是突发奇想,想做一个位运算and的最大生成树。 一棵生成树是由n-1n−1条边组成的,且nn个点两两可达。一棵生成树的大小等于所有在生成树上的边的权值经过位运算and后得到的数。 现在他想找出最大的生成树。输入描述第一行是一个整数T(1 \le T \le 5)T(1≤T≤5),表示数
hdu5628 : Clarke and math(线性筛)
这题以前用快速幂写的 今天用线性筛写了一下,真刺激 大概就是说那个东西是 f∗1k f ∗ 1 k f*1^k 然后你只要算出来 1k 1 k 1^k 就可以 O(nlogn) O ( n l o g n ) O(nlogn)卷积了 关于算 1k 1 k 1^k当然可以直接快速幂 O(nlognlogk+nlogn) O ( n l o g n l o g k + n
【HDU5565 BestCoder Round 62 (div1)C】【STL or 二分答案 or 计数排序】Clarke and baton n个人减肥m次求最后异或值
【HDU5565 BestCoder Round 62 (div1)C】【优先队列做法】Clarke and baton n个人减肥m次求最后异或值 #include<stdio.h> #include<string.h>#include<ctype.h>#include<math.h>#include<iostream>#include<string>#include<se
HDU 5562 Clarke and five-pointed star (BC)
Clarke and five-pointed star Time Limit : 2000/1000ms (Java/Other) Memory Limit : 65536/65536K (Java/Other) Total Submission(s) : 8 Accepted Submission(s) : 2 Font: Times New Roman | Verd