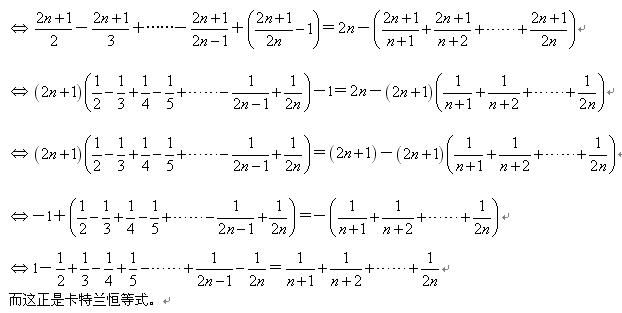Catalan数的定义令h(1)=1，Catalan数满足递归式：h(n) = h(1)*h(n-1) +h(2)*h(n-2) + ... + h(n-1)h(1)，n>=2该递推关系的解为： 证明： 令1表示进栈，0表示出栈，则可转化为求一个2n位、含n个1、n个0的二进制数，满足从左往右扫描到任意一位时，经过的0数不多于1数（也就是1的个数>=0的个数)。显然含n个1、n个0的2n位二进

介绍 Catalan数是组合数学中一个常在各种计数问题中出现的数列。一般项公式为 Cn的另一个表达形式为 一般来说，我们编程时使用递推关系会更方便计算 或 即：C(n) = C(1)*C(n-1) + C(2)*C(n-2) + … + C(n-1)C(1). 它的前几项为: 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796。可以先通

http://poj.org/problem?id=2084 大意：有2n个数字形成一个圆形，直线段连接一对数字，每一个数字必须连接到另一个数字上。（没有相交的线段） 分析： 现在假设1是要连接的点，它和4相连，为了不破坏规矩——“ 没有相交的线段"，2,3只能在右边的圆形区域进行匹配，4——8也不能越过红线，在三角形中进行连线匹配。设n个点的匹配方案数是h(n

来自：http://blog.csdn.net/dlyme/archive/2008/06/10/2532831.aspx   【Catalan数——卡特兰数】 一.Catalan数的定义令h(1)=1，Catalan数满足递归式：h(n) = h(1)*h(n-1) + h(2)*h(n-2) + ... + h(n-1)h(1)，n>=2该递推关系的解为：h(n) = C(2n-2

《数据结构》课程中有个经典的栈应用的例题：开关盒布线问题。这个题用栈来解决是非常奇妙的，题目是说给定一种布线情况，判断是否出现了短路，短路的定义就是开关盒表面的排线不能出现交叉。思路是顺(逆)时针遍历，遇到起点时入栈，遇到终点时，则将当前栈顶元素出栈，这样到最后若栈空，则布局合法，否则会出现短路。为什么呢？因为任一条线将开关盒表面分成了两个区域，不短路的情况是这两个区域不能出现一个区域包括某条线的

关于扩展的卡特兰数： 1.(n-m+1)/(n+1)*c(n+m,n) 2.c[n+m][n]-c[n+m][m-1] Catalan，Eugene，Charles，卡特兰（1814～1894）比利时数学家，生于布鲁日（Brugge），早年在巴黎综合工科学校就读。1856年任列日（Liege）大学数学教授，并被选为比利时布鲁塞尔科学院院士。 卡特兰一生共发表200多种数学各领域的论著。在微分

http://acm.hdu.edu.cn/showproblem.php?pid=1023 牛人总结：http://yanpol.blog.163.com/blog/static/4817080620106184553824/ #include <stdio.h> int main() { int i,j,yu,temp,n,m,lenth; int s[101][60]; s[1][1