atcoder专题
AtCoder Beginner Contest 370 Solution
A void solve() {int a, b;qr(a, b);if(a + b != 1) cout << "Invalid\n";else Yes(a);} B 模拟 void solve() {qr(n);int x = 1;FOR(i, n) FOR(j, i) qr(a[i][j]);FOR(i, n) x = x >= i ? a[x][i]: a[i][x];pr2(
AtCoder Beginner Contest 369 D - Bonus EXP 动态规划
原题链接: https://atcoder.jp/contests/abc369/tasks/abc369_d 思路: 这道题为什么要用动态规划呢,其实,对于第i个怪物,我们有打与不打两种处理方式,而对于打,我们是获得两倍的经验值,还是一倍的经验值,与我们打了奇数只怪物还是打了偶数只怪物有关了,因此我们定义dp[i][0] 为前i只怪物总共打了偶数次,dp[i][1] 为前i只怪物总
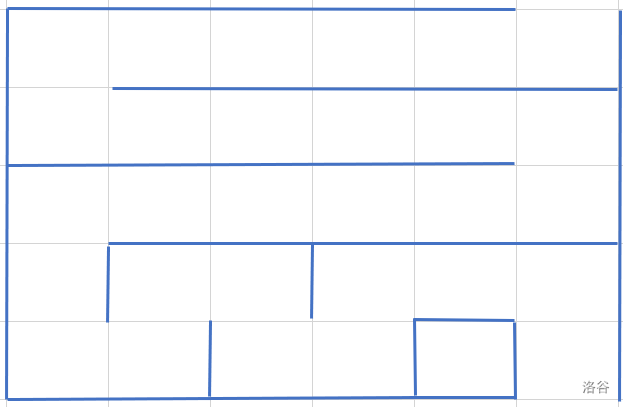
题解AtCoder ABC 358 F Easiest Maze
一道模拟题。 思路 最短的路线是直接竖着走下来,经过 n n n 个格子,所以 k k k 最小是 n n n。如果想要延长路线,可以采用九转大肠的形状,就像这样: 可以发现,每次向左走之后都必须走回来,所以每次新经过的格子数是偶数,得到 k − n k-n k−n 是偶数才有可行的方案。 首先,把整张图表的初始状态设为如下形式(即每个格点都是独立的): +++++S++o|o|o
AtCoder Beginner Contest 369 ABCDE
背景 无 A题:369 思路 假设A<=B 分类讨论,有如下两种情况 1.A==B,情况唯一,另外一个数只能取A 2.A<B,首先我们可以以B-A为公差d构造,另外一个数可以取A-d或者B+d。(然后接着考虑放在A和B中间的情况,样例中给了,只要B-A为偶数即可) 代码 inline void solve() {int a, b; cin >>
AtCoder Beginner Contest 369 A~E
封面原图 画师かにょこ AtCoder Beginner Contest 369 我愿称之为等差数列场 A - 369 题意 给两个数,问能和他们构成等差数列的数有多少个 代码 #include <bits/stdc++.h>#define mod 998244353using namespace std;typedef long long ll;typed
AtCoder Beginner Contest 366(D~E题解)
闲来无事去vp了一下之前放假没打的比赛,感觉需要总结的也就这两题吧,a,c都是水题,b只不过是实现有一点难,并不是很难写,d是一个需要自己推的三维前缀和,e也是一种前缀和,我当时没想到,看了大犇的代码才知道还能这么做 D - Cuboid Sum Query 题意:给你一个三维数组,然后给你q次询问,每次询问有一个起始位置和终止位置,然后问你这个的三维前缀和是什么 思路:用容斥原理推出三
AtCoder Beginner Contest 368 题解思路(A-D,F)
AtCoder Beginner Contest 368 题解&&思路(A-D,F) A - Cut 题目描述 有 N N N 个数在一个桶里面,从上往下第 i i i 个数是 A i A_i Ai,从桶下面取出 K K K 个数,保持原顺序放在桶的上面,从上到下打印写在卡片上的整数。 思路 时间复杂度 O ( N ) . \mathcal{O}(N). O(N). 本质上
Hitachi Vantara Programming Contest 2024(AtCoder Beginner Contest 368)ABCDEF
前言 F比E简单多了,难评 A题:Cut 题意 给定n张卡片,将后m张卡片按顺序放置到顶部,按顺序输出卡片id 思路 更改输出方式即可 代码 inline void solve() {int n, m; cin >> n >> m;vector<int> a(n + 1);for (int i = 1; i <= n; i ++ ) cin >> a[i];for (int i =
D - Pedometer AtCoder Beginner Contest 367
题意: 一个长度为n的数组a首尾相接,求满足a[i]~a[j]的和是m的倍数的[i,j]对数 思路: 由于首位相接,那么区间i-->j的所有数有两种情况:第一种是i<j的情况,第二种是i>j的情况 为了简化处理,我们可以将他变为一个线性数组,也就是原数组的后面再加一个原数组,那么新数组的所有区间就包含了以上两种情况: 设s[i]为前缀和数组,a[i]到a[j]的数的和是m的倍数-
Atcoder - 4142 尺取法,位运算(适合难度:普及+/提高-)
Atcoder - 4142 尺取法,位运算(适合难度:普及+/提高-) 异或不懂的参考位运算 if a ^ b ^ c < a + b + c 说明a ^ b <= a + b \qquad 枚举一个左端点,然后利用双指针计俩来滑动右端点来找到最大的满足条件的右端点。解法和UVA1121是很相似的,都是尺取法。 #include <iostream>#include <
atcoder ABC 359-B题详解
atcoder ABC 359-B题详解 Problem Statement There are 2N people standing in a row, and the person at the i-th position from the left is wearing clothes of color Ai. Here, the clothes have N colors from 1
Atcoder Beginner Contest 359
传送门 A - Count Takahashi 时间限制:2秒 内存限制:1024MB 分数:100分 问题描述 给定 N 个字符串。 第 i 个字符串 () 要么是 Takahashi 要么是 Aoki。 有多少个 i 使得 等于 Takahashi ? 限制 N 是整数。每个字符串 是 Takahashi 或者 Aoki。() 输入格式
AtCoder Beginner Contest 359 A~C(D~F更新中...)
A.Count Takahashi 题意 给出 N N N个字符串,每个字符串为以下两种字符串之一: "Takahashi" "Aoki" 请你统计"Takahashi"出现了多少次。 分析 输入并统计即可。 代码 #include <bits/stdc++.h>using namespace std;typedef long long ll;void solve() {i
atcoder ABC 359-A题详解
atcoder ABC 359-A题详解 Problem Statement You are given N strings. The i-th string Si(1≤i≤N) is either Takahashi or Aoki. How many i are there such that Si is equal to Takahashi? Constraints 1≤N≤10
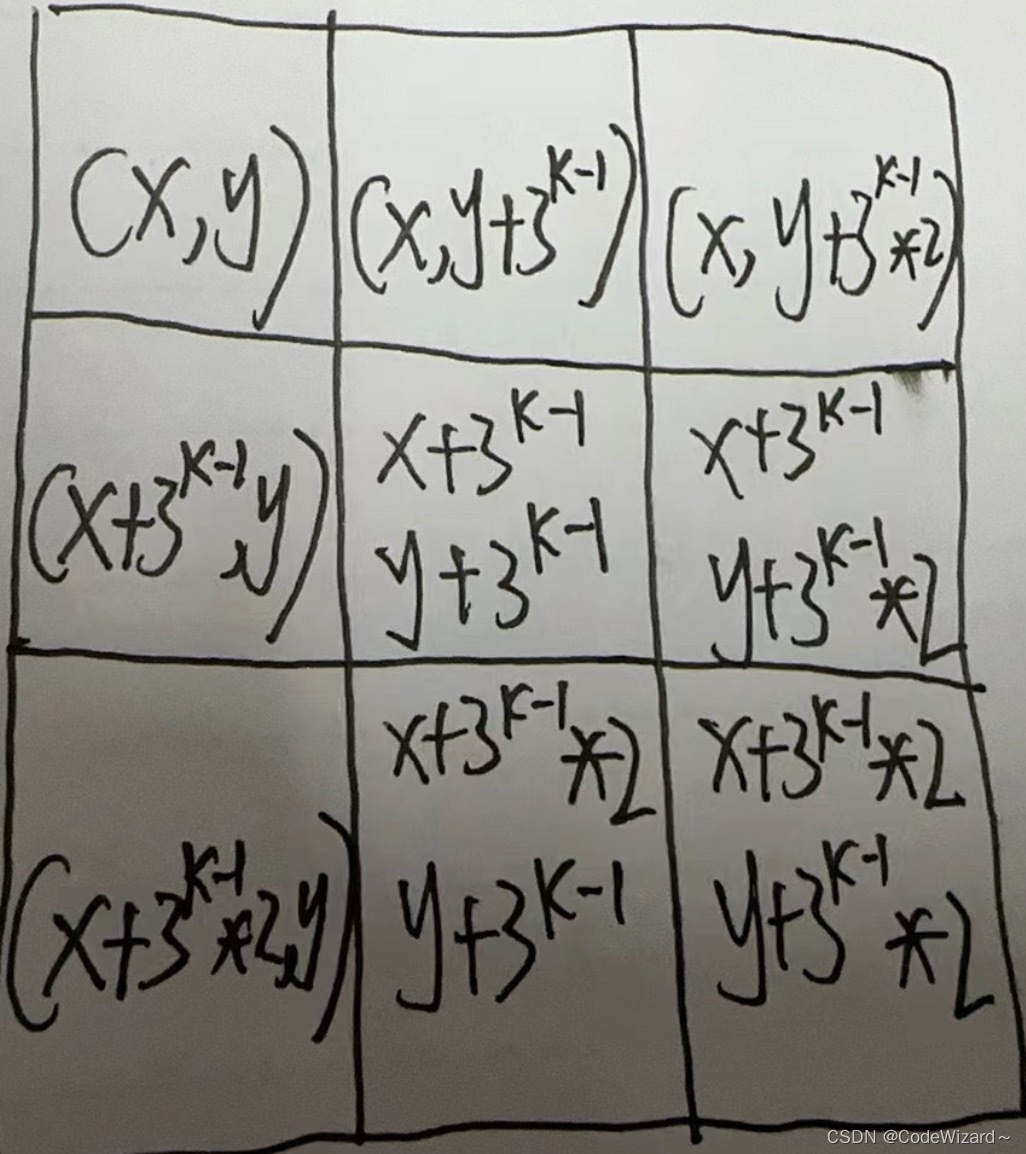
AtCoder ABC 365G 凸包 + 二分
题意 AtCoder ABC 365G Freestyle 题解 考虑任两种操作 ( A i , B i ) (A_{i},B_{i}) (Ai,Bi)和 ( A j , B j ) (A_{j},B_{j}) (Aj,Bj),则他们的任意组合可以表示为 ( t A i + ( 1 − t ) A j , t B i + ( 1 − t ) B j ) \big(tA_{i}+(1-
atcoder ABC 358-B题详解
atcoder ABC 358-B题详解 Problem Statement At the entrance of AtCoder Land, there is a single ticket booth where visitors line up to purchase tickets one by one. The purchasing process takes A seconds p
AtCoder Beginner Contest 358 A~E(F,G更新中...)
A.Welcome to AtCoder Land 题意 给出两个字符串 S , T S, T S,T,请你判断是否满足: 字符串 S S S为AtCoder 字符串 T T T为Land 分析 输入后判断即可 代码 #include<bits/stdc++.h>using namespace std;void solve() {string s, t;cin >> s >
atcoder ABC 357-C题详解
atcoder ABC 357-C题详解 Problem Statement For a non-negative integer K, we define a level-Kcarpet as follows: A level-0 carpet is a 1×1 grid consisting of a single black cell. For K>0, a level-K carp
AtCoder Beginner Contest 355
C - Bingo 2 题意 有一个 n × n n\times n n×n 的网格,初始全白,有 t t t 次操作,每次操作涂黑一个指定的格子。 问执行第几个操作后,有一行或一列或对角线的格子全部被涂黑。 思路 如果暴力判断,那么总时间复杂度是 O ( n 2 t ) O(n^2t) O(n2t) 的,而 n ≤ 2000 , t ≤ 200000 n \le 2000,t \
AtCoder Beginner Contest 357 A~E(F更新中...)
A.Sanitize Hands(模拟) 题意 有 n n n个外星人排队对手消毒,其中第 i i i个外星人有 H i H_i Hi只手需要消毒,已知消毒液共能使用 M M M次,每次可以对一只手消毒,问:总共有多少个外星人的全部手都完成消毒了。 分析 本题并不是一个贪心的题目,而是直接对输入的数据从左往右进行操作,依次判断剩余的消毒液是否足够完成消毒,如果可以,就减去需要使用的量,否
SuntoryProgrammingContest2024(AtCoder Beginner Contest 357)(A~F)(最爱线段树的一集)
A - Sanitize Hands 题意: 模拟 // Problem: A - Sanitize Hands// Contest: AtCoder - SuntoryProgrammingContest2024(AtCoder Beginner Contest 357)// URL: https://atcoder.jp/contests/abc357
AtCoder Regular Contest 179 (ABC题)视频讲解
A - Partition Problem Statement You are given integers N N N and K K K. The cumulative sums of an integer sequence X = ( X 1 , X 2 , … , X N ) X=(X_1,X_2,\dots ,X_N) X=(X1,X2,…,XN) of length
D - Permutation Subsequence(AtCoder Beginner Contest 352)
题目链接: D - Permutation Subsequence (atcoder.jp) 题目大意: 分析: 相对于是记录一下每个数的位置 然后再长度为k的区间进行移动 然后看最大的pos和最小的pos的最小值是多少 有点类似于滑动窗口 用到了java里面的 TreeSet和Map TreeSet存的是数的位置 TreeSet里面有se.last() 获取当前这个里面的最后的这个元素
C - Sigma Problem(AtCoder Beginner Contest 353)
题目的链接: C - Sigma Problem (atcoder.jp) 题目: 样例: 题目大致含意: 给你n个数,让你对这n个数进行操作,比如当前是第i个,那么让a[i] 和 后面的每个数进行相加, 例如a[i] + a[i + 1] 注意的是a[i] + a[i + 1]的结果要进行取模 同理进行操作 (a[i] + a[i + 2]) % mod 输出的结果是 把这些运算
AtCoder Regular Contest 177
A - Excange 题意 用这些零钱能否不找零地买这些物品 思路 因为 500 = 5 × 100 = 10 × 50 = 50 × 10 = 500 × 1 500=5\times 100=10\times 50=50\times 10=500\times 1 500=5×100=10×50=50×10=500×1。 所以说,我们这道题可以采用贪心算法,优先取大的减去目前零钱最大
AtCoder Beginner Contest 353(A~E)
文章目录 A Buildings1.基本思路:2.代码: B - AtCoder Amusement Park1.基本思路:2.代码: C - Sigma Problem1.基本思路:2.代码: D - Another Sigma Problem1.基本思路:2.代码: E - Yet Another Sigma Problem1.基本思路:2.代码: A Buildings