C - Sigma Problem(AtCoder Beginner Contest 353)

本文主要是介绍C - Sigma Problem(AtCoder Beginner Contest 353)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目的链接:

C - Sigma Problem (atcoder.jp)

题目：

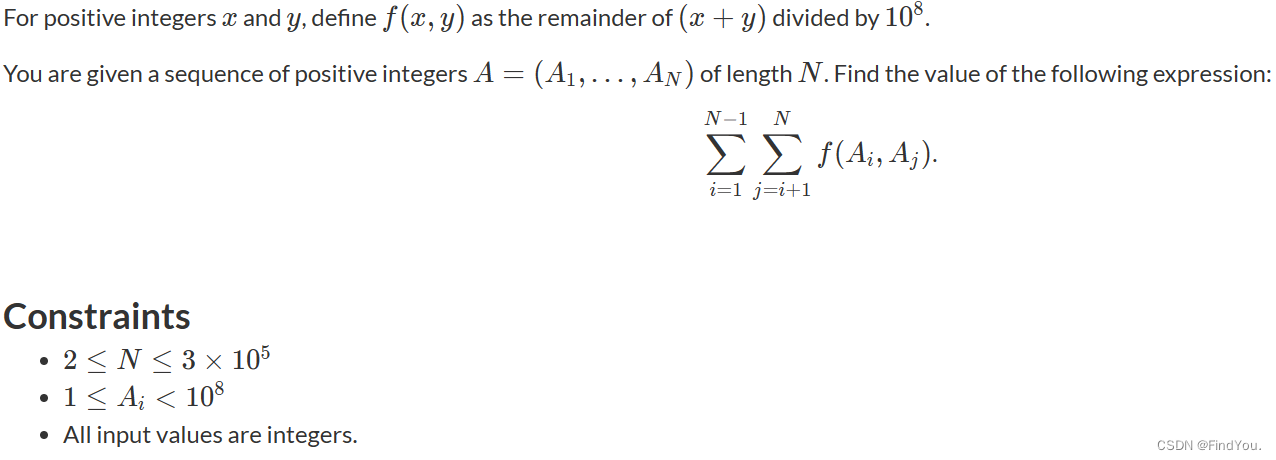
样例：

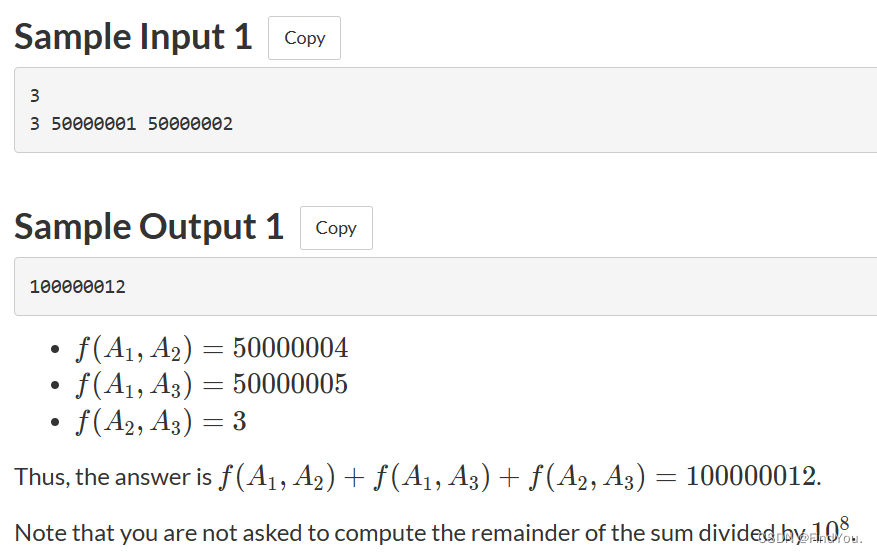题目大致含意:

给你n个数，让你对这n个数进行操作，比如当前是第i个，那么让a[i] 和后面的每个数进行相加,
例如a[i] + a[i + 1] 注意的是a[i] + a[i + 1]的结果要进行取模同理进行操作 (a[i] + a[i + 2]) % mod 输出的结果是把这些运算后的数加起来注意的是 这些加起来的数就不再进行取模操作了

分析：

本题考查的是取模的一些操作，可以先考虑先不去取模着，先把这些结果加在一起这需要利用前缀和的思想推导的公式是: ret += (n - i) * a[i] + (sum[n] - sum[i]); 前提是先把前缀和给提前预处理好，然后取模取模其实就是减去多个 mod，要去知道是哪些(a[i] + a[j]) 他们是大于1e8了然后我再减去就可以了那怎么快速知道有多少个(a[i] + a[j])是大于1e8的！可以枚举每个a[i] 然后二分找到第一个大于等于(1e8 - a[i])的数的位置那么(n - 这个位置)就是这n个数里面和当前的a[i] 相加是大于1e8的那么我就直接ret - 1e8*个数

代码:

// package AtCoderBeginnerContest353;import java.util.Arrays;
import java.util.Scanner;public class C {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();long mod = (long) 1e8;long ret = 0;long[] a = new long[n + 10];long[] sum = new long[n + 10];//就是二分for(int i = 1; i <= n; i ++ ) {a[i] = sc.nextLong();// 也是要利用前缀和的思想sum[i] = sum[i - 1];sum[i] += a[i];}for(int i = 1; i <= n; i ++ ) {ret += (n - i) * a[i] + (sum[n] - sum[i]);}//	System.out.println("ret = " + ret); // ret出现了问题Arrays.sort(a, 1, n + 1);
//		for(int i = 1; i <= n; i ++ ) {
//			System.out.print(a[i] + " ");
//		}for(int i = 1; i <= n; i ++ ) {int l = i, r = n + 1;long x = mod - a[i]; // 这个是要找的 找到第一个大于等于x的位置while(l + 1 < r) {int mid = l + r >> 1;if(a[mid] < x)l = mid;else r = mid;}//System.out.println("i = " + i + " l = " + l);// l + 1 是最后的答案ret -= (mod * (n - l));}System.out.print(ret);}
}