算法刷题笔记数的范围（C++实现）（二分法重要例题）

本文主要是介绍算法刷题笔记数的范围（C++实现）（二分法重要例题），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

- 题目描述
- 题目思路
- 题目代码（C++）
- 题目感想

题目描述

给定一个按照升序排列的长度为n的整数数组，以及q个查询。
对于每个查询，返回一个元素k的起始位置和终止位置（位置从0开始计数）。
如果数组中不存在该元素，则返回 -1 -1。

输入格式：

第一行包含整数n和q，表示数组长度和询问个数。
第二行包含n个整数（均在1∼10000范围内），表示完整数组。
接下来q行，每行包含一个整数k，表示一个询问元素。

输出格式：

共q行，每行包含两个整数，表示所求元素的起始位置和终止位置。
如果数组中不存在该元素，则返回 -1 -1。

题目思路

本题实际上是一个整数二分问题，相当于从一个有序数组中找到两个边界，正好可以用二分查找方法进行解决。
首先，需要找到左边界，即指定的查询数字在数组中的最靠前的出现位置。因此，只需要以中点为参考，判断中点是否满足大于等于需要查询的数值，然后分情况设置下一个区间即可。重复这种情况，直到左右端点重合，则返回此时的点。
- 如果中点对应的值确实大于等于需要查询的数值，则说明需要查询的数值在以中点为划分的左半边区间内（这个区间包含了上一步的中点），因此将区间的右端点修改为当前的中心点。
- 如果中点对应的值小于需要查询的数值，则说明需要查询的数值在以中点为划分的右半区间内（这个区间不包含中点，因为中点的值小于查找的值），因此将区间的左端点设置为当前中心点右边的第一个端点即可。

为什么判定条件是大于等于而不是小于等于：如果采用小于等于，则会将原始的有序数组划分为大于等于查询值和小于查询值的两部分，此时，每一次如果中点小于等于当前查询的值，那么左端点可能在中点的右边（即中点实际是小于查询值的）或中点的左边（查询值有多个位置，中点并非最靠左的一个），因此无法继续二分。

为什么判定条件不使用大于或小于：以大于为例，如果采用大于，则会将原始的有序数组划分为大于查询值和小于等于查询值的两部分。此时，每一次如果中点大于当前查询的值，一定可以判定待查询的值一定在左半边区间内，但是如果中点小于等于查询值，则无法判定左边界的位置，因为左边界可能在中点左边（当中点等于查询值，且不是排在最前面的时候）或中点右边（中点小于查询值时）。

如果此时返回的端点仍然不等于需要查找的值，说明原始数组中不存在和需要查找的值相等的元素，输出 -1 -1；否则，继续进行后续的步骤。
后续步骤即为找出区间的右端点。与找出左端点类似，但是将条件修改为判断中点是否满足小于等于需要查询的数值。当中点小于等于需要查询的数值的时候，说明其一定在以右边界为轴点的左边区间中，因此将区间的左端点设置为右边界即可；当中点大于需要查询的数值的时候，说明其一定在以右边界为轴点（不包括右边界）的右边区间中，因此将区间的右端点设置为中点向左移动一个单位后的端点即可。

题目代码（C++）

#include <cstdio>int n,q;
const int N(1e5 + 10);
int arr[N];
int query;int main(void)
{scanf("%d %d", &n, &q);for(int i(0); i < n; ++i) scanf("%d", &arr[i]);for(int i(0); i < q; ++i) {scanf("%d", &query);int left(0), right(n - 1);while(left < right){int mid((left + right) >> 1);if(arr[mid] >= query) right = mid;else left = mid + 1;}if(arr[left] != query) printf("-1 -1\n");else{printf("%d ",left);left = 0, right = n - 1;while(left < right){int mid((left + right + 1) >> 1);if(arr[mid] <= query) left = mid;else right = mid - 1;}printf("%d\n", right);}}return 0;
}

题目感想

整数二分算法的模板中，需要注意如果是满足条件需要将左边界修改为区间中点（即left = mid），则进行中点位置计算时需要额外加1，否则会出现死循环。
二分的最大难点在于判断使用什么中点判定条件，如上代码所示。
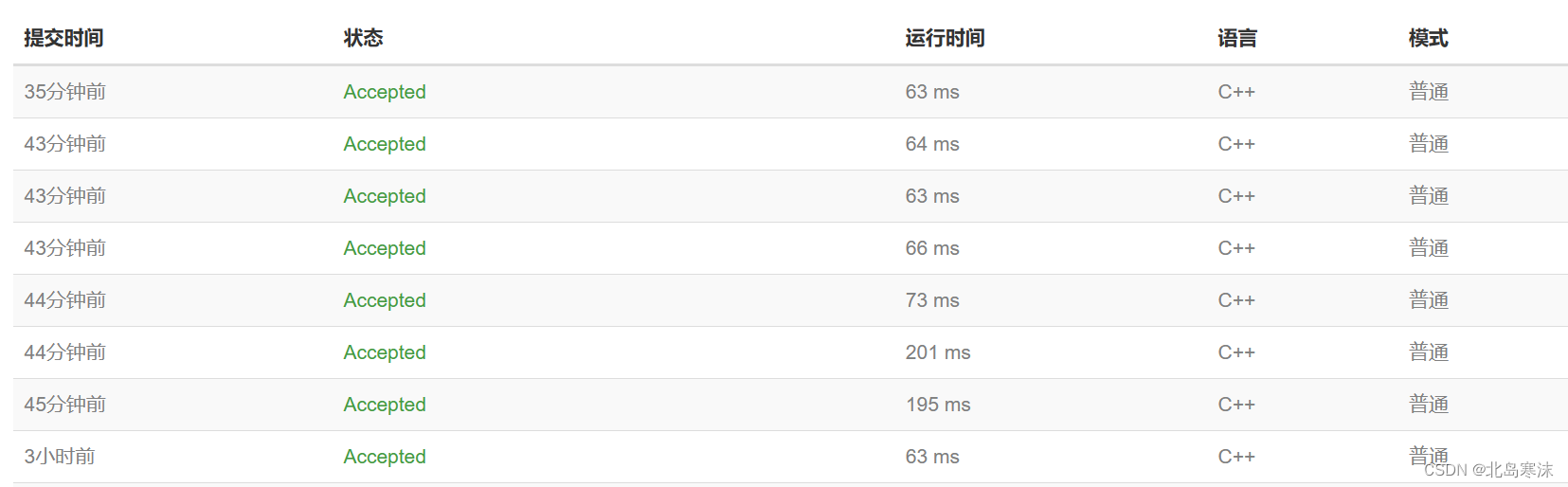
尝试将代码中的所有scanf函数修改为C++中的cin输入方式，发现运行时间天差地别，如下图所示。图中所有两位数的运行时间都是使用scanf得到的结果，三位数的运行时间都是cin得到的结果。