HNU-算法设计与分析-作业6

2024-05-16 11:04
文章标签 算法 分析 设计 作业 hnu

本文主要是介绍HNU-算法设计与分析-作业6，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第六次作业【分支限界法】

在这里插入图片描述

文章目录

    • 第六次作业【分支限界法】
      • <1> 算法实现题6-2 最小权顶点覆盖问题
      • <2> 算法实现题6-6 n后问题
      • <3> 算法实现题6-7 布线问题

<1> 算法实现题6-2 最小权顶点覆盖问题

▲问题重述

问题描述：
给定一个赋权无向图 G=(V,E)，每个顶点 v∈V 都有一个权值 w(v)。如果 U⊆VU⊆V，且对任意(u,v)∈E 有 u∈U 或 v∈U，就称 U 为图 G 的一个顶点覆盖。G 的最小权顶点覆盖是指 G 中所含顶点权之和最小的顶点覆盖。

算法设计：
对于给定的无向图 G，设计一个优先队列式分支限界法，计算 G 的最小权顶点覆盖。

数据输入：
由文件input.txt给出输入数据。第 1 行有 2 个正整数 n 和 m，表示给定的图 G 有 n 个顶点和 m 条边，顶点编号为 1，2，…，n。第 2 行有 n 个正整数表示 n 个顶点的权。接下来 的 m 行中，每行有 2 个正整数 u,v，表示图 G 的一条边(u,v)。

结果输出：
将计算的最小权顶点覆盖的顶点权之和以及最优解输出到文件output.txt。文件的第1行是最小权顶点覆盖顶点权之和；第2行是最优解xi（1<=i<=n）,xi=0表示顶点i不在最小权顶点覆盖中，xi=1表示顶点i在最小权顶点覆盖中。

输入文件示例
input.txt
7 7
1 100 1 1 1 100 10
1 6
2 4
2 5
3 6
4 5
4 6
6 7输出文件示例
output.txt
13
1 0 1 0 1 0 1

▲解题思路

  1. 定义一个最小堆 MinHeap 类，用于实现堆操作。
  2. HeapNode 类表示图中的一个顶点。DealNode 类包含一些操作，主要是用于处理堆中结点的操作。
  3. DealNode::BBVC() 方法是该算法的核心部分。通过不断地加入和不加入某个顶点，并通过堆来遍历所有可能的情况，找到图的最小顶点覆盖。
  4. MinCover 函数是对 DealNode::BBVC() 方法的封装，用于获取最终的最小顶点覆盖权重。
  5. 在 main 函数中，用户输入了图的顶点数 vertexNum 和边数 edgeNum。然后输入每个顶点的权值，并通过边的信息构建了图的邻接矩阵。
  6. 调用 MinCover 函数得到最小顶点覆盖权重，并输出结果。

▲代码

#include <fstream>
#include <iostream>
using namespace std;template <class Type>
class MinHeap // 最小堆类；
{
public:MinHeap(Type a[], int n);   // 带两参数的构造函数，在此程序中没有应用；MinHeap(int ms);            // 构造函数重载，只初始化堆的大小，对堆中结点不初始化；另外，堆元素的存储是以数组~MinHeap();                 // 形式，且无父、子指针，访问父亲结点，利用数组标号进行；bool Insert(const Type &x); // 插入堆中一个元素；bool RemoveMin(Type &x);    // 删除堆顶最小结点；void MakeEmpty();           // 使堆为空bool IsEmpty();bool IsFull();int Size();protected:void FilterDown(const int start, const int endOfHeap); // 自顶向下构造堆void FilterUp(const int start);                        // 自底向上构造堆
private:Type *heap;int maxSize;const int defaultSize;int currentSize; // 堆当前结点个数大小
};template <class Type>
MinHeap<Type>::MinHeap(int ms) : defaultSize(100)
{maxSize = (ms > defaultSize) ? ms : defaultSize;heap = new Type[maxSize];currentSize = 0;
}template <class Type>
MinHeap<Type>::MinHeap(Type a[], int n) : defaultSize(100)
{maxSize = (n > defaultSize) ? n : defaultSize;heap = new Type[maxSize];currentSize = n;for (int i = 0; i < n; i++)heap[i] = a[i];int curPos = (currentSize - 2) / 2;while (curPos >= 0){FilterDown(curPos, currentSize - 1);curPos--;}
}template <class Type>
MinHeap<Type>::~MinHeap()
{delete[] heap;
}template <class Type>
void MinHeap<Type>::FilterDown(const int start, const int endOfHeap)
{int i = start, j = i * 2 + 1;Type temp = heap[i];while (j <= endOfHeap){if (j < endOfHeap && heap[j] > heap[j + 1])j++;if (temp < heap[j])break;else{heap[i] = heap[j];i = j;j = 2 * i + 1;}}heap[i] = temp;
}template <class Type>
void MinHeap<Type>::FilterUp(const int start)
{int i = start, j = (i - 1) / 2;Type temp = heap[i];while (i > 0){if (temp >= heap[j])break;else{heap[i] = heap[j];i = j;j = (i - 1) / 2;}}heap[i] = temp;
}template <class Type>
bool MinHeap<Type>::RemoveMin(Type &x)
{if (IsEmpty()){cerr << "Heap empty!" << endl;return false;}x = heap[0];heap[0] = heap[currentSize - 1];currentSize--;FilterDown(0, currentSize - 1);return true;
}template <class Type>
bool MinHeap<Type>::Insert(const Type &x)
{if (IsFull()){cerr << "Heap Full!" << endl;return false;}heap[currentSize] = x;FilterUp(currentSize);currentSize++;return true;
}template <class Type>
bool MinHeap<Type>::IsEmpty()
{return currentSize == 0;
}template <class Type>
bool MinHeap<Type>::IsFull()
{return currentSize == maxSize;
}template <class Type>
void MinHeap<Type>::MakeEmpty()
{currentSize = 0;
}template <class Type>
int MinHeap<Type>::Size()
{return currentSize;
}// 最小堆结点
class HeapNode // 堆结点类；
{friend class DealNode;public:operator int() const { return cn; }private:int i,  // i标示堆中结点号cn, // cn标示当前加入的覆盖顶点中权重之和*x, // x数组标示那些顶点加入了覆盖顶点的行列*c; // c数组标示X中的覆盖顶点中所有的邻接顶点
};// VC类用来对堆中结点内部的的操作
class DealNode
{friend int MinCover(int **, int[], int);private:void BBVC();bool cover(HeapNode E);void AddLiveNode(MinHeap<HeapNode> &H, HeapNode E, int cn, int i, bool ch);int **a, n, *w, *bestx, bestn;
};void DealNode::BBVC()
{// 建立初始空堆MinHeap<HeapNode> H(1000);HeapNode E;E.x = new int[n + 1];E.c = new int[n + 1];for (int j = 1; j <= n; j++){E.x[j] = E.c[j] = 0;}int i = 1, cn = 0;while (true){if (i > n){if (cover(E)){for (int j = 1; j <= n; j++)bestx[j] = E.x[j];bestn = cn;break;}}else{if (!cover(E))AddLiveNode(H, E, cn, i, true); // 加入结点标号为i 的结点到顶点覆盖集中，并把更新后的结点再插入堆中AddLiveNode(H, E, cn, i, false);    // 不把结点标号为 i 的结点加入到顶点覆盖集中，并把更新后的结点插入堆中}if (H.IsEmpty())break;H.RemoveMin(E); // 取堆顶点赋给Ecn = E.cn;i = E.i + 1;}
}// 检测图是否被覆盖
bool DealNode::cover(HeapNode E)
{for (int j = 1; j <= n; j++){if (E.x[j] == 0 && E.c[j] == 0) // 存在任意一条边的两个顶点都为0的情况下，为未覆盖情况return false;               // X[j]记录覆盖顶点，c[j]记录与覆盖顶点相连的顶点 0表征未覆盖，1表征已覆盖}return true;
}void DealNode::AddLiveNode(MinHeap<HeapNode> &H, HeapNode E, int cn, int i, bool ch)
{HeapNode N;N.x = new int[n + 1];N.c = new int[n + 1];for (int j = 1; j <= n; j++){N.x[j] = E.x[j];N.c[j] = E.c[j];}N.x[i] = ch ? 1 : 0;if (ch){N.cn = cn + w[i]; // 记录i顶点是否加入覆盖的行列中；for (int j = 1; j <= n; j++)if (a[i][j] > 0) // 如果i,j相邻，刚把j顶点加入覆盖邻接顶点集中；N.c[j]++;}else{N.cn = cn;}N.i = i;H.Insert(N); // 插入堆中
}int MinCover(int **a, int v[], int n)
{DealNode Y;Y.w = new int[n + 1];for (int j = 1; j <= n; j++){Y.w[j] = v[j]; // 初始化DealNode类对象Y;}Y.a = a;Y.n = n;Y.bestx = v; // 将地址赋予bestx，Y.BBVC();return Y.bestn; // bestn是最后的最小顶点覆盖集权重；
}int main()
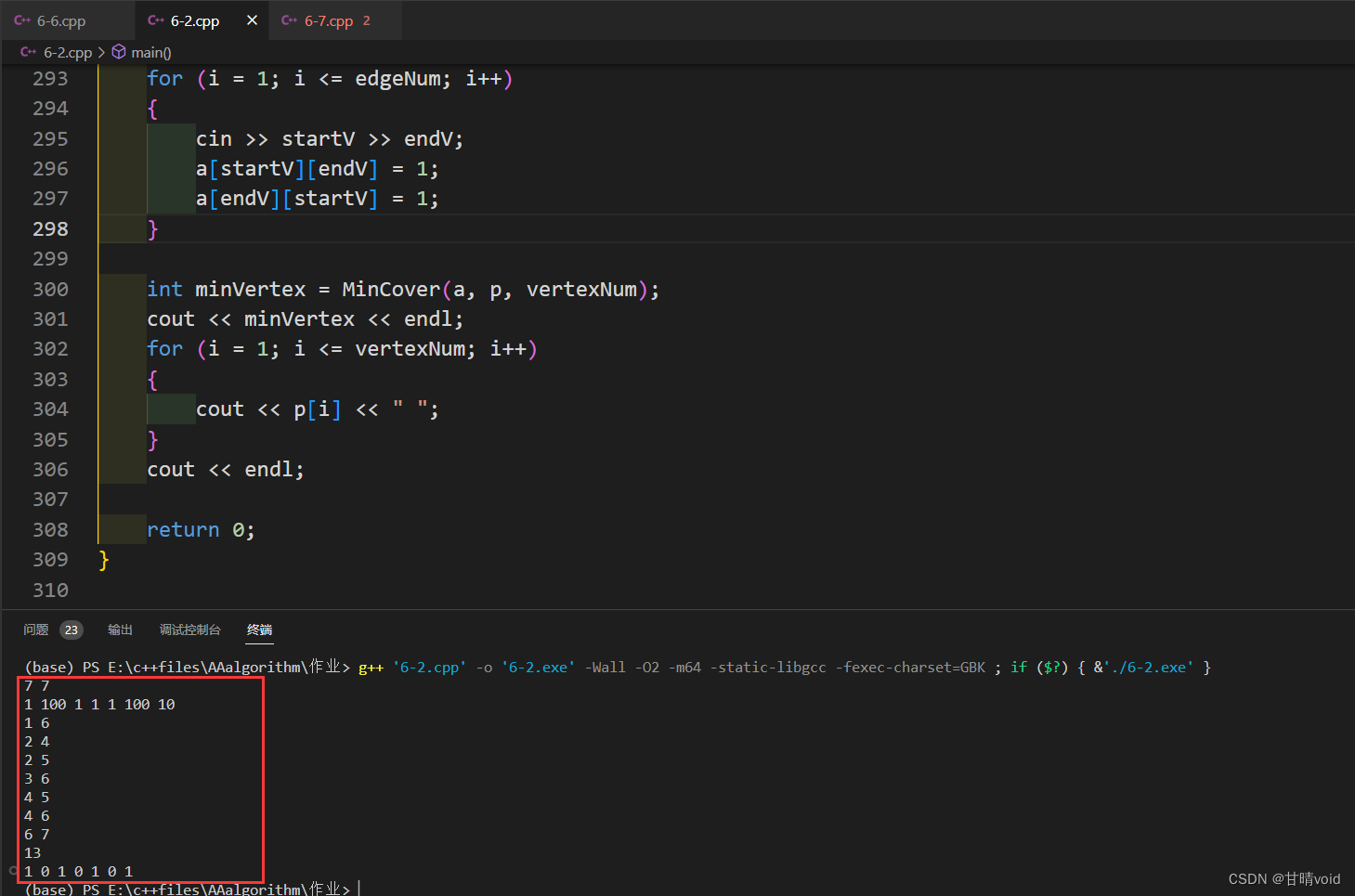
{int startV, endV;       // 一条边的起始节点，终止节点int vertexNum, edgeNum; // 顶点数，边数int i;cin >> vertexNum >> edgeNum;int **a; // 图的邻接矩阵表示，1表示有边a = new int *[vertexNum + 1];for (int k = 0; k <= vertexNum; k++)a[k] = new int[vertexNum + 1];for (int i = 0; i <= vertexNum; i++)for (int j = 0; j <= vertexNum; j++)a[i][i] = 0;int *p; // 顶点的权值数组p = new int[vertexNum + 1];for (i = 1; i <= vertexNum; i++)cin >> p[i];for (i = 1; i <= edgeNum; i++){cin >> startV >> endV;a[startV][endV] = 1;a[endV][startV] = 1;}int minVertex = MinCover(a, p, vertexNum);cout << minVertex << endl;for (i = 1; i <= vertexNum; i++){cout << p[i] << " ";}cout << endl;return 0;
}

▲验证

在这里插入图片描述

<2> 算法实现题6-6 n后问题

▲问题重述

设计一个解n后问题的队列式分支限界法，计算在n × n n\times nn×n个方格上放置彼此不受攻击的n个皇后的一个放置方案。
案例

input
5
output
1 3 5 2 4

▲解题思路

  1. 定义一个结构体node，表示棋盘上的每一个可能的位置，以及记录了当前状态的一些信息，如列、左右对角线等的占用情况。
  2. 使用优先队列priority_queue来存储搜索过程中的状态，按照结构体中的x值进行排序。这里的x表示当前放置的皇后所在的行数。
  3. 在主循环中，初始化棋盘的初始状态，将第一行的每一个位置作为起点，生成相应的初始状态，并加入优先队列中。
  4. 进入主循环，每次从优先队列中取出一个状态，判断是否达到了目标状态（即放置了所有皇后），如果是则输出解，并结束程序（因为只需要找到一个可行解即可）。
  5. 如果当前状态不是目标状态，继续在下一行尝试放置皇后。遍历每一列，对于每一个可行的位置，生成新的状态并加入优先队列中。
  6. 在生成新状态时，进行剪枝操作，检查当前位置是否与之前的皇后冲突，如果冲突则跳过该位置。
  7. 重复以上步骤，直到找到一个解或者队列为空。由于采用优先队列，搜索时会先尝试最有希望的位置，加速找到解的过程。

▲代码

#include <bits/stdc++.h>
using namespace std;
#define N 100
int n;
struct node
{int vis[N] = {0}, col[N] = {0}, lr[N] = {0}, rl[N] = {0};int x, y;node(int a, int b) : x(a), y(b) {}bool operator<(const node &a) const{return x < a.x;}
};
priority_queue<node> q;
int main()
{cin >> n;for (int i = 0; i < n; i++){node temp = node(0, i);temp.vis[0] = i + 1;temp.col[i] = 1;temp.rl[temp.x + temp.y] = 1;temp.lr[50 + temp.x - temp.y] = 1;q.push(temp);}while (!q.empty()){node temp = q.top();q.pop();if (temp.x == n - 1){for (int i = 0; i < n; i++){cout << temp.vis[i] << " ";}cout << endl;break; // 只需要给出一个答案即可}if (temp.x < n - 1){for (int i = 0; i < n; i++){node next = node(temp.x + 1, i);if (temp.col[next.y] || temp.lr[50 + next.x - next.y] || temp.rl[next.x + next.y]){ // 剪枝continue;}for (int i = 0; i < N; i++){next.lr[i] = temp.lr[i];next.rl[i] = temp.rl[i];next.col[i] = temp.col[i];}next.col[next.y] = 1;next.lr[50 + next.x - next.y] = 1;next.rl[next.x + next.y] = 1;for (int i = 0; i < next.x; i++){next.vis[i] = temp.vis[i];}next.vis[next.x] = i + 1;q.push(next);}}}return 0;
}

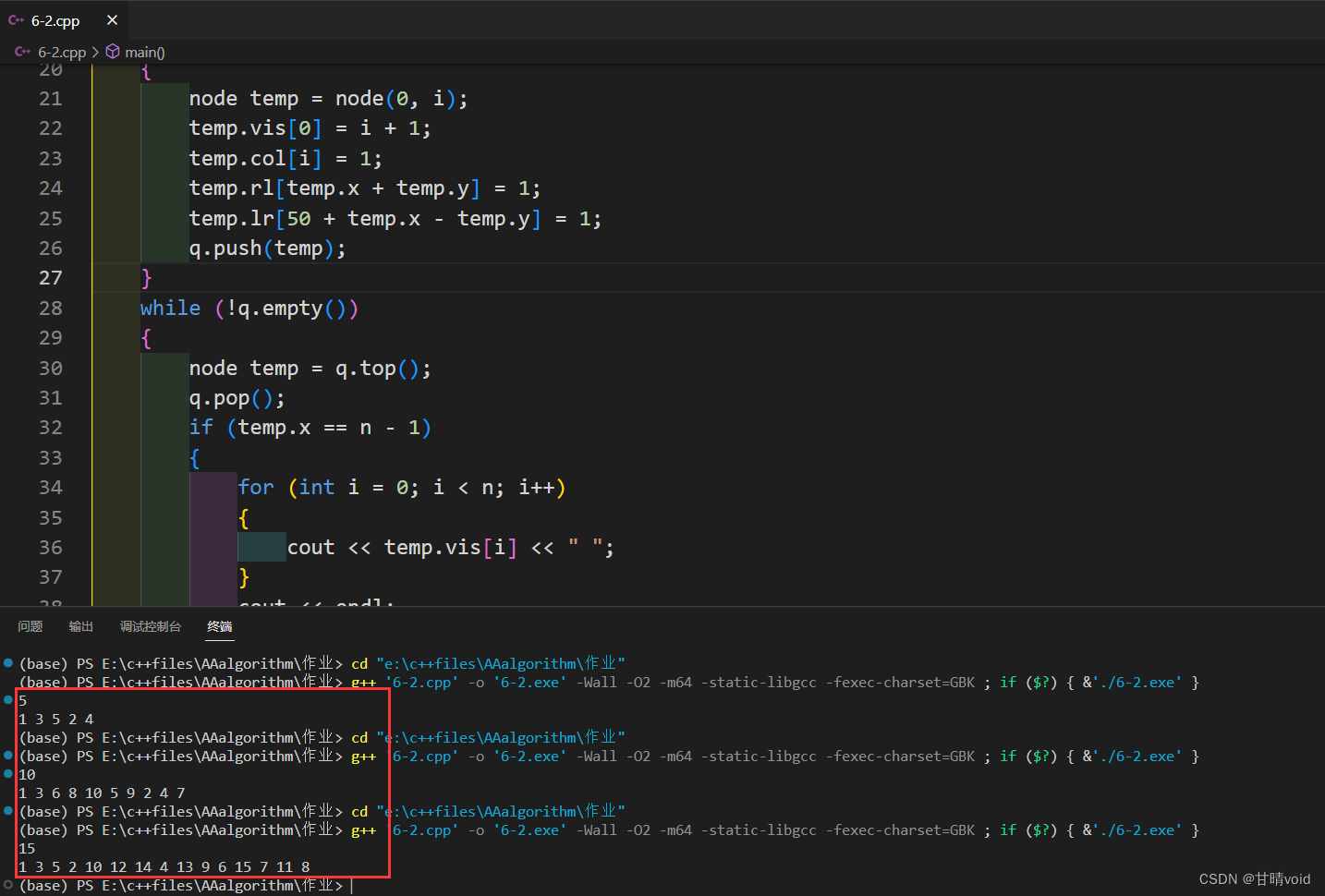
▲验证

验证了n=5,10,15三种情况。

在这里插入图片描述

<3> 算法实现题6-7 布线问题

▲问题重述

在这里插入图片描述

▲解题思路

  1. MinHeap 类定义了最小堆，用于存储待处理的状态。该堆的元素是 BoardNode 类型的对象。
  2. BoardNode 类表示电路板的一种摆放方式，包含了一些必要的信息。len 方法用于计算电路板摆放的长度。
  3. BBArrangeBoards 函数是基于分支限界法的核心算法。它通过不断生成摆放状态，使用最小堆来搜索可能的最优解。HeapSize 为堆的大小。
  4. Make2DArray 函数用于动态创建二维数组。
  5. 在 main 函数中，用户输入了电路板数量 n。通过 Make2DArray 创建了二维数组 B，表示电路板之间的连接关系。然后调用 BBArrangeBoards 函数求解问题，并输出最小长度和对应的摆放方式。

▲代码

#include <array>
#include <bits/stdc++.h>
#include <queue>
using namespace std;
int n, *p;
template <class Type>
class MinHeap // 最小堆类；
{
public:MinHeap(Type a[], int n);   // 带两参数的构造函数，在此程序中没有应用；MinHeap(int ms);            // 构造函数重载，只初始化堆的大小，对堆中结点不初始化；另外，堆元素的存储是以数组~MinHeap();                 // 形式，且无父、子指针，访问父亲结点，利用数组标号进行；bool Insert(const Type &x); // 插入堆中一个元素；bool RemoveMin(Type &x);    // 删除堆顶最小结点；void MakeEmpty();           // 使堆为空bool IsEmpty();bool IsFull();int Size();protected:void FilterDown(const int start, const int endOfHeap); // 自顶向下构造堆void FilterUp(const int start);                        // 自底向上构造堆
private:Type *heap;int maxSize;const int defaultSize;int currentSize; // 堆当前结点个数大小
};template <class Type>
MinHeap<Type>::MinHeap(int ms) : defaultSize(100)
{maxSize = (ms > defaultSize) ? ms : defaultSize;heap = new Type[maxSize];currentSize = 0;
}template <class Type>
MinHeap<Type>::MinHeap(Type a[], int n) : defaultSize(100)
{maxSize = (n > defaultSize) ? n : defaultSize;heap = new Type[maxSize];currentSize = n;for (int i = 0; i < n; i++)heap[i] = a[i];int curPos = (currentSize - 2) / 2;while (curPos >= 0){FilterDown(curPos, currentSize - 1);curPos--;}
}template <class Type>
MinHeap<Type>::~MinHeap()
{delete[] heap;
}template <class Type>
void MinHeap<Type>::FilterDown(const int start, const int endOfHeap)
{int i = start, j = i * 2 + 1;Type temp = heap[i];while (j <= endOfHeap){if (j < endOfHeap && heap[j] > heap[j + 1])j++;if (temp < heap[j])break;else{heap[i] = heap[j];i = j;j = 2 * i + 1;}}heap[i] = temp;
}template <class Type>
void MinHeap<Type>::FilterUp(const int start)
{int i = start, j = (i - 1) / 2;Type temp = heap[i];while (i > 0){if (temp >= heap[j])break;else{heap[i] = heap[j];i = j;j = (i - 1) / 2;}}heap[i] = temp;
}template <class Type>
bool MinHeap<Type>::RemoveMin(Type &x)
{if (IsEmpty()){cerr << "Heap empty!" << endl;return false;}x = heap[0];heap[0] = heap[currentSize - 1];currentSize--;FilterDown(0, currentSize - 1);return true;
}template <class Type>
bool MinHeap<Type>::Insert(const Type &x)
{if (IsFull()){cerr << "Heap Full!" << endl;return false;}heap[currentSize] = x;FilterUp(currentSize);currentSize++;return true;
}template <class Type>
bool MinHeap<Type>::IsEmpty()
{return currentSize == 0;
}template <class Type>
bool MinHeap<Type>::IsFull()
{return currentSize == maxSize;
}template <class Type>
void MinHeap<Type>::MakeEmpty()
{currentSize = 0;
}template <class Type>
int MinHeap<Type>::Size()
{return currentSize;
}class BoardNode
{friend int BBArrangeBoards(int **, int, int *&);public:operator int() const { return cd; }int len(int **, int ii);private:int *x, s, cd;
};int BoardNode::len(int **conn, int ii)
{int sum = 0;for (int i = 1, sum = 0; i <= ii; i++){for (int j = i + 1; j <= ii; j++){int dist = x[i] > x[j] ? x[i] - x[j] : x[j] - x[i];sum += conn[i][j] * dist;}}return sum;
}int BBArrangeBoards(int **conn, int n, int *&bestx)
{int HeapSize = 10;MinHeap<BoardNode>H(HeapSize);BoardNode E;E.x = new int[n + 1];E.s = 0;E.cd = 0;for (int i = 1; i <= n; i++)E.x[i] = i;int bestd = INT_MAX;bestx = 0;while (E.cd < bestd){if (E.s == n - 1){int ld = E.len(conn, n);if (ld < bestd){delete[] bestx;bestx = E.x;bestd = ld;}elsedelete[] E.x;}else{for (int i = E.s + 1; i <= n; i++){BoardNode N;N.x = new int[n + 1];N.s = E.s + 1;for (int j = 1; j <= n; j++)N.x[j] = E.x[j];N.x[N.s] = E.x[i];N.x[i] = E.x[N.s];N.cd = N.len(conn, N.s);if (N.cd < bestd)H.Insert(N);elsedelete[] N.x;}}delete[] E.x;}try{H.RemoveMin(E);}catch (...){return bestd;}while (true){delete[] E.x;try{H.RemoveMin(E);}catch (...){break;}}return bestd;
}template <class T>
void Make2DArray(T **&x, int rows, int cols)
{x = new T *[rows];for (int i = 0; i < rows; ++i){x[i] = new T[cols];}
}int main()
{cin >> n;p = new int[n + 1];int **B;Make2DArray(B, n + 1, n + 1);for (int i = 1; i <= n - 1; i++)for (int j = i + 1; j <= n; j++)cin >> B[i][j];cout << BBArrangeBoards(B, n, p) << endl;for (int i = 1; i <= n; i++)cout << p[i] << " ";cout << endl;return 0;
}

▲验证

书上案例验证通过。

这篇关于HNU-算法设计与分析-作业6的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/994725。

相关文章

不懂推荐算法也能设计推荐系统

不懂推荐算法也能设计推荐系统

本文以商业化应用推荐为例，告诉我们不懂推荐算法的产品，也能从产品侧出发， 设计出一款不错的推荐系统。 相信很多新手产品，看到算法二字，多是懵圈的。 什么排序算法、最短路径等都是相对传统的算法（注：传统是指科班出身的产品都会接触过）。但对于推荐算法，多数产品对着网上搜到的资源，都会无从下手。特别当某些推荐算法 和 “AI”扯上关系后，更是加大了理解的难度。 但，不了解推荐算法，就无法做推荐系
阅读更多...
作业提交过程之HDFSMapReduce

作业提交过程之HDFSMapReduce

作业提交全过程详解 （1）作业提交 第1步：Client调用job.waitForCompletion方法，向整个集群提交MapReduce作业。 第2步：Client向RM申请一个作业id。 第3步：RM给Client返回该job资源的提交路径和作业id。 第4步：Client提交jar包、切片信息和配置文件到指定的资源提交路径。 第5步：Client提交完资源后，向RM申请运行MrAp
阅读更多...
康拓展开（hash算法中会用到）

康拓展开（hash算法中会用到）

康拓展开是一个全排列到一个自然数的双射（也就是某个全排列与某个自然数一一对应） 公式： X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0! 其中,a[i]为整数,并且0<=a[i]<i,1<=i<=n。（a[i]在不同应用中的含义不同）； 典型应用： 计算当前排列在所有由小到大全排列中的顺序，也就是说求当前排列是第
阅读更多...
性能分析之MySQL索引实战案例

性能分析之MySQL索引实战案例

文章目录 一、前言二、准备三、MySQL索引优化四、MySQL 索引知识回顾五、总结 一、前言 在上一讲性能工具之 JProfiler 简单登录案例分析实战中已经发现SQL没有建立索引问题，本文将一起从代码层去分析为什么没有建立索引？ 开源ERP项目地址：https://gitee.com/jishenghua/JSH_ERP 二、准备 打开IDEA找到登录请求资源路径位置
阅读更多...
csu 1446 Problem J Modified LCS （扩展欧几里得算法的简单应用）

csu 1446 Problem J Modified LCS （扩展欧几里得算法的简单应用）

这是一道扩展欧几里得算法的简单应用题，这题是在湖南多校训练赛中队友ac的一道题，在比赛之后请教了队友，然后自己把它a掉 这也是自己独自做扩展欧几里得算法的题目 题意：把题意转变下就变成了：求d1*x - d2*y = f2 - f1的解,很明显用exgcd来解 下面介绍一下exgcd的一些知识点：求ax + by = c的解 一、首先求ax + by = gcd(a,b)的解 这个
阅读更多...
综合安防管理平台LntonAIServer视频监控汇聚抖动检测算法优势

综合安防管理平台LntonAIServer视频监控汇聚抖动检测算法优势

LntonAIServer视频质量诊断功能中的抖动检测是一个专门针对视频稳定性进行分析的功能。抖动通常是指视频帧之间的不必要运动，这种运动可能是由于摄像机的移动、传输中的错误或编解码问题导致的。抖动检测对于确保视频内容的平滑性和观看体验至关重要。 优势 1. 提高图像质量 - 清晰度提升：减少抖动，提高图像的清晰度和细节表现力，使得监控画面更加真实可信。 - 细节增强：在低光条件下，抖
阅读更多...
【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

前言：快速排序的实现最重要的是找基准值，下面让我们来了解如何实现找基准值 基准值的注释：在快排的过程中，每一次我们要取一个元素作为枢纽值，以这个数字来将序列划分为两部分。 在此我们采用三数取中法，也就是取左端、中间、右端三个数，然后进行排序，将中间数作为枢纽值。 快速排序实现主框架： //快速排序 void QuickSort(int* arr, int left, int rig
阅读更多...
poj 3974 and hdu 3068 最长回文串的O（n）解法(Manacher算法)

poj 3974 and hdu 3068 最长回文串的O（n）解法(Manacher算法)

求一段字符串中的最长回文串。 因为数据量比较大，用原来的O（n^2）会爆。 小白上的O(n^2)解法代码：TLE啦~ #include<stdio.h>#include<string.h>const int Maxn = 1000000;char s[Maxn];int main(){char e[] = {"END"};while(scanf("%s", s) != EO
阅读更多...
秋招最新大模型算法面试，熬夜都要肝完它

秋招最新大模型算法面试，熬夜都要肝完它

💥大家在面试大模型LLM这个板块的时候，不知道面试完会不会复盘、总结，做笔记的习惯，这份大模型算法岗面试八股笔记也帮助不少人拿到过offer ✨对于面试大模型算法工程师会有一定的帮助，都附有完整答案，熬夜也要看完，祝大家一臂之力 这份《大模型算法工程师面试题》已经上传CSDN，还有完整版的大模型 AI 学习资料，朋友们如果需要可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费
阅读更多...
怎么让1台电脑共享给7人同时流畅设计

怎么让1台电脑共享给7人同时流畅设计

在当今的创意设计与数字内容生产领域，图形工作站以其强大的计算能力、专业的图形处理能力和稳定的系统性能，成为了众多设计师、动画师、视频编辑师等创意工作者的必备工具。 设计团队面临资源有限，比如只有一台高性能电脑时，如何高效地让七人同时流畅地进行设计工作，便成为了一个亟待解决的问题。 一、硬件升级与配置 1.高性能处理器（CPU）：选择多核、高线程的处理器，例如Intel的至强系列或AMD的Ry
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2