HNU-算法设计与分析-作业2

2024-05-16 06:36
文章标签 算法 分析 设计 作业 hnu

本文主要是介绍HNU-算法设计与分析-作业2，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第二次作业【分治算法】

在这里插入图片描述

文章目录

    • 第二次作业【分治算法】
      • <1>算法实现题 2-2 马的Hamilton周游路线问题
      • <2> 算法实现题 2-3 半数集问题
      • <3>算法实现题 2-6 排列的字典序问题
      • <4> 算法实现题 2-7 集合划分问题

<1>算法实现题 2-2 马的Hamilton周游路线问题

▲题目重述

8*8的国际象棋棋盘上的一只马，恰好走过除起点外的其他63个位置各一次，最后回到起点。这条路线称为马的一条Hamiltion周游路线。对于给定的m*n的国际象棋盘，m,n均为大于5的偶数，且|m-n|<=2,试分析分治算法找出马的一条Hamilton周游路线。

算法设计：对于给定的偶数m,n>=6,且|m-n|<=2,计算m*n的国际象棋盘上马的一条Hamilton周游路线。
数据输入：由文件input.txt给出输入数据。第1行有两个正整数m和n,表示给固定的国际象棋棋盘有m行，每行有n个格子组成
结果输出：将计算的马的Hamilton周游路线用下面两种表达方式输出到文件output.txt.

▲解题思路

首先打表数据*：66,68,88,810,1010,1012的结构化棋盘，其中是小规模的子结构，其中包含了该规模的棋盘走法。

分治划分规模：将棋盘尽可能平均地分割成4块。当m,n=4k时，分割为2个2k；当m,n=4k+2时，分割为1个2k和1个2k+2，如图：

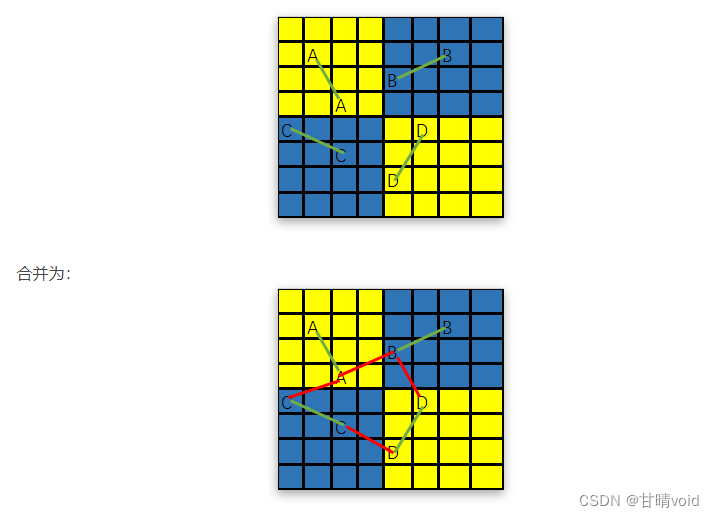
在这里插入图片描述

▲代码

#include <iostream>
#include <fstream>
using namespace std;
struct grid
{//表示坐标int x;int y;
};
class Knight{public:Knight(int m,int n);~Knight(){};void out0(int m,int n,ofstream &out);grid *b66,*b68,*b86,*b88,*b810,*b108,*b1010,*b1012,*b1210,link[20][20];int m,n;int pos(int x,int y,int col);void step(int m,int n,int a[20][20],grid *b);void build(int m,int n,int offx,int offy,int col,grid *b);void base0(int mm,int nn,int offx,int offy);bool comp(int mm,int nn,int offx,int offy);
};
Knight::Knight(int mm,int nn){int i,j,a[20][20];m=mm;n=nn;b66=new grid[36];b68=new grid[48];b86=new grid[48];b88=new grid[64];b810=new grid[80];b108=new grid[80];b1010=new grid[100];b1012=new grid[120];b1210=new grid[120];//cout<<"6*6"<<"\n";ifstream in0("66.txt",ios::in); //利用文件流读取数据ifstream in1("68.txt",ios::in); //利用文件流读取数据ifstream in2("88.txt",ios::in); //利用文件流读取数据ifstream in3("810.txt",ios::in); //利用文件流读取数据ifstream in4("1010.txt",ios::in); //利用文件流读取数据ifstream in5("1012.txt",ios::in); //利用文件流读取数据for(i=0;i<6;i++){for(j=0;j<6;j++){in0>>a[i][j];}}step(6,6,a,b66);//cout<<"6*8"<<"\n";for(i=0;i<6;i++){for(j=0;j<8;j++){in1>>a[i][j];}}step(6,8,a,b68);step(8,6,a,b86);//cout<<"8*8"<<"\n";for(i=0;i<8;i++){for(j=0;j<8;j++){in2>>a[i][j];}}step(8,8,a,b88);for(i=0;i<8;i++){for(j=0;j<10;j++){in3>>a[i][j];}}step(8,10,a,b810);step(10,8,a,b108);//cout<<"10*10"<<"\n";for(i=0;i<10;i++){for(j=0;j<10;j++){in4>>a[i][j];}}step(10,10,a,b1010);for(i=0;i<10;i++){for(j=0;j<12;j++){in5>>a[i][j];}}step(10,12,a,b1012);step(12,10,a,b1210);
}
//将读入的基础棋盘的数据转换为网格数据
void Knight::step(int m,int n,int a[20][20],grid *b)
{int i,j,k=m*n;if(m<n){for(i=0;i<m;i++){for(j=0;j<n;j++){int p=a[i][j]-1;b[p].x=i;b[p].y=j;}}}else{for(i=0;i<m;i++){for(j=0;j<n;j++){int p=a[j][i]-1;b[p].x=i;b[p].y=j;}}}
}
//分治法的主体部分
bool Knight::comp(int mm,int nn,int offx,int offy)
{int mm1,mm2,nn1,nn2;int x[8],y[8],p[8];if(mm%2||nn%2||mm-nn>2||nn-mm>2||mm<6||nn<6) return 1;if(mm<12||nn<12){base0(mm,nn,offx,offy);return 0;}mm1=mm/2;if(mm%4>0){mm1--;}mm2=mm-mm1;nn1=nn/2;if(nn%4>0){nn1--;}nn2=nn-nn1;//分割comp(mm1,nn1,offx,offy);//左上角comp(mm1,nn2,offx,offy+nn1);//右上角comp(mm2,nn1,offx+mm1,offy);//左下角comp(mm2,nn2,offx+mm1,offy+nn1);//右下角//合并x[0]=offx+mm1-1; y[0]=offy+nn1-3;x[1]=x[0]-1;     y[1]=y[0]+2;x[2]=x[1]-1;     y[2]=y[1]+2;x[3]=x[2]+2;     y[3]=y[2]-1;x[4]=x[3]+1;     y[4]=y[3]+2;x[5]=x[4]+1;     y[5]=y[4]-2;x[6]=x[5]+1;     y[6]=y[5]-2;x[7]=x[6]-2;     y[7]=y[6]+1;for(int i=0;i<8;i++){p[i]=pos(x[i],y[i],n);}for(int i=1;i<8;i+=2){int j1=(i+1)%8,j2=(i+2)%8;if(link[x[i]][y[i]].x==p[i-1])link[x[i]][y[i]].x=p[j1];elselink[x[i]][y[i]].y=p[j1];if(link[x[j1]][y[j1]].x==p[j2])link[x[j1]][y[j1]].x=p[i];elselink[x[j1]][y[j1]].y=p[i];}return 0;
}
根据基础解构造子棋盘的Hamilton回路
void Knight::base0(int mm,int nn,int offx,int offy)
{if(mm==6&&nn==6)build(mm,nn,offx,offy,n,b66);if(mm==6&&nn==8)build(mm,nn,offx,offy,n,b68);if(mm==8&&nn==6)build(mm,nn,offx,offy,n,b86);if(mm==8&&nn==8)build(mm,nn,offx,offy,n,b88);if(mm==8&&nn==10)build(mm,nn,offx,offy,n,b810);if(mm==10&&nn==8)build(mm,nn,offx,offy,n,b108);if(mm==10&&nn==10)build(mm,nn,offx,offy,n,b1010);if(mm==10&&nn==12)build(mm,nn,offx,offy,n,b1012);if(mm==12&&nn==10)build(mm,nn,offx,offy,n,b1210);
}
void Knight::build(int m,int n,int offx,int offy,int col ,grid *b)
{int i,p,q,k=m*n;for(i=0;i<k;i++){int x1=offx+b[i].x,y1=offy+b[i].y,x2=offx+b[(i+1)%k].x,y2=offy+b[(i+1)%k].y;p=pos(x1,y1,col);q=pos(x2,y2,col);link[x1][y1].x =q;link[x2][y2].y =p;}
}
//计算方格的编号
int Knight::pos(int x,int y,int col)
{return col*x+y;
}
void Knight::out0(int m,int n,ofstream &out)
{int i,j,k,x,y,p,a[20][20];if(comp(m,n,0,0))return;for(i=0;i<m;i++){for(j=0;j<n;j++){a[i][j]=0;}}i=0;j=0;k=2;a[0][0]=1;out<<"(0,0)"<<"";for(p=1;p<m*n;p++){x=link[i][j].x;y=link[i][j].y;i=x/n;j=x%n;if(a[i][j]>0){i=y/n;j=y%n;}a[i][j]=k++;out<<"("<<i<<","<<j<<")";if((k-1)%n==0){out<<"\n";}}out<<"\n";for(i=0;i<m;i++){for(j=0;j<n;j++){out<<a[i][j]<<"   ";}out<<"\n";}
}
int main()
{int m,n;ifstream in("input.txt",ios::in); //利用文件流读取数据ofstream out("output.txt",ios::out);//利用文件流将数据存到文件中in>>m>>n;Knight k(m,n);k.comp(m,n,0,0);k.out0(m,n,out);in.close();out.close();
}

▲验证

书上案例验证通过

<2> 算法实现题 2-3 半数集问题

▲问题重述

给定一个自然数 n，由 n 开始可以依次产生半数集 set(n)中的数如下。

  • (1) n∈set(n)；

  • (2) 在 n 的左边加上一个自然数，但该自然数不能超过最近添加的数的一半；

  • (3) 按此规则进行处理，直到不能再添加自然数为止。

例如，set(6)={6,16,26,126,36,136}。半数集 set(6)中有 6 个元素。
注意半数集是多重集。

编程任务：对于给定的自然数 n，编程计算半数集 set(n)中的元素个数。

数据输入：输入数据由文件名为 input.txt 的文本文件提供。每个文件只有 1 行，给出整数 n。(0<n<1000)

结果输出：程序运行结束时，将计算结果输出到文件 output.txt 中。输出文件只有 1 行，给出半数集 set(n)中的元素个数。

▲解题思路

问题有些复杂的时候可以先举例子。

例如.set(6) 6，16，26，126，36，136。半数集set(6)中有6个元素。

例如.set(10) 10，510，2510，12510，1510，410，2410，12410，1410，310，1310，210，1210，110，半数集set(10)中有14个元素。

设set(n)中的元素个数为f(n)。如：6的前面可以加上1、2、3，而2、3的前面又都可以加上1，也就是f(6)=1+f(3)+f(2)+f(1)。

则显然有递归表达式：f(n)=1+∑f(i)，i=1,2……n/2。

可以先写一个递归函数如下

int f(int n)
{
int temp=1;
if(n>1)
for (int  i=1；i < = n/2；i ++)temp+=f(i)；
return temp；
}

时间复杂度：n/2个相加，每一个需要计算1+…+i/2，因此时间复杂度为O(n^2)缺点：这样会有很多的重复子问题计算。

这个问题显然存在重叠子问题：例如，当n=4时，f(4)=1+f(1)+f(2)，而f(2)=1+f(1)，在计算f(2)的时候又要重复计算一次f(1)。如果这样的话时间复杂度会很大，我们要想办法简化重叠部分的计算。

可以采用“备忘录”的方法，来避免重叠部分的计算。

▲代码

#include <algorithm>
#include <stdio.h>
using namespace std;int solve(int f[], int n)
{if (n == 1)return 1;if (f[n] != 0)return f[n];int sum = 1;for (int i = 1; i <= n / 2; i++)sum += solve(f, i);f[n] = sum;return sum;
}int main()
{int n;scanf("%d", &n);int f[n + 1];for (int i = 1; i <= n; i++)f[i] = 0;printf("%d\n", solve(f, n));
}

▲验证

P1028 [NOIP2001 普及组] 数的计算（https://www.luogu.com.cn/problem/P1028）

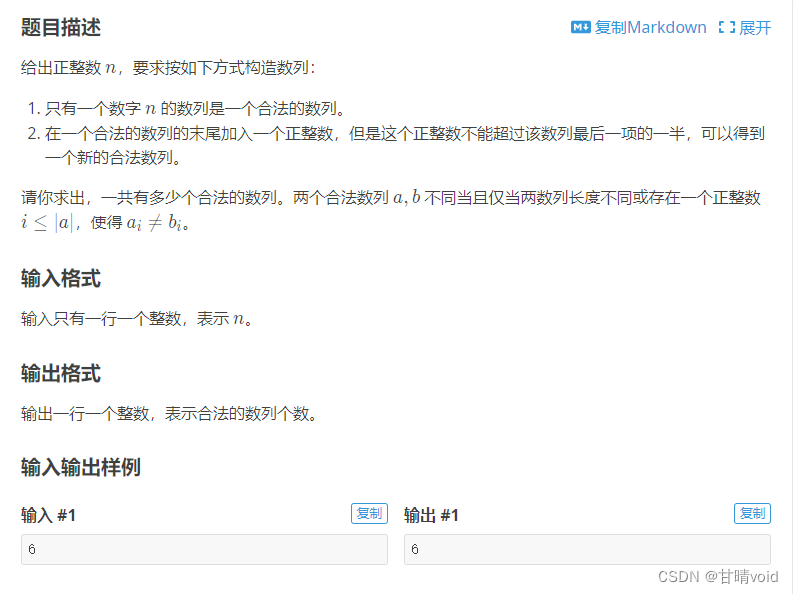
在这里插入图片描述

测试结果如下：

在这里插入图片描述

▲算法分析

使用到记忆化剪枝，本质上仍然是对每个f[i]都去遍历了f[0]到f[n/2]，所以时间复杂度应该是O(n^2)。

由于开了备忘录数组，空间复杂度O(n)。

<3>算法实现题 2-6 排列的字典序问题

▲题目重述

问题描述：n个元素1 , 2 , ⋯   , n 有 n ! {1,2,\cdots,n}有n!1,2,⋯,n有n!个不同的排列。将这n ! n!n!个排列按字典序排列，并编号为0 , 1 , ⋯   , n ! − 1 0,1,\cdots,n!-10,1,⋯,n!−1。每个排列的编号为其字典序值。例如，当n=3时，6个不同排列的字典序值如下：

字典序值012345
排列123132213231312321

算法设计：给点n及n个元素的一个排列，计算出这个排列的字典序值，以及按字典序排列的下一个排列
数据输入：由文件input.txt提供输入数据。文件的第1行是元素个数n。接下来的一行是n个元素的一个排列
结果输出：将计算出的排列的字典序值和按字典序排列的下一个排列输出到文件output.txt。文件的第1行是字典序值，第2行是按字典序排列的下一个排列。

▲解题思路

  1. 阶乘函数 (factorial)： 通过递归计算阶乘，并使用数组 factorial_array 进行记忆化，以避免在相同参数上的重复计算。
  2. 排列函数 (permutation)： 通过调用阶乘函数计算排列的总数，该函数返回以输入整数为长度的排列的数量。
  3. 字典序索引计算函数 (dictNum)： 该函数通过模拟字典序生成的过程，计算给定整数序列在字典序中的索引。它使用一个辅助链表 sup_array 来存储部分已经排好序的数字，然后遍历输入数组，计算每个数字在当前序列中的相对位置，从而得到总的字典序索引。
  4. 主函数 (main)：
    • 读取输入文件中的整数 n 和整数数组 data。
    • 调用 dictNum 函数计算字典序索引，并将结果写入输出文件。
    • 尝试找到下一个字典序排列，如果找到，将其写入输出文件。

▲代码

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define rep(i, s, n) for (int i = s; i < n; i++)
#define reb(i, d, n) for (int i = d; i >= n; i--)
const int N = 100;
ll factorial_array[N];
list<int> sup_array; // 辅助数组
ll factorial(int n)
{if (factorial_array[n] != 0)return factorial_array[n];ll res = 1;for (int i = 1; i <= n; i++)res *= i;factorial_array[n] = res; // 记忆，避免重复计算return res;
}
ll permutation(int n)
{ll res = 1;rep(i, 2, n)res *= factorial(i);return res;
}ll dictNum(int *data, int size)
{// 将数字插入辅助数组中，判断有多少个比其小的数int index = 1;ll res = 0;sup_array.push_back(data[0]);res += (data[0] - 1) * factorial(size - 1);for (int i = 1; i < size; i++){list<int>::iterator p = sup_array.begin();int min_nums;int j;for (j = 0; p != sup_array.end(); p++, j++){if (data[i] < *p) // 升序排列 找到位置{min_nums = (data[i] - j - 1);sup_array.insert(p, data[i]);break;}}if (p == sup_array.end()){min_nums = (data[i] - j - 1);sup_array.push_back(data[i]);}res += (min_nums)*factorial(size - i - 1);}return res;
}int main()
{int n;ifstream fin;fin.open("input.txt", ios::in);if (!fin.is_open()){cerr << "input.txt not found" << endl;return -1;}ofstream fout;fout.open("output.txt", ios::out);fin >> n;int data[N];// cout << factorial(7) + 4 * factorial(6) + 2 * factorial(5) + 2 * factorial(4) + 3 * factorial(3) + 1 << endl;rep(i, 0, n){fin >> data[i];}fout << dictNum(data, n) << endl;// 寻找下一个，倒着遍历 直到找到第一个比最后一个小的数，然后交换，再把后面排序即可bool flag = 0;reb(i, n - 2, 0){if (data[i] < data[n - 1]){swap(data[i], data[n - 1]);sort(data + i + 1, data + n);flag = 1;break;}}if (!flag)sort(data, data + n);rep(i, 0, n)fout<< data[i] << " ";fin.close();fout.close();return 0;
}

▲验证

书上验证案例通过。

<4> 算法实现题 2-7 集合划分问题

▲问题重述

n 个元素的集合{1,2,……, n }可以划分为若干个非空子集。例如，当 n=4 时，集合{1，2，3，4}可以划分为 15 个不同的非空子集如下：

{{1}，{2}，{3}，{4}}，
{{1，2}，{3}，{4}}，
{{1，3}，{2}，{4}}，
{{1，4}，{2}，{3}}，
{{2，3}，{1}，{4}}，
{{2，4}，{1}，{3}}，
{{3，4}，{1}，{2}}，
{{1，2}，{3，4}}，
{{1，3}，{2，4}}，
{{1，4}，{2，3}}，
{{1，2，3}，{4}}，
{{1，2，4}，{3}}，
{{1，3，4}，{2}}，
{{2，3，4}，{1}}，
{{1，2，3，4}}

编程任务：
给定正整数 n，计算出 n 个元素的集合{1,2,……, n }可以划分为多少个不同的非空子集。

数据输入：
由文件 input.txt 提供输入数据。文件的第 1 行是元素个数 n。

结果输出:
程序运行结束时，将计算出的不同的非空子集数输出到文件 output.txt 中。

▲解题思路

这道题在实验里做过了，在实验里我给出了三种方法解决这道题，详细可以参考实验报告2。

这里作为作业，为了简单考虑，我采取先求出第二类斯特林数再加和得到贝尔数的方法来解决。

【贝尔数】

B[n]的含义是基数为 n的集合划分成非空集合的划分数。

贝尔数自身递推关系： B[n+1] = ∑ C(n,k) B[k] ，其中k从0到n。

其中定义B[0] = 1

【第二类斯特林数】

第二类斯特林数实际上是集合的一个拆分，表示将 n个不同的元素拆分成m个集合间有序（可以理解为集合上有编号且集合不能为空）的方案数，记为 S(n,m) （这里是大写的）或者 {n m} (n在上m在下) 。

和第一类斯特林数不同的是，这里的集合内部是不考虑次序的，而圆排列圆的内部是有序的。常常用于解决组合数学中的几类放球模型。描述为：将n个不同的球放入m个无差别的盒子中，要求盒子非空，有几种方案。

S(n,k)的值可以递归的表示为：S(n+1, k) = kS(n, k) + S(n, k-1)。

递推边界条件：

S(n,n) = 1, n>=0

S(n,0) = 0, n>=1

为什么会这样表示呢？当我们将第（n + 1）个元素添加到k个划分集合时，有两种可能性。

  • 第n + 1个元素作为一个单独的集合参与到划分成k个集合，有S(n,k-1)个。
  • 将第n + 1个元素添加到已经划分的k个集合中，一共有k*S(n,k)种。

▲代码

#include <bits/stdc++.h>
#include <iostream>
using namespace std;
typedef long long ll;
typedef int itn;
const int N = 5000;
const int mod = 998244353;
int n, m, k;
ll S[N][N];
ll B[N];int solve_S(int n, int k)
{S[0][0] = 1;S[n][0] = 0;for (int i = 1; i <= n; ++i){for (int j = 1; j <= k; ++j){S[i][j] = (S[i - 1][j - 1] + 1ll * j * S[i - 1][j]) % mod; // 公式中的 k 是当前的 k}}return 0;
}ll Bell(int n)
{if (n == 0)return 1;ll ans = 0;for (int k = 0; k <= n; k++){if (!S[n][k])solve_S(n, k);ans += S[n][k];ans = ans % mod;}return ans;
}
int main()
{for (int i = 0; i < N; i++)B[i] = 0;B[0] = 1;int n, T;scanf("%d", &T);for (int i = 0; i < T; i++){scanf("%d", &n);// printf("ans = %lld\n", Bell(n));printf("%lld\n", Bell(n));}return 0;
}

▲验证

洛谷P5748 集合划分计数（https://www.luogu.com.cn/problem/P5748）（与书本问题有细微差异：数据多组，要求取模）

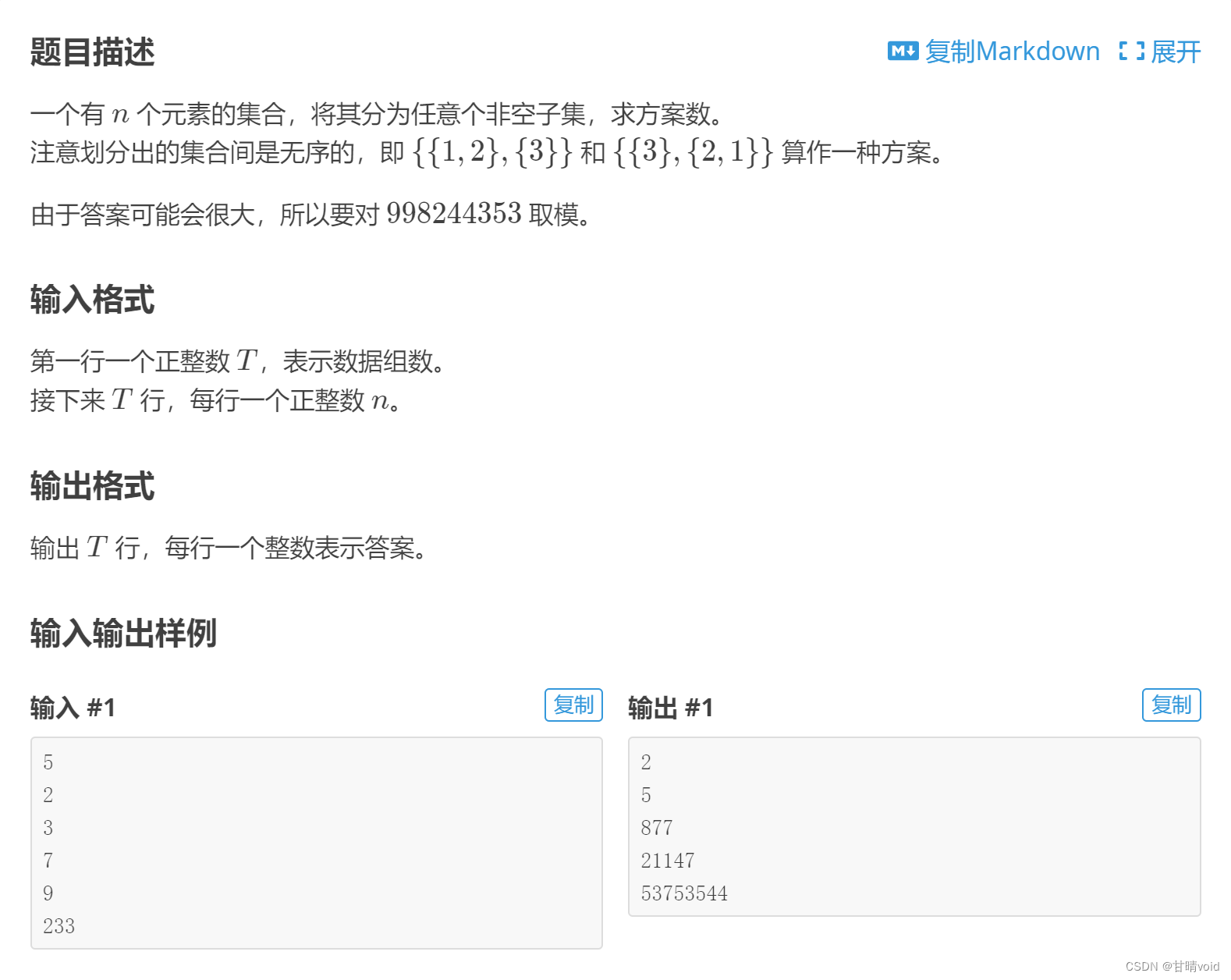
在这里插入图片描述

这篇关于HNU-算法设计与分析-作业2的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/994142。

相关文章

Redis主从复制实现原理分析

Redis主从复制实现原理分析

《Redis主从复制实现原理分析》Redis主从复制通过Sync和CommandPropagate阶段实现数据同步,2.8版本后引入Psync指令,根据复制偏移量进行全量或部分同步,优化了数据传输效率... 目录Redis主DodMIK从复制实现原理实现原理Psync: 2.8版本后总结Redis主从复制实
阅读更多...
锐捷和腾达哪个好? 两个品牌路由器对比分析

锐捷和腾达哪个好? 两个品牌路由器对比分析

《锐捷和腾达哪个好?两个品牌路由器对比分析》在选择路由器时，Tenda和锐捷都是备受关注的品牌，各自有独特的产品特点和市场定位，选择哪个品牌的路由器更合适，实际上取决于你的具体需求和使用场景，我们从... 在选购路由器时，锐捷和腾达都是市场上备受关注的品牌，但它们的定位和特点却有所不同。锐捷更偏向企业级和专
阅读更多...
Spring中Bean有关NullPointerException异常的原因分析

Spring中Bean有关NullPointerException异常的原因分析

《Spring中Bean有关NullPointerException异常的原因分析》在Spring中使用@Autowired注解注入的bean不能在静态上下文中访问,否则会导致NullPointerE... 目录Spring中Bean有关NullPointerException异常的原因问题描述解决方案总结
阅读更多...
python中的与时间相关的模块应用场景分析

python中的与时间相关的模块应用场景分析

《python中的与时间相关的模块应用场景分析》本文介绍了Python中与时间相关的几个重要模块：`time`、`datetime`、`calendar`、`timeit`、`pytz`和`dateu... 目录1. time 模块2. datetime 模块3. calendar 模块4. timeit
阅读更多...
python-nmap实现python利用nmap进行扫描分析

python-nmap实现python利用nmap进行扫描分析

《python-nmap实现python利用nmap进行扫描分析》Nmap是一个非常用的网络/端口扫描工具,如果想将nmap集成进你的工具里,可以使用python-nmap这个python库,它提供了... 目录前言python-nmap的基本使用PortScanner扫描PortScannerAsync异
阅读更多...
Oracle数据库执行计划的查看与分析技巧

Oracle数据库执行计划的查看与分析技巧

《Oracle数据库执行计划的查看与分析技巧》在Oracle数据库中,执行计划能够帮助我们深入了解SQL语句在数据库内部的执行细节,进而优化查询性能、提升系统效率,执行计划是Oracle数据库优化器为... 目录一、什么是执行计划二、查看执行计划的方法（一）使用 EXPLAIN PLAN 命令（二）通过 S
阅读更多...
不懂推荐算法也能设计推荐系统

不懂推荐算法也能设计推荐系统

本文以商业化应用推荐为例，告诉我们不懂推荐算法的产品，也能从产品侧出发， 设计出一款不错的推荐系统。 相信很多新手产品，看到算法二字，多是懵圈的。 什么排序算法、最短路径等都是相对传统的算法（注：传统是指科班出身的产品都会接触过）。但对于推荐算法，多数产品对着网上搜到的资源，都会无从下手。特别当某些推荐算法 和 “AI”扯上关系后，更是加大了理解的难度。 但，不了解推荐算法，就无法做推荐系
阅读更多...
作业提交过程之HDFSMapReduce

作业提交过程之HDFSMapReduce

作业提交全过程详解 （1）作业提交 第1步：Client调用job.waitForCompletion方法，向整个集群提交MapReduce作业。 第2步：Client向RM申请一个作业id。 第3步：RM给Client返回该job资源的提交路径和作业id。 第4步：Client提交jar包、切片信息和配置文件到指定的资源提交路径。 第5步：Client提交完资源后，向RM申请运行MrAp
阅读更多...
康拓展开（hash算法中会用到）

康拓展开（hash算法中会用到）

康拓展开是一个全排列到一个自然数的双射（也就是某个全排列与某个自然数一一对应） 公式： X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0! 其中,a[i]为整数,并且0<=a[i]<i,1<=i<=n。（a[i]在不同应用中的含义不同）； 典型应用： 计算当前排列在所有由小到大全排列中的顺序，也就是说求当前排列是第
阅读更多...
性能分析之MySQL索引实战案例

性能分析之MySQL索引实战案例

文章目录 一、前言二、准备三、MySQL索引优化四、MySQL 索引知识回顾五、总结 一、前言 在上一讲性能工具之 JProfiler 简单登录案例分析实战中已经发现SQL没有建立索引问题，本文将一起从代码层去分析为什么没有建立索引？ 开源ERP项目地址：https://gitee.com/jishenghua/JSH_ERP 二、准备 打开IDEA找到登录请求资源路径位置
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2