本文主要是介绍考研数学|李林《880》做不动,怎么办!?看这一篇!,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在考研数学的备考过程中,遇到难题是很常见的情况,尤其是当你尝试解决李林880习题集中的问题时。他以其难度和深度著称,旨在帮助考生深入理解数学分析的复杂概念。
如果你在解题过程中感到困难,这并不是你个人的问题,而是大多数考生在备考过程中都会遇到的挑战。以下是一些建议,希望能帮助你更有效地应对这些难题。
首先数学分析的核心在于对极限、连续性、微分和积分等概念的深入理解。确保你对这些概念有清晰的理解,因为它们是解决更复杂问题的基础。
不要急于求成,可以先从简单的题目开始,逐步提高难度。逐步建立你的解题能力,这有助于增强你的信心。
在遇到难题时,可以查阅相关的教材、参考书或网络资源,了解不同的解题思路。有时候,不同的解释或方法会帮助你打开思路。
另外,数学学习是一个长期的过程,需要耐心和毅力。同时需要不断复习来巩固记忆。定期回顾已学过的知识点,有助于加深理解。记住不要因为一时的困难而气馁哦!
为了能长久地坚持,也要保持积极乐观的心态,相信自己能够逐步克服困难。心态的调整对于学习效率至关重要。为自己设定短期和长期的学习目标,这也有助于保持动力和方向。
最后,记住!每个人的学习节奏和方式都是不同的,找到适合自己的方法是关键。不要因为暂时的困难而放弃,坚持不懈,你会逐渐提高解题能力,最终克服这些难题。
接下来,我将仔细回顾我第一次和第二次考研的经历,特别是我所遇到的问题和踩过的坑。希望这些经验能对大家有所帮助。
二战回顾
考研成败很大程度上取决于数学,得数学则上岸!!!
考研过程犹如马拉松,其中除了坚韧的意志外,最重要是避免走冤枉路!
一战时,我尝试了不同老师的课程,拿起题目却毫无头绪,不断地看课,却未及时开始动手做题。当我意识到做题的重要性时,时间已经不足。
我觉得我自己就是考研数学复习的大多数——一战结束时不得不接受考试现实,真实而残酷。
一战的教训
在一战落败后的深刻反省中,我认识到了一个核心问题:缺乏足够的动手解题能力。
俗语有云:“眼见未必为实”。对于习题而言,就是这样的情况。你可能碰到一个不会解的题目,直觉上会去查找答案并误以为自己理解了,然而实际上,你仅仅是记下了答案,并没有真正的理解。
正因为此,我强烈建议所有的同学重视结合“做题+培养计算能力” " 这个重点。
但是,盲目的题海战术并不是提升数学成绩的最佳路径,应该有针对性地做题才能提高对知识点的掌握能力。
对我来说,在二战中,我决定从题目出发,重新学习并吸收各个知识点。我选用了一个名为「知能行考研数学」的刷题平台。
知能行考研数学知能行考研数学通过大数据分析历年真题的考点难点,为每位考生选择快速提高的突破口。知能行基于机器学习追踪考生知识点的掌握情况,测练合一从而达到高效备考![]() https://bestzixue.com/?app_referrer_id=DXW~atczc-l8-0511-editor_jnx
https://bestzixue.com/?app_referrer_id=DXW~atczc-l8-0511-editor_jnx

我二战全程使用了这个平台,因为知能行能够让我有针对性地做题,在每一个层级上扎实地构建基础。简单概括就是将知识点拆分为易于消化的小单元,从而构筑起一个全面且无死角的知识体系。
平衡看课和做题
在数学的学习和复习阶段,平衡观看课程和做题练习是至关重要的。
我一战就是一味看视频,不进行做题输出,到了后期才去做题,才发现会出大问题 …
仅靠观看视频学习常会遇到这样的问题:看完视频,甚至做了笔记,但是当问起其中内容便一筹莫展。
但如果直接做题又会有一种两眼一抹黑的情况发生,这样非常不利于我们对于自己做题的主动性。
在利用知能行学习平台时,每章节伊始,都会附带一个「复习要点」,这其中罗列了关键的知识框架。
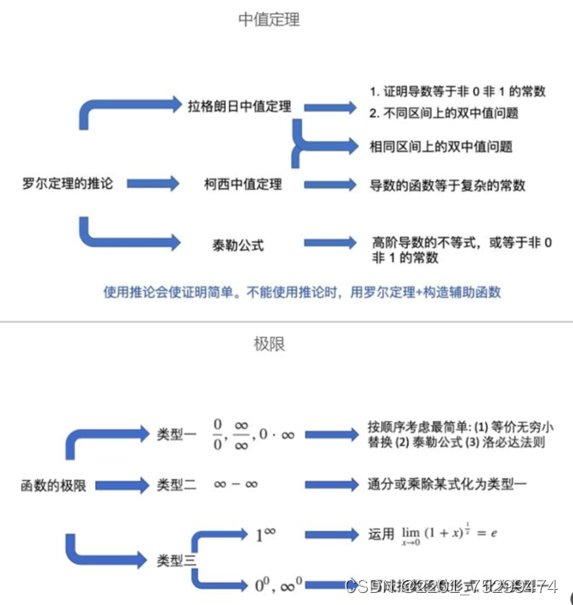
在听课时,经常会发生听完一节课,但“脑袋空空”的情况。在这种情况下,我们可以在看视频前,通过知识点列表来设立明确的学习目标,以提升学习效率。
尤其是要善于运用知能行的知识点拆分功能。我们需要先了解章节涵盖哪些知识点,随后带着对这些点的疑问观看视频里的老师是如何阐释、推导出结论的。
采用这种方法,我们可以避免看完视频后仍然一无所获的情况。
观看完视频课程后,就可以使用知能行对应章节进行实操练习,通过做题来巩固知识、测试理解水平。这不仅加强了对之前学习内容的记忆,而且有助于及时补充知识点的遗漏。
采纳交替进行看视频和做题的学习方法,既确保在学习过程中我们能够吸收新知识,又能够在适时巩固和应用所学的知识和技能。
有目标的规划
一开始每当我遇到不会的题,就去翻答案,去背答案。我逐渐意识到,这样的方法只是表面掌握了问题的解决方法,没有真正理解这类型问题的核心逻辑。
而投入更多的时间钻研题目的基本原理,从长远来看,为后期的学习节省了宝贵时间。
备考考研是个持久作战,整整一年的时间里,会不断耗费大量时间与精力。许多人因缺乏明确目标而随波逐流。
最糟糕的情况就是一直不检验自己的复习效果,到了后期才发现复习出了大问题。
在我的二战过程中,我开始运用知能行作为工具,它的强大功能实在出乎我的预料。首要的是,知能行利用人工智能技术和大数据分析,结合我的学习数据提出个性化的学习方案。
这个平台可以针对我的需求提供合理的学习计划,安排课程和复习时间段,极大提升了我管理时间的效率。

这一点知能行的全程规划中也有说到,我们可以在刷完知能行相应的章节等级之后去用习题册对自己的学习成果进行一个检验。
譬如,在基础阶段使用1800基础篇,在强化阶段使用660、880等,到了冲刺阶段则可以借助模拟卷和真题来检验能力。基本上在刷完知能行之后,1800、660等习题册的一刷正确率可以达到80%以上
还有更细致的安排在全程计划的详细计划里和知能行的小目标里都有,可以看到你应该去刷相应的习题册里具体的哪些题目。

每个学习阶段又细分为多项任务,我们可以利用这些指引更好地筹划自己的复习计划。因为知能行提供的训练方案个性化强,所以每个人的进度都是独一无二的,需要根据个人实际情况进行调整。
总而言之,实际训练时间取决于个人基础水平。基础扎实的话,训练时间相对较短;基础薄弱则要付出更多时间。
在我的学习经历中,对积分章节的理解和掌握速度比较慢,曾感到相当焦虑。但在学完相应内容并着手660题目时,就发现努力都不是白费哒!
计算能力的训练
一战直到后期,我才意识到自己做题不熟练,计算不稳定的问题,可惜为时已晚,犯了一种看到题目知道解法,但答案算不对的毛病 😭
在训练计算能力时,我们内心往往对那些涉及繁琐计算的题目感到厌恶。在解决传统题目过程中,一旦我们计算出错,大多只是匆匆查看答案与过程,随即进入下一题。
半途而废的放弃,对难题的畏惧,以及连简单题目都出错,这正是"眼高手低"的问题所在。这个坏习惯在一战中让我吃了大亏。
实际上,遭遇难题和大量计算是很常见的,例如需要综合多个基本初等函数复合(如反函数、指数、三角等),还可能会涉及乘方、开方、高阶导数,甚至是阶乘和无限序列等元素,这些都是正常的难度。
考研数学中的计算量非常庞大,可能需要分类讨论,可能融合众多知识点,甚至可能包含高层次的模型背景。计算是基础技能,如果连基本计算都错误,解决证明类问题更是无从谈起。有时候,灵活运用计算技巧也显得至关重要。
计算一错,全盘皆输! 计算能力考验个人的细心和基础功底,所以在复习初期,我们就要踏踏实实地练习计算和常规解题方法。如果做不动题目,通常是因为计算方法不熟练和畏难情绪导致的。
计算不行解决计算,情绪不行解决情绪,没有捷径可走。
培养举一反三,灵活变通的能力
一战的时候我虽然能够掌握书上的例题,但一遇到课后习题册上的题目,我就开始束手无策了。
就以备考时要刷习题册为例,虽然二刷和三刷是一种好的方法,但问题是如何合理统筹一刷、二刷和三刷的关系,这是大多数人处理不好的问题。
同类型的题目,换个数据、题干变化一点点,就不能立刻联想到考点和具体解法。也不能根据题目的条件选择最合适的方法
这里需要强调的是,平时做题从来没有按题型总结常规解法,培养灵活变通的能力,正如汤家凤老师的表情包所示:"我有千万种解题思路,而你却无可奈何"。
知能行推荐了一种非常有效的练习策略,就是当你对一道理应解得出的题目感到困惑时,它会点拨你回想之前解决过的类似题目,以此来实现举一反三,提高解题效率。

通过这种方式,解决了我之前一看题目就无从下手。我开始有意识地将掌握的知识点与解决问题的方法联系起来。
下面,我将详细介绍各个复习阶段的策略以及应留心的要点。
基础阶段
考研数学基础阶段至关重要,这阶段决定了你在基础题目上的得分能力。
在基础阶段,关键在于全面审视每一个知识点。有效进行这一“扫描”的途径,往往是通过观看知识点讲解视频。
平衡视频学习和实际做题
观看教学视频时,要专注于深刻理解和吸收知识。
有时纯粹观看视频并不能确保知识的内化,反而可能在看完后不知所获。但如果直接做题又会有一种两眼一抹黑的情况发生,这样非常不利于我们对于自己做题的主动性。
所以我觉得看视频和做题之间应该是相辅相成的关系。
听课却解不出题就是白听,复习效果=0
首先知能行每章都有免费的突破口,这对于看完课程视频之后不知道自己掌握如何的我非常贴心。
在做题的过程中如果遇到了一些困难,有些题反反复复总是做不会,可以再去找相关的知识点的视频,去看看各位老师在遇到这类题目时应该往哪些方面去思考。
或者可以看看是否在遇到这类题时有一些小技巧帮助思考。
如果某一章掌握的不错的话,那很快就能在知能行达成一级满级了。如果满级了知能行不让继续做了,也要记得在接下来好好做综测哦;
掌握的不好也没关系,知能行会通过AI技术分解扫描基础,找出最底层的薄弱点并带着我解决这些问题,而不仅仅是只把当前做的这道题学会。
只有这样才能把基础打好,不会只是“虚假”地学会了某道题,而是学会了一类题。看似用了更多的时间学某一题,其实为之后的学习省去了许多时间。
那么到这里基础阶段就结束了吗?NONONO,并没有完。这一点知能行的全程规划中也有说到,我们可以在刷完知能行相应的章节等级之后去用习题册对自己的学习成果进行一个检验。
滚动复习,对抗遗忘
知能行的“跨专题综合测试”功能尤为实用,它基于AI对你在平台上做过的所有题目进行系统性评估,并提供复习建议以及循环复习那些曾答错或掌握不牢的题目。
这种方式类似数学版的艾宾浩斯遗忘曲线,可以将综合测验看作是切中复习软肋的模拟测试。
综合测验的目的是为了检验知识掌握程度,及时补充弱项,确保考试全面准备。
此外,综合测验的经历有助于熟悉真实考试环境和难度,优化时间管理,提升应试技能。其结果同时可助于调整复习方向,集中力量攻克关键问题。
通过综测的结果,我们可以清晰看到自己的进步,并因此增强信心,为未来学习奠定坚实基础。
每次综测正确率高,就能发现进度条猛猛涨!自信和满足upupup!
强化阶段
基础阶段结束后,就进入考研数学中最折磨大脑的强化阶段了,大家通常在暑假前后进入这个阶段。到了强化阶段,大家会发现自己面临的题目难度急剧提高,无论是讲义上的例题、课后习题,还是习题册上的题目,难度都较高。
进入强化阶段之际,我就没有再去看什么强化视频了,仅针对性地观看一些能提供实用技巧的考研数学视频。
在此阶段,我主要是在知能行平台上进行深入学习和实践。基本上就是在知能行“摸爬滚打”(bushi)。首先呢,要先确保每一章都把一级刷满级,这样才能往下走。
然后,在知能行,最最重要的就是综测。通过分析综测结果,我们可以清晰地了解自己在哪些知识点上存在不足。从而有针对性地制定学习计划,重点突破弱项,有利于提高整体数学水平。
当综测中出现错误时,噔噔!小黄点!你错的题目在哪一章节,就会发现切换章节的页面中那章后面出现了小黄点。出现小黄点该怎么办?消灭它!!
对付小黄点的重要性并不亚于综测本身。把综测比作是定位隐藏敌人,而消除小黄点则是直接与之交战。知道了敌人所在,不打败他你睡得着觉吗!

除此之外,和基础阶段一样。除了知能行,我们也可以通过660、880等习题册来检验自己的学习成果。
对于这一点,知能行有一个很妙的功能,它会通过平时做题的正确率猜测我在这些习题册中的掌握情况,帮助我提高效率。
“660AI猜你会”会将每一道题都划分到三个不同的档次:能力尚未达标、也许可以、相信自己是可以的!分别是红、橙、绿色的标志。

对绿色标记的题目,简略审视即可,如有思路则可以跳过节约时间;橙色的题目建议尽量尝试解答,解答完成后,不论对错,均需将结果输入知能行,以便平台更准确评估你的实际水平;至于红色标记题目,如无头绪,先针对相关章节在知能行上加强训练,待下次再挑战。
冲刺阶段
随着考试的临近,冲刺阶段的重要性不言而喻。先得提一嘴,这一阶段心态和情绪的管理比平时更加关键,因为只有心态好,学习效率才会更高。
这个时候知能行也贴心地推出了冲刺模式,我来介绍一下冲刺模式有些什么新东西呢。
12月24日能力条,它可以预测你在考试那天对于这一章做题的能力,在这个阶段,等级4、5也会随之消失。是因为等级4、5是对于长期能力的锻炼,而在冲刺阶段,更重要的是优化长期能力与短期记忆的比例。
另外这个阶段依然不能放弃综测,综测会将之前所有的知识点再全部过一遍。同时,通过综测的反馈,我们也可以更清楚地认识到自己的进步,从而增强信心,缓解临近考试的紧张感。
同时,综测的作用依旧不可小觑,在这个时间段,它会帮助我们复习前面学过的所有知识点。综测反馈也助于我们定位自身的提升,并通过明显的进步来增强信心,缓解考前焦虑。
此外,还会提供综测计划,为每天应进行的综测数量制定计划。但这个计划会根据你的综测正确率和之前的综测完成量作出相应的调整。
至于是否需要做真题,有可能知能行已经帮你解决了这个问题。在冲刺阶段,有一个“真题预测”功能,它能够预估你在近10年真题中的得分。
类似于之前的660预测,它会把每道题目分类为:能力尚未达标、可能掌握、有信心做对。属于前两档的题目也不用担心,它会贴心地告诉你该去哪里进行练习哒!
几点建议
考研数学考的就是计算能力
考研数学的考试中计算量非常大(这几年考完就上热搜),这不仅检验考生是否具有扎实的数学基础,也测试考生在面临挑战时的心理承受能力。
基础功这点,知能行会筛选数一、二、三的知识点,只要在大纲内,数二、数三的题会拿来给数一练习,数一、数三的题也会拿来给数二练习,这样基础就全面了。
而且题量也够大,每天的综测更是能一直锻炼大家的心态(我第一次碰到综测爆炸的时候心态也一起爆炸了),让大家到了考场上无论遇到什么情况,心态炸不了一点。
从我个人经验来看,知能行在提供计算量训练及针对性刷题方面做得极好。
保持手感
坚持每日做题对保持数学手感尤为重要。中断练习会导致考试时手感消失,易引起紧张。
知能行提供的综测可以帮助你在复习错题和尝试新题之间找到平衡。有多余时间时,也可以尝试张宇的6+4模拟卷来练习。
重视错题
在追求学习进度时切勿忽视错题的重要性。特别是在复习后期,不重视错题可能会丧失提升成绩的机会。
不要迷信押题
任何考试均存在押题现象,众所周知,押题本质上是场概率游戏。押中虽好,但未押中的可能性更大。
与其把钱和精力用在概率事件上,不如扩大自己的复习覆盖率,当然完全依靠押题的话大概率是因为也没有足够的时间了。在这种情况下我建议可以使用知能行的保命模式,他可以帮助你在跳过一些题目时做到有的放矢。
最后,请相信你为了达到目标所付出的努力终将有价值。
生活充满惊喜,只要你努力付出,命运终将给予满意的回报。
持之以恒,终将成功,顺利上岸!
这篇关于考研数学|李林《880》做不动,怎么办!?看这一篇!的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







