强化训练：day8（求最小公倍数、数组中的最⻓连续⼦序列、字⺟收集）

本文主要是介绍强化训练：day8（求最小公倍数、数组中的最⻓连续⼦序列、字⺟收集），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

  1. 最小公倍数
  2. 数组中的最⻓连续⼦序列
  3. 字⺟收集

1. 最小公倍数

1.1 题目描述

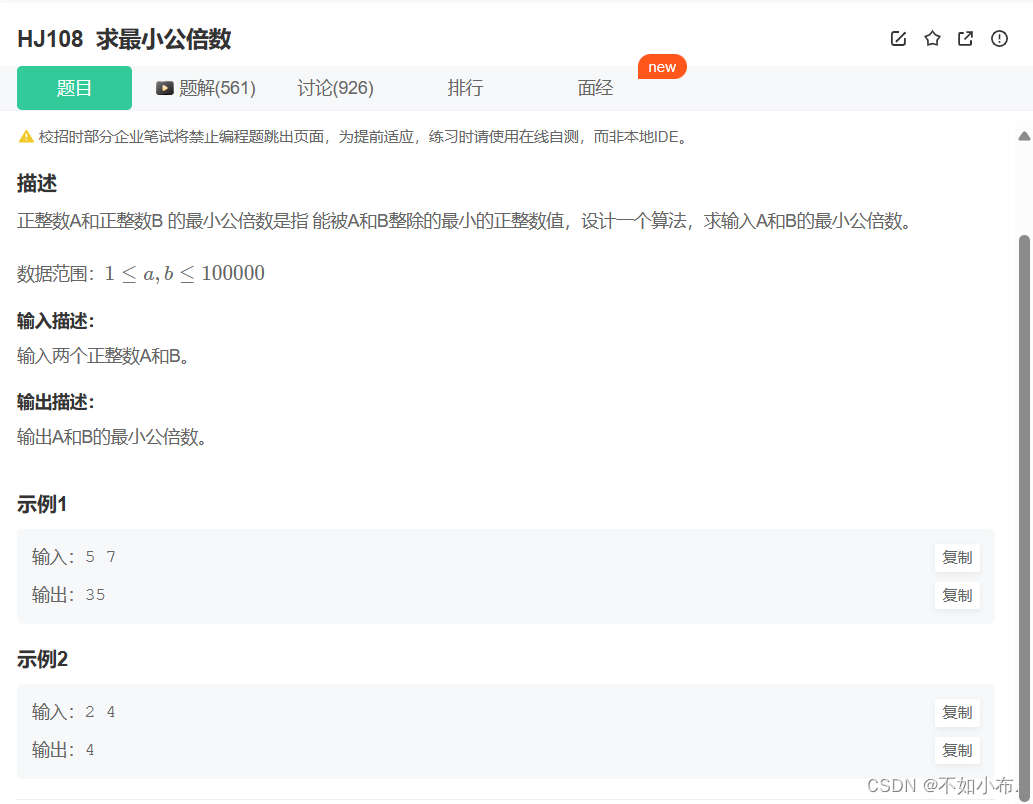
1.2 解题思路

  最小公倍数= A * B / 最大公约数（数学中的短除法），最大公约数：辗转相除法。

1.3 代码实现

#include <iostream>
using namespace std;
using ll = long long;
// 求最大公约数 -> 辗转相除法
ll solve(ll x, ll y) 
{ll ret = 0;while (x % y != 0) {ret = x % y;x = y;y = ret;}return y;
}
int main() 
{ll x, y;cin >> x >> y;ll num = solve(max(x, y), min(x, y));// 短除法ll ret = (x / num) * (y / num) * num;cout << ret;return 0;
}

2. 数组中的最⻓连续⼦序列

2.1 题目描述

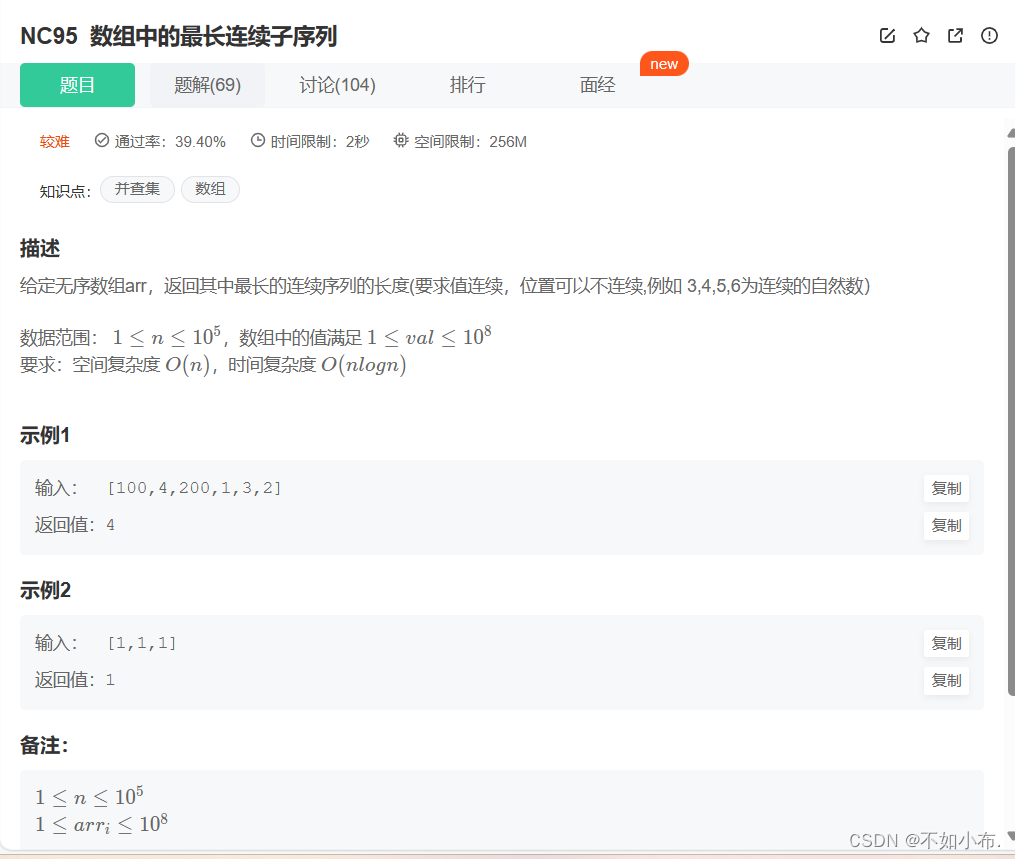
2.2 解题思路

  排序 + 模拟，我们要找的是最长的连续子序列，题目明确说了，只要求值连续，不要求位置连续，因此可以进行排序来帮助我们进行解题。
  排序之后就是从小到大排列，那么问题就简单，我们一次枚举一遍，看看当前值和前一个值的大小是不是相差为1即可，符合条件就将我们的计算count++，不符合就从当前位置开始下一次的判断。不过需要注意的是重复数字的问题，因为对于重复数字还需要进行判断，只需要将我们的标记指针向后移动，计算count不变就可以了。
  我一开始就没有考虑到重复数字的问题，导致没写出来……

2.3 代码实现

class Solution {public:// 注意处理数据重复的问题！！！！！！！using ll = long long;int MLS(vector<int>& arr) {int n = arr.size();sort(arr.begin(), arr.end());int left = 0;int len = 0;while (left < n) {int right = left + 1;int count = 1;while(right < n){if(arr[right] - arr[right - 1] == 1) {right++;count++;}else if(arr[right] - arr[right - 1] == 0){right++;}else{break;}}len = max(len, count);left = right;}return len;}
};

3. 字母收集

3.1 题目描述

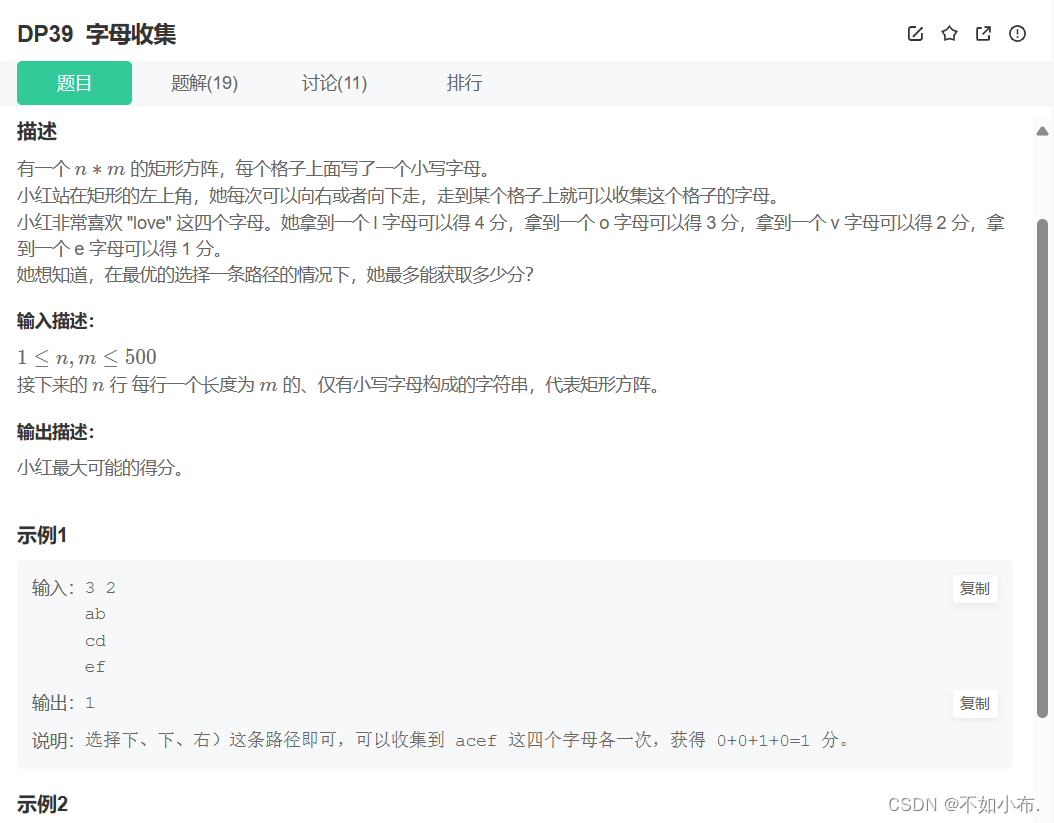
3.2 解题思路

  简单的路径dp问题，我们可以根据题目描述来设置状态，设置一个二维的dp数组，dp[i][j]表示到达 [ i ，j ] 位置最多能获得多少分。而每一个位置的分数与两个位置有关，那就是二维数组中当前位置的上方的数据和左边的数据。
  那么状态转移方程就是：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + add(grid[i - 1][j - 1])； 继续来解释一下，先说add函数，它是用来表示 i，j 位置的字符所得的分数，至于为什么要减1，一会说。我们现在知道了当前位置所能获得的最大分数来自于两个方向，我们肯定需要取大的一个，所以用max，取到大的分数之后，还需要加上当前位置的字母的分数，才是到达当前位置所能获得的最大分数。
  至于为什么减1，则是因为，我们来第一个位置的，它需要它的上面的和左边的数据，但是这是会越界的，所以我们可以将dp表多开一行一列，来避免越界问题。比如，字母的位置是0 0（也就是第一个字符），那么它在dp表中的位置就是1 1，这样就可以避免越界问题了。但是在统计字符分数，就需要进行减一来找到原来的位置了。（不理解的可以画一个二维数组来看一下）

3.3 代码实现

#include <iostream>
using namespace std;
#include <vector>
#include <string>
#include <cstring>
int m, n;
int add(char s) 
{if (s == 'l') return 4;else if (s == 'o') return 3;else if (s == 'v') return 2;else if (s == 'e') return 1;else return 0;
}
int main() 
{cin >> m >> n;vector<vector<char>> grid(m, vector<char>(n));vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));   for (int i = 0; i < m; i++)for(int j = 0; j < n; j++)cin >> grid[i][j];for (int i = 1; i <= m; i++)for (int j = 1; j <= n; j++) {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + add(grid[i - 1][j - 1]);}cout << dp[m][n];    return 0;
}

总结

  处理第一题，后面两个题还是有很多细节的地方要处理的，而且对于这种题，看题解可能一看就会了，一写就废了，原因就是有很多的边界问题以及条件判断并没有搞清楚或者说没有意识到，所以总是出错。而为了能避免这种情况，只能是多写，不能光看不写。
  那么第八天的内容就到此结束了，如果大家发现有什么错误的地方，可以私信或者评论区指出喔。我会继续坚持训练的，希望能与大家共同进步！！！那么本期就到此结束，让我们下期再见！！觉得不错可以点个赞以示鼓励！

这篇关于强化训练：day8（求最小公倍数、数组中的最⻓连续⼦序列、字⺟收集）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---