本文主要是介绍IB 公式解析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
公式
3.2. Influence Function
影响函数允许我们在移除样本时估计模型参数的变化,而无需实际移除数据并重新训练模型。

3.3 影响平衡加权因子
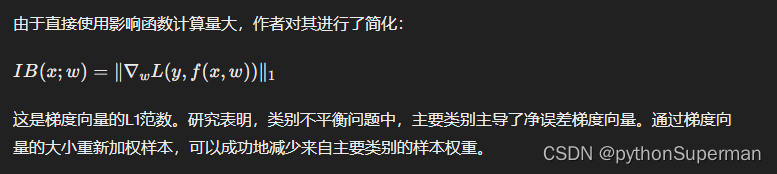
3.4 影响平衡损失


3.5 类内重加权

m代表一个批次(batch)的大小,这意味着公式对一个批次中的所有样本进行计算,然后去平均值。

代码
criterion_ib = IBLoss(weight=per_cls_weights, alpha=1000).cuda()def ib_loss(input_values, ib):"""Computes the focal loss"""loss = input_values * ibreturn loss.mean()class IBLoss(nn.Module):def __init__(self, weight=None, alpha=10000.):super(IBLoss, self).__init__()assert alpha > 0self.alpha = alphaself.epsilon = 0.001self.weight = weightdef forward(self, input, target, features):grads = torch.sum(torch.abs(F.softmax(input, dim=1) - F.one_hot(target, num_classes)),1) # N * 1ib = grads * features.reshape(-1)ib = self.alpha / (ib + self.epsilon)return ib_loss(F.cross_entropy(input, target, reduction='none', weight=self.weight), ib)
1.计算梯度 grads:
grads = torch.sum(torch.abs(F.softmax(input, dim=1) - F.one_hot(target, num_classes)), 1) # N * 1
- 计算 softmax 概率分布:
F.softmax(input, dim=1)将模型的输出转换为概率分布。 - 计算 one-hot 编码:
F.one_hot(target, num_classes)将目标标签转换为 one-hot 编码。 - 计算绝对差值:通过计算 softmax 输出与 one-hot 编码之间的绝对差值,得到每个样本的梯度,表示样本对模型的损失贡献。

2. 计算影响平衡因子(IB Factor)
ib = grads * features.reshape(-1)
ib = self.alpha / (ib + self.epsilon)
影响平衡因子(IB Factor)确实与梯度成反比。梯度越大,IB因子越小,分配给该样本的权重越小;梯度越小,IB因子越大,分配给该样本的权重越大。这一机制确保了模型在处理不平衡数据时,能够更有效地减小对多数类样本的过拟合,提升对少数类样本的泛化能力。
3. 计算最终损失
return ib_loss(F.cross_entropy(input, target, reduction='none', weight=self.weight), ib)
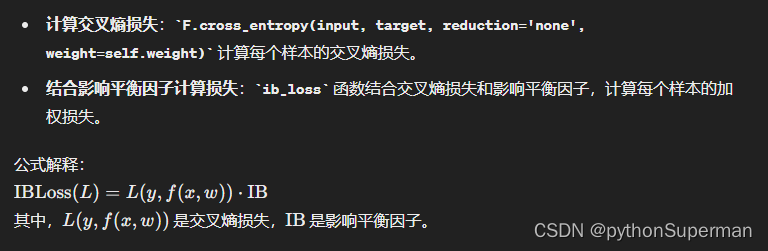
将论文中的公式与代码对应起来
论文中的公式:

对应代码
首先,我们来看影响平衡损失 IBLoss 的代码实现:
class IBLoss(nn.Module):def __init__(self, weight=None, alpha=10000.):super(IBLoss, self).__init__()assert alpha > 0self.alpha = alphaself.epsilon = 0.001self.weight = weightdef forward(self, input, target, features):grads = torch.sum(torch.abs(F.softmax(input, dim=1) - F.one_hot(target, num_classes)), 1) # N * 1ib = grads * features.reshape(-1)ib = self.alpha / (ib + self.epsilon)return ib_loss(F.cross_entropy(input, target, reduction='none', weight=self.weight), ib)
对应关系
-
批次大小 m
在代码中,批次大小由
train_loader或test_loader的批次大小参数决定。 -
数据集 𝐷𝑚
代码中的
train_loader或test_loader提供了批次数据。 -
类别权重因子 𝜆𝑘
在代码中,通过
per_cls_weights来实现:
per_cls_weights = 1.0 / np.array(cls_num_list)
per_cls_weights = per_cls_weights / np.sum(per_cls_weights) * len(cls_num_list)
per_cls_weights = torch.FloatTensor(per_cls_weights).cuda()
4.基本损失函数 𝐿(𝑦,𝑓(𝑥,𝑤))
代码中使用 torch.nn.CrossEntropyLoss 计算交叉熵损失:
base_loss = F.cross_entropy(input, target, reduction='none', weight=self.weight)
5.模型输出 𝑓(𝑥,𝑤)f(x,w)
在代码中,模型的输出为 input:
output, features = model(images)
6.模型输出与真实标签的 L1 范数 ∥𝑓(𝑥,𝑤)−𝑦∥1
在代码中,通过以下方式计算:
grads = torch.sum(torch.abs(F.softmax(input, dim=1) - F.one_hot(target, num_classes)), 1) # N * 1
7.隐藏层特征向量 ℎ 和其 L1 范数 ∥ℎ∥1**
在代码中,通过以下方式计算隐藏层特征向量的 L1 范数:
features = torch.sum(torch.abs(feats), 1).reshape(-1, 1)
8.最终影响平衡因子 IB
在代码中,通过以下方式计算:
ib = grads * features.reshape(-1)
ib = self.alpha / (ib + self.epsilon)
9.最终影响平衡损失 𝐿IB(𝑤)
通过自定义的 ib_loss 函数计算:
return ib_loss(F.cross_entropy(input, target, reduction='none', weight=self.weight), ib)

为什么类别权重因子要这样实现
per_cls_weights = 1.0 / np.array(cls_num_list)
per_cls_weights = per_cls_weights / np.sum(per_cls_weights) * len(cls_num_list)
per_cls_weights = torch.FloatTensor(per_cls_weights).cuda()类别权重因子的实现旨在通过加权样本来处理类别不平衡问题。以下是详细解释为什么要这样实现 per_cls_weights 以及每一步的作用:
代码实现
per_cls_weights = 1.0 / np.array(cls_num_list)
per_cls_weights = per_cls_weights / np.sum(per_cls_weights) * len(cls_num_list)
per_cls_weights = torch.FloatTensor(per_cls_weights).cuda()
每一步的解释
计算每个类别的逆频率:
per_cls_weights = 1.0 / np.array(cls_num_list)
cls_num_list是每个类别的样本数量列表。例如,如果有三个类别,且每个类别的样本数量为[100, 200, 50],则cls_num_list = [100, 200, 50]。- 通过取倒数
1.0 / np.array(cls_num_list),我们得到了每个类别的逆频率。例如,结果将是[0.01, 0.005, 0.02]。 - 逆频率反映了类别数量的稀少程度,样本数量少的类别(少数类)将得到更高的权重。
归一化权重:
per_cls_weights = per_cls_weights / np.sum(per_cls_weights) * len(cls_num_list)
- 首先,计算权重的总和
np.sum(per_cls_weights)。根据前面的例子,总和为0.01 + 0.005 + 0.02 = 0.035。 - 然后,将每个类别的权重除以总和,使得所有权重的和为 1。这是标准化步骤,使得权重变为
[0.01/0.035, 0.005/0.035, 0.02/0.035],即[0.2857, 0.1429, 0.5714]。 - 接下来,将这些标准化权重乘以类别的数量
len(cls_num_list)。在这个例子中,类别数量是 3。因此,最终的权重变为[0.2857*3, 0.1429*3, 0.5714*3],即[0.8571, 0.4286, 1.7143]。
这一步的作用是确保每个类别的权重和类别数量成正比,同时保持权重的总和为类别数量。
转换为 PyTorch 张量:
per_cls_weights = torch.FloatTensor(per_cls_weights).cuda()
- 将 NumPy 数组转换为 PyTorch 张量,以便在 PyTorch 中使用这些权重。
- 将权重张量移动到 GPU(如果可用),以加速计算。
归一化步骤的原因
归一化权重的目的是确保类别权重的相对比例合理,并且所有权重的总和与类别数量一致。这有助于避免某些类别被赋予过高或过低的权重,从而确保训练过程中的稳定性和效果。
处理类别不平衡的原因
类别不平衡问题是指在数据集中,不同类别的样本数量差异很大。在这种情况下,传统的损失函数往往会被多数类主导,导致模型在少数类上的性能较差。通过加权样本,特别是对少数类样本赋予更高的权重,可以平衡各类样本对损失的贡献,从而改善模型在少数类上的表现。
总结
- 逆频率权重:通过取样本数量的倒数,使得样本数量少的类别得到更高的权重。
- 归一化:将权重标准化,并确保权重的总和与类别数量一致,保持权重比例的合理性。
- 转换为张量:将权重转换为 PyTorch 张量,以便在训练过程中使用。
这种权重计算方法确保了在处理类别不平衡问题时,少数类样本对损失函数的贡献增加,从而提高模型对少数类的识别能力。
这篇关于IB 公式解析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






