本文主要是介绍PQ(product quantization) 算法---(一),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
转自:http://vividfree.github.io/
1. 引言
Product quantization,国内有人直译为乘积量化,这里的乘积是指笛卡尔积(Cartesian product),意思是指把原来的向量空间分解为若干个低维向量空间的笛卡尔积,并对分解得到的低维向量空间分别做量化(quantization)。这样每个向量就能由多个低维空间的量化code组合表示。为简洁描述起见,下文用PQ作为product quantization的简称。
The idea is to decomposes the space into a Cartesian product of low dimensional subspaces and to quantize each subspace separately. A vector is represented by a short code composed of its subspace quantization indices.
2011年,Herve Jegou等学者在PAMI上发表了PQ方法的第一篇正式paper[1],用于解决相似搜索问题(similarity search)或者也可以说是近邻搜索(nearest neighbor search)问题。其实这几位作者在2009年的INRIA(即法国国家信息与自动化研究所)的技术报告上已经发表PQ方法。这里插一段题外话,[1]的一作Herve Jegou和二作Matthijs Douze均在2015年跳槽去了Facebook AI research,并在今年3月份合作开源了Faiss相似搜索工具[4]。
近几年,深度学习技术被广泛用于图像识别、语音识别、自然语言处理等领域,能够把每个实体(图像、语音、文本)转换为对应的embedding向量。一般来说,相似的实体转换得到的embedding向量也是相似的。对于相似搜索问题,最简单的想法是暴力穷举法,如果全部实体的个数是n,n是千万量级甚至是上亿的规模,每个实体对应的向量是D,那么当要从这个实体集合中寻找某个实体的相似实体,暴力穷举的计算复杂度是O(n×D),这是一个非常大的计算量,该方法显然不可取。所以对大数据量下高维度数据的相似搜索场景,我们就需要一些高效的相似搜索技术,而PQ就是其中一类方法。
PQ是一种量化(quantization)方法,本质上是数据的一种压缩表达方法(其实通信学科的一个主要研究工作就是研究信号的压缩表达),所以该方法除了可以用在相似搜索外,还可以用于模型压缩,特别是深度神经网络的模型压缩上。由于相似搜索不仅要考虑如何量化的问题,还要考虑如何检索(search)的问题,而模型压缩可能更主要的是考虑如何量化的问题,不用太关注如何检索这个问题,所以这篇文章会主要站在相似搜索上的应用来介绍PQ方法。至于模型压缩,可以找找近几年研究神经网络模型压缩的paper或者一些互联网公司(比如百度, Snap等)发出的一些资料[3]。
2. 相似搜索的若干种方法
参考文献[5][6]很好的总结了相似搜索的几类方法,这里简要总结几个核心点。可以将方法分为三大类:
- 基于树的方法
- KD树是其下的经典算法。一般而言,在空间维度比较低时,KD树的查找性能还是比较高效的;但当空间维度较高时,该方法会退化为暴力枚举,性能较差,这时一般会采用下面的哈希方法或者矢量量化方法。
- 哈希方法
- LSH(Locality-Sensitive Hashing)是其下的代表算法。文献[7]是一篇非常好的LSH入门资料。
- 对于小数据集和中规模的数据集(几个million-几十个million),基于LSH的方法的效果和性能都还不错。这方面有2个开源工具FALCONN和NMSLIB。
- 矢量量化方法
- 矢量量化方法,即vector quantization。在矢量量化编码中,关键是码本的建立和码字搜索算法。比如常见的聚类算法,就是一种矢量量化方法。而在相似搜索中,向量量化方法又以PQ方法最为典型。
- 对于大规模数据集(几百个million以上),基于矢量量化的方法是一个明智的选择,可以用用Faiss开源工具。
3. Product Quantization算法的核心
文献[1]详细介绍了PQ算法的过程和时间复杂度分析,这篇博客的第3节和第4节简要总结下其中的若干要点。
在介绍PQ算法前,先简要介绍vector quantization。在信息论里,quantization是一个被充分研究的概念。Vector quantization定义了一个量化器quantizer,即一个映射函数q,它将一个D维向量x转换码本cookbook中的一个向量,这个码本的大小用k表示。
Quantization is a destructive process which has been extensively studied in information theory. Its purpose is to reduce the cardinality of the representation space, in particular when the input data is real-valued. Formally, a quantizer is a function q mapping a D-dimensional vector x∈RD to a vector q(x)∈C=ci;i∈I, where the index set I is from now on assumed to be finite: I=0,⋯,k−1. The reproduction values ci are called centroids. The set of reproduction values C is the codebook of size k.
如果希望量化器达到最优,那么需要量化器满足Lloyd最优化条件。而这个最优量化器,恰巧就能对应到机器学习领域最常用的kmeans聚类算法。需要注意的是kmeans算法的损失函数不是凸函数,受初始点设置的影响,算法可能会收敛到不同的聚类中心点(局部最优解),当然有kmeans++等方法来解决这个问题,对这个问题,这篇文章就不多做描述。一般来说,码本的大小k一般会是2的幂次方,那么就可以用log2k bit对应的向量来表示码本的每个值。
有了vector quantization算法的铺垫,就好理解PQ算法。其实PQ算法可以理解为是对vector quantization做了一次分治,首先把原始的向量空间分解为m个低维向量空间的笛卡尔积,并对分解得到的低维向量空间分别做量化,那如何对低维向量空间做量化呢?恰巧又正是用kmeans算法。所以换句话描述就是,把原始D维向量(比如D=128)分成m组(比如m=4),每组就是D∗=D/m维的子向量(比如D∗=D/m=128/4=32),各自用kmeans算法学习到一个码本,然后这些码本的笛卡尔积就是原始D维向量对应的码本。用qj表示第j组子向量,用Cj表示其对应学习到的码本,那么原始D维向量对应的码本就是C=C1×C2×…×Cm。用k∗表示子向量的聚类中心点数或者说码本大小,那么原始D维向量对应的聚类中心点数或者说码本大小就是k=(k∗)m。可以看到m=1或者m=D是PQ算法的2种极端情况,对m=1,PQ算法就回退到vector quantization,对m=D,PQ算法相当于对原始向量的每一维都用kmeans算出码本。
The strength of a product quantizer is to produce a large set of centroids from several small sets of centroids: those associated with the subquantizers. When learning the subquantizers using Lloyd’s algorithm, a limited number of vectors is used, but the codebook is, to some extent, still adapted to the data distribution to represent. The complexity of learning the quantizer is m times the complexity of performing k-means clustering with k∗ centroids of dimension D∗.
如图1所示,论文作者在一些数据集上调试k∗和m,综合考虑向量的编码长度和平方误差,最后得到一个结论或者说默认配置,k∗=256和m=8。像这样一种默认配置,相当于用 m×log2k∗=8×log2256=64 bits=8 bytes来表示一个原始向量。图2是在这个默认配置下对128维的原始数据用PQ算法的示意图。
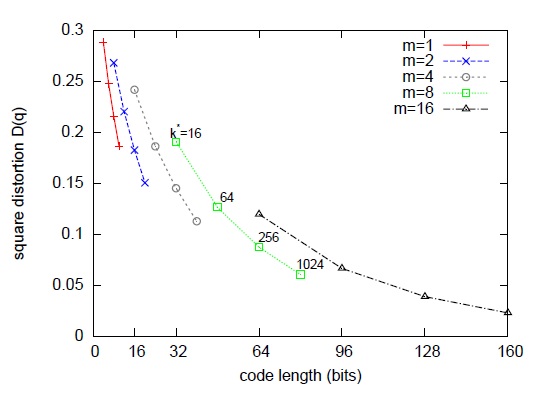
图1 量化误差与m和k*之间的关系
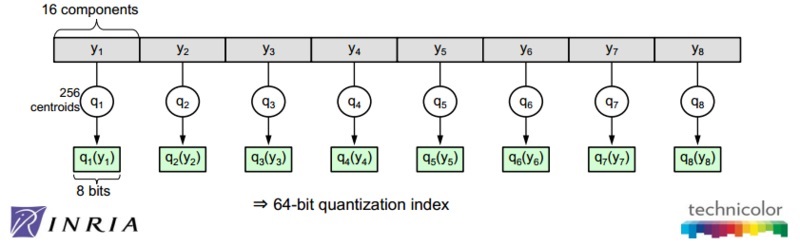
图2 PQ算法的示意图
上面介绍了如何建立PQ的量化器,下面将介绍如何基于这些量化器做相似搜索。有2种方法做相似搜索,一种是SDC(symmetric distance computation),另一种是ADC(asymmetric distance computation)。SDC算法和ADC算法的区别在于是否要对查询向量x做量化,参见公式1和公式2。如图3所示,x是查询向量(query vector),y是数据集中的某个向量,目标是要在数据集中找到x的相似向量。
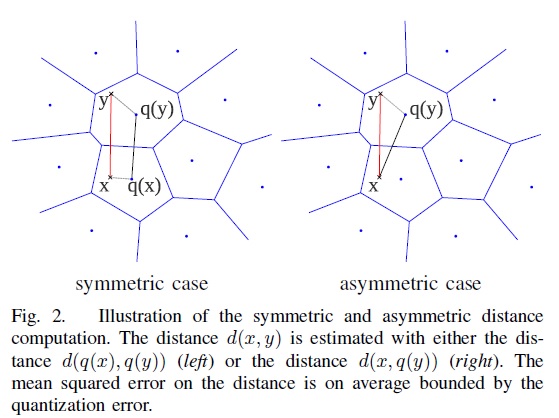
图3 SDC和ADC的示意图
SDC算法:先用PQ量化器对x和y表示为对应的中心点q(x)和q(y),然后用公式1来近似d(x,y)。
对SDC的2点补充说明:
- 为提高计算速度,一般会提前算好d(cj,i,cj,i′)2,然后在检索时就是查表,以O(1)的复杂度查出结果。
- d^(x,y)是d(x,y)的近似计算,一般会先用相似计算方法选出top N近邻,然后再做rerank以拿到最终的近邻排序结果。
ADC算法:只对y表示为对应的中心点q(y),然后用公式2来近似d(x,y)。
对ADC的2点补充说明:
- 为提高计算速度,一般会在检索前提前算好d(uj(x),cj,i)2:j=1,⋯,m,i=1,⋯,k∗,然后在检索时就是查表,以O(1)的复杂度查出结果。
- d˜(x,y)也是d(x,y)的近似计算,与SDC类似,一般会先用相似计算方法选出top N近邻,然后再做rerank以拿到最终的近邻排序结果。
图4对比了SDC算法和ADC算法的各阶段复杂度,当n>k∗D∗时,计算瓶颈存在于公式1和公式2的计算上,它们的复杂度都是O(n×m)。

图4 对比SDC和ADC的各阶段计算复杂度
文献[1]还对SDC和ADC算法做了两点更深入的分析,第一点是对距离的期望误差的上界进行分析。对ADC算法而言,距离的期望误差的上界只与量化误差有关,与输入的x无关,而对SDC算法而言,距离的期望误差的上界是ADC距离的期望误差的上界的两倍,所以作者建议在应用时倾向于用ADC算法。作者做的第二点分析是计算距离的平方的期望,并希望通过矫正拿到距离的无偏估计。作者虽然推导出校准项,但在实验中却发现加上校准项反倒使得距离的残差的方差加大了,所以作者建议在应用时倾向于不加校准项,也就是说还是用公式1或者公式2做计算。
4. Product Quantization算法的改进
第3节介绍了SDC和ADC算法,当n>k∗D∗时,计算瓶颈存在于公式1和公式2的计算上,它们的复杂度都是O(n×m)。实际中n可能是千万量级甚至更大,虽然相比暴力搜索算法,PQ算法已经减少了计算量,但计算量依旧很大,并不实用。所以作者提出了IVFADC算法,一种基于倒排索引的ADC算法。简而言之,该算法包含2层量化,第1层被称为coarse quantizer,粗粒度量化器,在原始的向量空间中,基于kmeans聚类出k′个簇(文献[8]建议k′=n−−√)。第2层是上文讲的PQ量化器,不过这个PQ量化器不是直接在原始数据上做,而是经过第1层量化后,计算出每个数据与其量化中心的残差后,对这个残差数据集进行PQ量化。用PQ处理残差,而不是原始数据的原因是残差的方差或者能量比原始数据的方差或者能量要小。图5是该方法的索引和查询的流程图。
The energy of the residual vector is small compared to that of the vector itself.
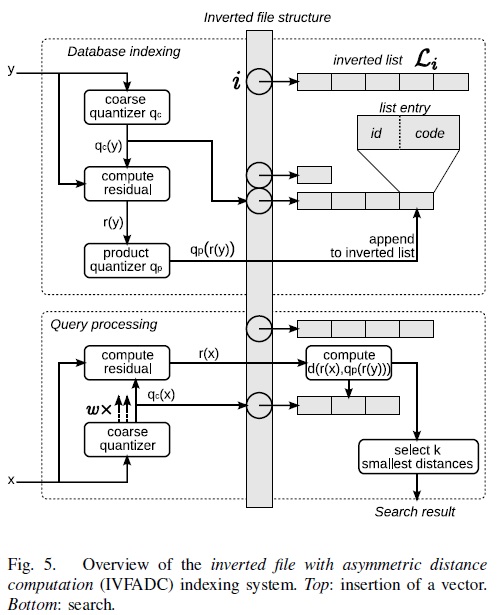
图5 IVFADC算法的索引和查询的流程图
对IVFADC的3点补充说明:
- 考虑到在coarse quantization中,x和它的近邻不一定落在同一个簇中,所以在查询coarse quantization时,会同时取出w个倒排链。
- 对取出的每个倒排链,还是用第3节介绍的PQ算法把近邻给找出。
- 考虑当n>k∗D∗时,朴素的ADC算法的复杂度是O(n×m),而IVFADC算法的复杂度会降低为O((n×w/k′)×m)。
参考文献
[1] Product quantization for nearest neighbor search
[2] Efficient matching and indexing
[3] 百度NLP | 神经网络模型压缩技术
[4] Faiss
[5] 图像检索:再叙ANN Search
[6] What are some fast similarity search algorithms and data structures for high-dimensional vectors?
[7] Locality-Sensitive Hashing: a Primer
[8] Billion-scale similarity search with GPUs
[9] 解读Product quantization for nearest neighbor search
这篇关于PQ(product quantization) 算法---(一)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








