本文主要是介绍986: 哈夫曼译码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

解法:先把代码粘贴到编译器(vs)上,分享一个一键去除空白行的操作,ctrl+f调出查找窗口,输入查找(?<=\r\n)\r\n,选择正则表达式,替换就可以发现会去掉一百多行空白行。
本题只需要利用得到的哈夫曼码去译码即可。
推荐先学这个【数据结构与算法】-哈夫曼树(Huffman Tree)与哈夫曼编码_哈夫曼树编码-CSDN博客
要看 得到的哈夫曼树是什么样子
只需要加上
void print_haffman(haffnode ht[],int n) {cout << "下标i" << " ";cout << "ch" << " ";cout << "weight" << " ";cout << "flag" << " ";cout << "parent" << " ";cout << "leftchild" << " ";cout << "rightchild" << " ";cout << endl;for (int i = 0; i < 2 * n - 1; i++) {cout <<" "<< i << " ";cout << ht[i].ch << " ";cout << ht[i].weight << " ";cout << ht[i].flag << " ";cout << ht[i].parent << " ";cout << ht[i].leftchild << " ";cout << ht[i].rightchild << " ";cout << endl;}
}得到

一下子就可以画出哈夫曼树出来

要看 得到的哈夫曼译码表
只需加上
void print_haffmancode(code hc[], int n) {for (int i = 0; i < n; i++) {cout << hc[i].ch << " ";for (int j = hc[i].start+1; j < n; j++) {cout << hc[i].bit[j];}cout << endl;}
}得到

回归正题。
译码(以a0001举例)
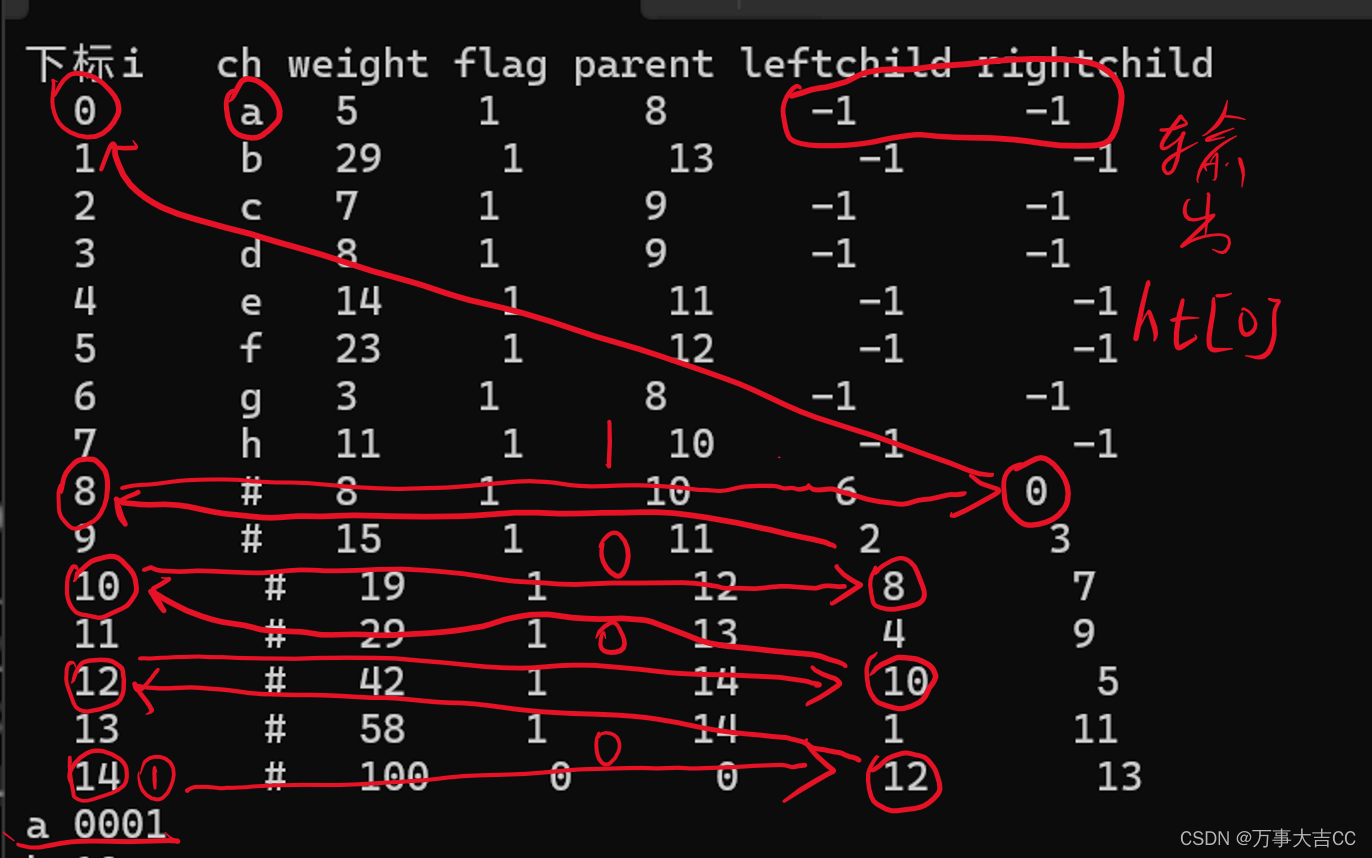
算法就是:遍历i给定01串,j每次从下标2*n-2开始回溯到0,若达到叶子节点也就是左右孩子为空,则打印ht[j]且重置j,否则继续遍历。
代码
void ccode(haffnode ht[], int n)
{ string s;cin >> s;int j = 2 * n - 2;for (int i = 0; i < s.size(); ) {while (ht[j].leftchild!=-1 || ht[j].rightchild!=-1) {if (s[i] == '0')j = ht[j].leftchild;elsej = ht[j].rightchild;i++;}cout << ht[j].ch;j = 2 * n - 2;}
}这篇关于986: 哈夫曼译码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!