北京大学肖臻老师《区块链技术与应用》P16(状态树)和P17(交易树和收据树)

2024-05-09 13:28
文章标签 肖臻 p16 p17 区块 收据 北京大学 老师 应用 状态 交易 技术

本文主要是介绍北京大学肖臻老师《区块链技术与应用》P16(状态树)和P17(交易树和收据树)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1️⃣ 参考

  • 北京大学肖臻老师《区块链技术与应用》
    • P16 - ETH状态树篇
    • P17 - ETH交易树和收据树篇
  • 部分文字和图片
    • 北京大学肖臻老师《区块链技术与应用》公开课笔记18——ETH数据结构篇2(状态树2)
    • 北京大学肖臻老师《区块链技术与应用》公开课笔记19——ETH数据结构篇3(交易树和收据树)

1️⃣6️⃣ 状态树

① 引言

  • 回顾
    • 以太坊账户地址为160bits（20字节），表示为40个16进制数
    • 状态包含了
      • 余额(balance)
      • 交易次数(nonce)
      • 合约账户中还包含了代码(code) 和 存储(stroge)
    • 在比特币和以太坊系统中，核心单位是区块，是通过区块构成区块链，交易是保存在区块内部
    • 在脑中要有一个意识，每个人都可以在本地构建区块链，只是像在比特币系统中上链的区块是矿工说的算，其他人复制

现在要实现从账户地址到账户状态的映射，咋一看，容易想到Key-value键值对，所以直观想法便用哈希表实现。若不考虑哈希碰撞，查询直接为常数级别的查询效率。

但采用哈希表，难以提供Merkle proof(需要回顾请看这里)

  • Merkle Tree
    • 作用
      • 提供证明账户上余额
      • 维护全节点之间状态的一致性（对于当前区块中包含了哪些交易，全节点之间要有共识）
    • 缺点
      • 没有提供一个高效的查找和更新的方法

思考

  • 比特币为什么可以构建Merkle Tree，而以太坊不行 ？
    1. 因为构建的内容不是一个量级的
      • 在比特币系统中，仅对一个区块中的交易(最多包含4000左右) 构造，前面构建好的是不发生变化的
      • 在以太坊系统中，基于账户的模式下，每发布一个区块，要将所有的账户都遍历一遍来构建，开销太大。
    2. 构建出的Merkle Tree不唯一
      • 在比特币系统中，没有排序不影响，因为是一人(拥有记账权的矿工 POW)说的算，其他都都是复制，所以大家得到的Merkle Tree是唯一的
      • 在以太坊系统中，因为没有排序，没办法保证新账户出现在叶子节点的顺序（因为每个人接受新节点的顺序是不一样的），算出的根哈希值不同，所以构建的Merkle Tree不唯一

思考

  • 那么经过排序，使用Sorted Merkle Tree可以吗？
    • 还是开销太大，新增账户，由于其地址随机，插入Merkle Tree时候很大可能在树中间，发现其必须进行重构。（牵一发而动全身）

所以，简单的Merkle Tree和哈希表数据结构是不满足的
那么我们看一下实际中以太坊采取的数据结构：MPT(第四小节)

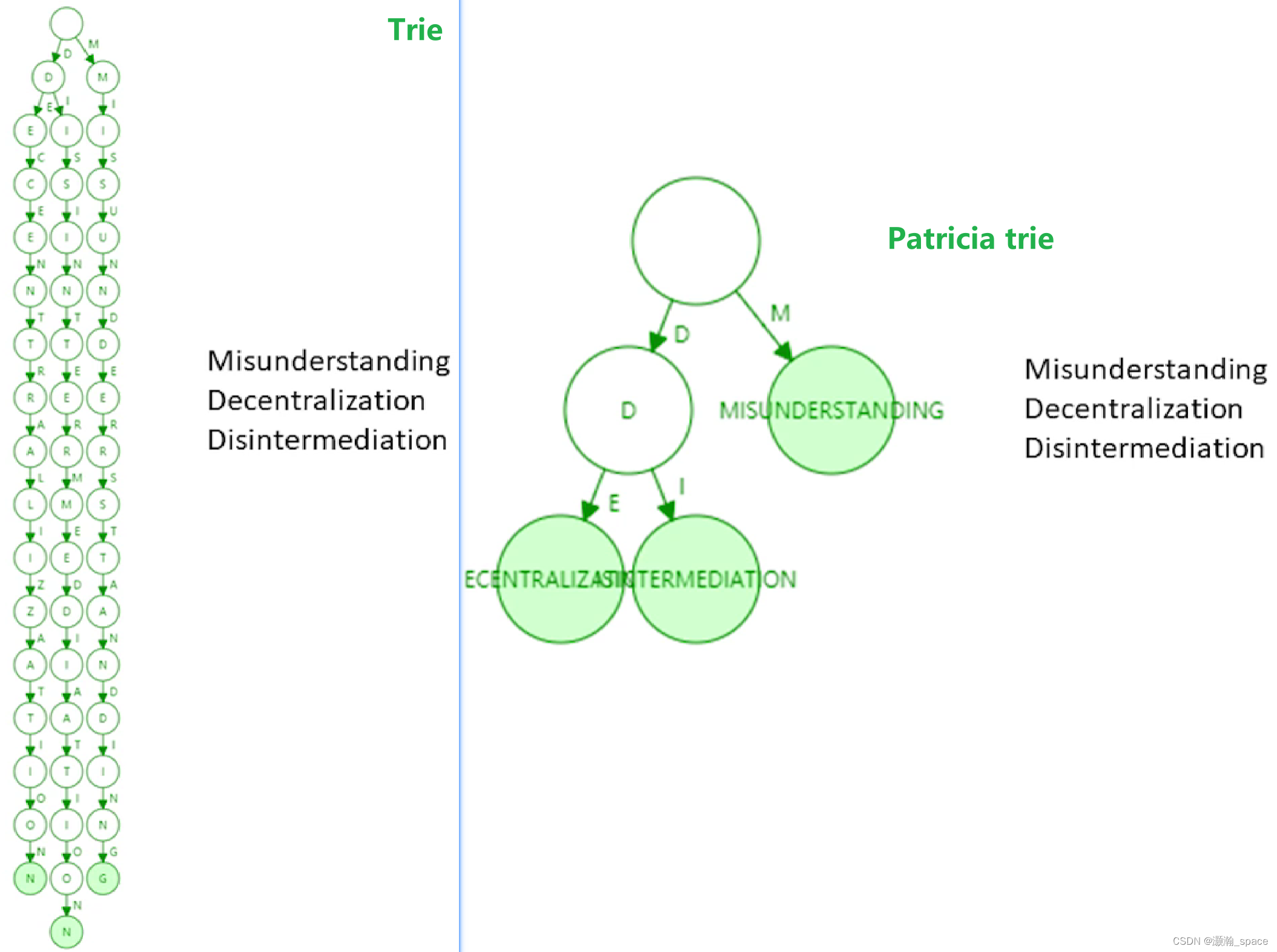
② trie(字典树、前缀树)

  • 取自单词retrieval n. 检索

  • 下图是使用trie数据结构对单词进行存储
    请添加图片描述

  • trie特点：

    • trie中每个节点的分支数目取决于Key值中每个元素的取值范围【图例中最多26个英文字母分叉 + 一个结束标志位；以太坊中最多17，16进制(0 ~ f) + 1结束符】。
    • trie查找效率取决于key的长度。实际应用中每个地址长度都是相同的
    • 理论上哈希会出现碰撞，而trie上面不会发生碰撞。
    • 给定输入后构造的trie都是一样的（无论如何顺序插入）。
    • 更新操作的局部性较好（只用更新其分支，其他不变）
  • trie缺点：
    • trie的存储浪费，很多节点只存储一个key(叶子节点)。因此，要是能合并一些就好了，为此，引入了Patricia tree/trie

③ Patricia trie(经过路径压缩的前缀树，压缩前缀树)

  • 下图为压缩后，明显树的高度变得浅了，访问内存的次数将会大大减少，提高了效率
    请添加图片描述

需要注意的是，如果新插入单词，原本压缩的路径可能需要扩展开来。

问题

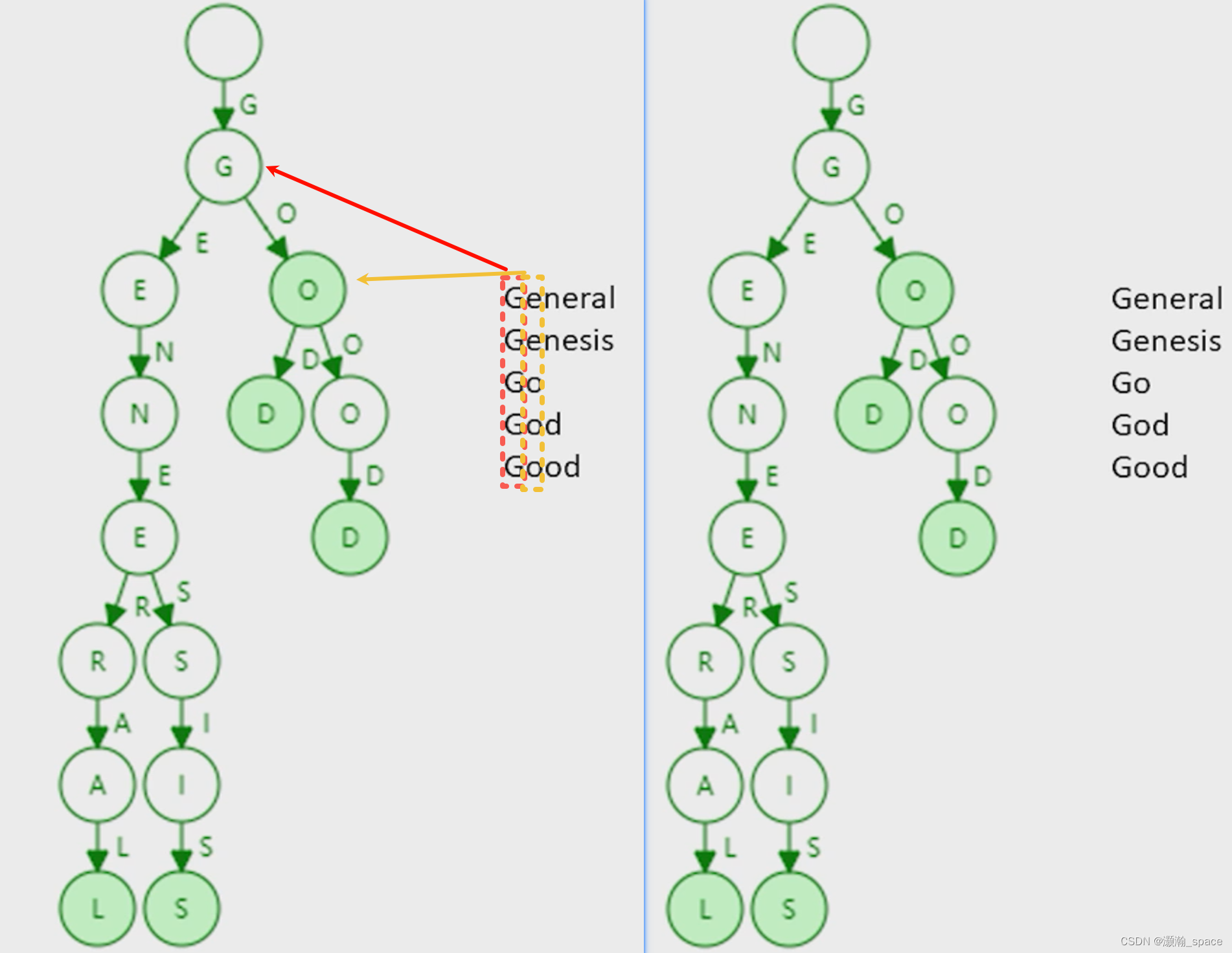
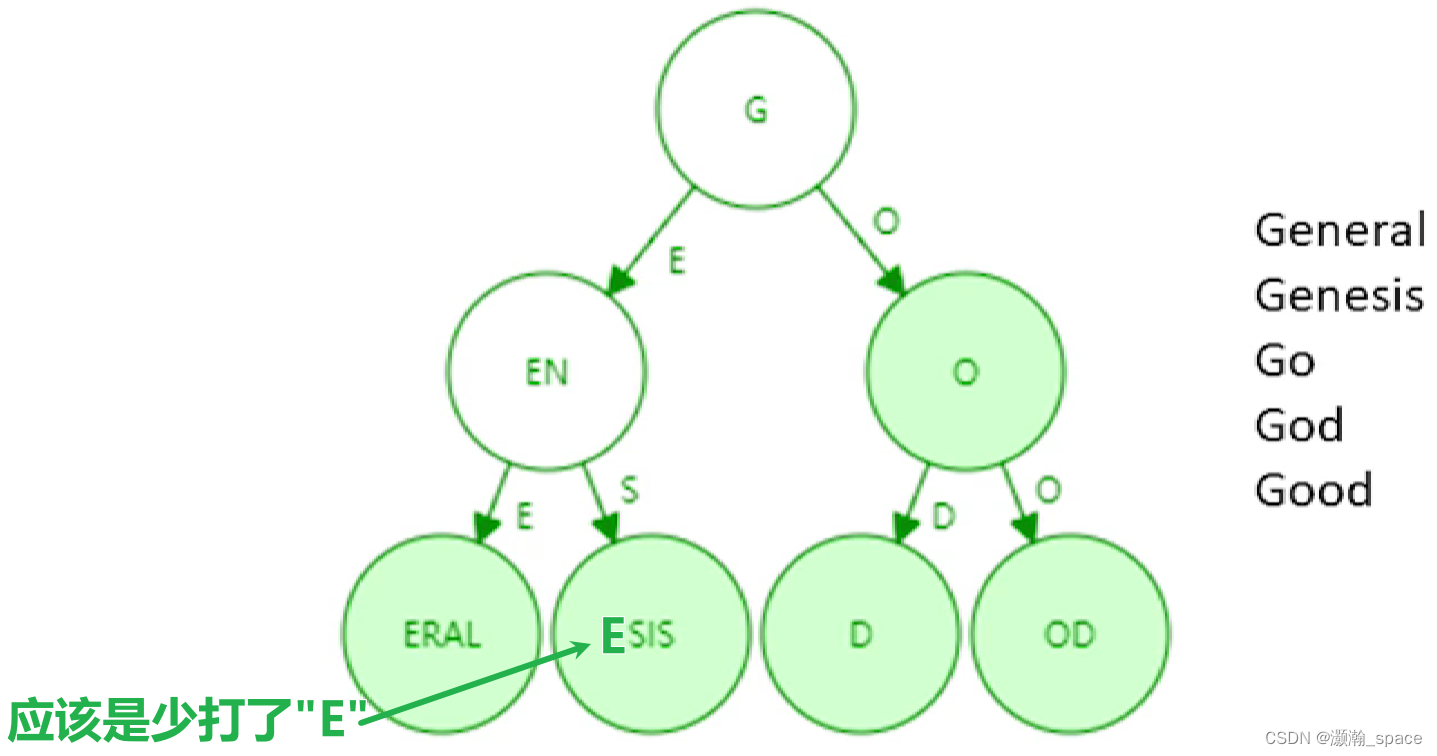
  • 那么，需要考虑什么情况下路径压缩效果较好？
    • 树中插入的键值分布较为稀疏的情况下，可见路径压缩效果较好（如下图）。
      Disintermediation 去中间商请添加图片描述

在以太坊系统中，160位的地址存在 2 160 2^{160} 2160 种，和账户数目相比，可以认为地址这一键值非常稀疏。因此，我们可以在以太坊账户管理种使用Patricia trie这一数据结构

  • 为什么要设计的非常稀疏？
    • 防止地址发生碰撞，也就是防止账户冲突

但实际上，在以太坊种使用的并非简单的PT(Patricia trie),而是MPT(Merkle Patricia trie)

④ MPT(Merkle Patricia trie)

  • Merkle tree 与 Binary tree 区别
    • 区块链和普通链表的区别在于把普通指针换成了哈希指针
    • 同样，Merkle tree 相比 Binary tree，也是普通指针换成了哈希指针

  • block header中的根哈希值

    • BTC的block header只有一个根哈希值：
      • 区块中的交易组成的Merkle tree的根哈希值
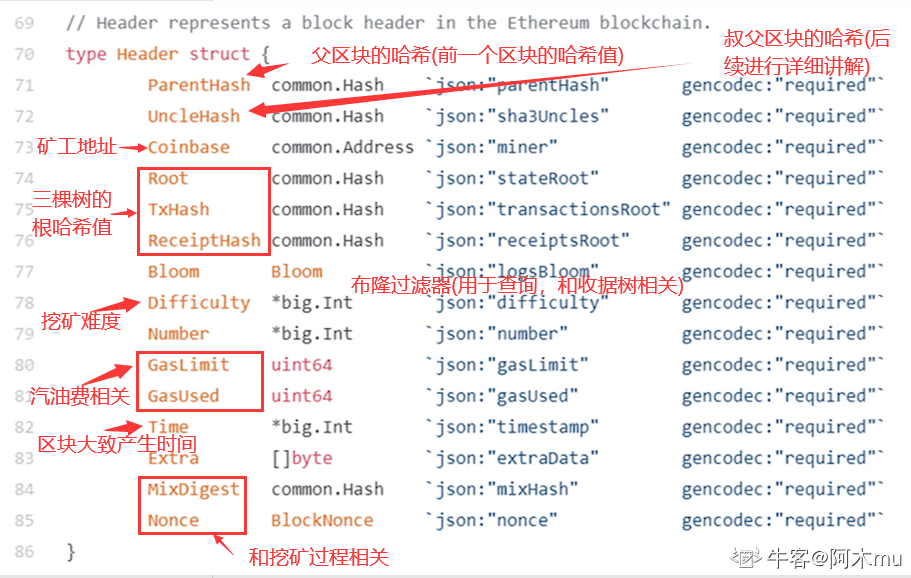
    • ETH的block header中有三个根哈希值：
      • 交易树的根哈希值：由区块中交易组成
      • 状态树的根哈希值：将所有账户组织为一个经过路径压缩和排序的Merkle Tree
      • 收据树的根哈希值：后面会展开

  • 根哈希值的用处：

    • 防篡改
    • 提供Merkle proof给轻节点可以验证账户余额
    • 证明某个发生了交易的账户是否存在

⑤ MMPT(Modified Merkle Patricia trie)

⑤① MMPT的图示

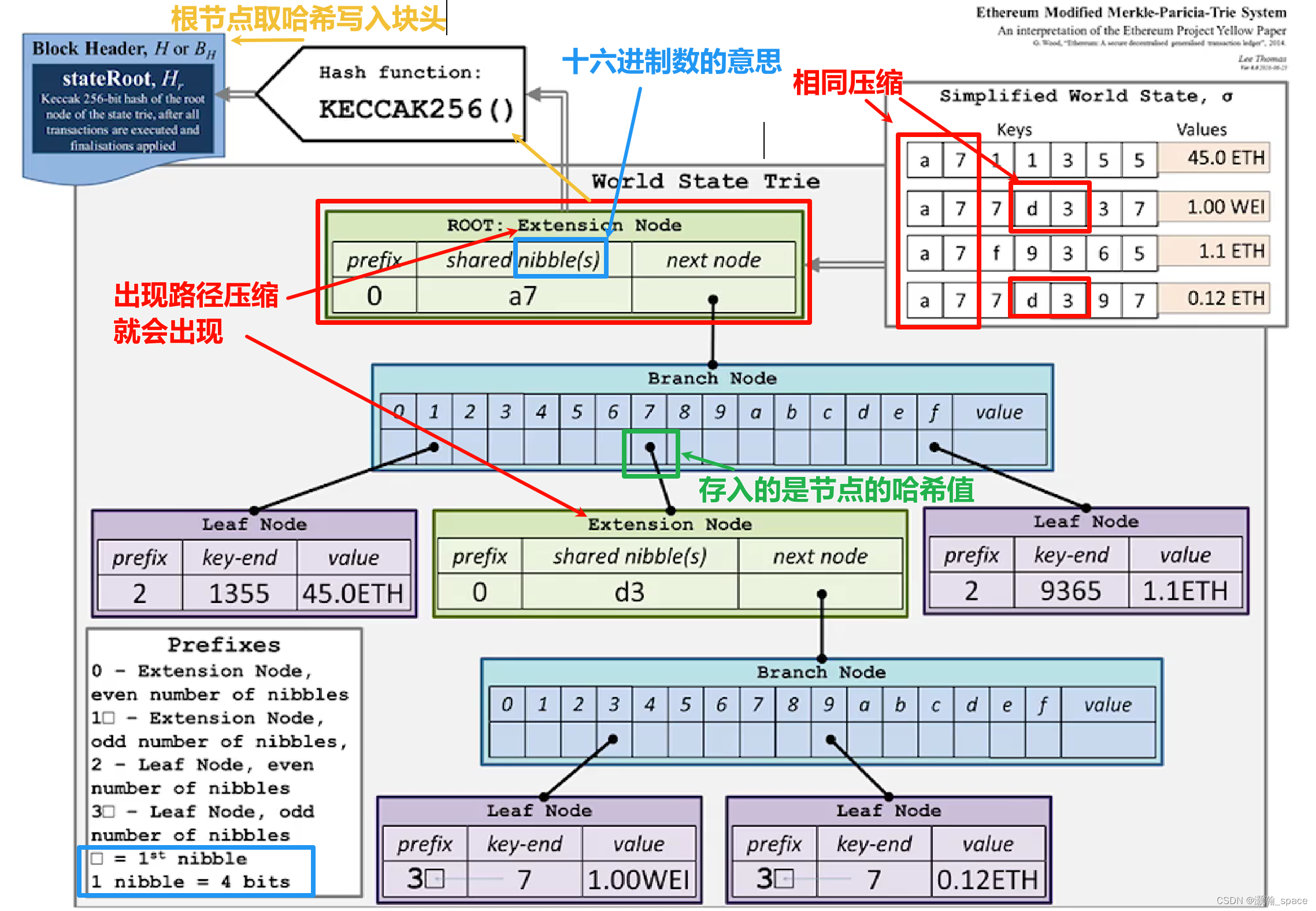
请添加图片描述

  • 与普通的Merkle Patricia trie不同在哪？
    • Prefixes有分奇数哥和偶数个nibble

⑤② MMPT的运用

发布新区块的时候，状态树中有一些节点的值会发生变化，这些改变是在保留原来状态基础上新建分支来修改

在这里插入图片描述

  • 虽然有两颗状态树，但大部分节点是共享的
  • 以太坊的结构是大的MMPT包含小的MMPT，每个合约账户的存储中也是一颗MMPT
  • 所以，系统中全节点并非维护一棵MPT，而是每次发布新区块都要新建MPT，只不过大部分节点共享，只有少数发生变化的节点要新建分支
  • 为什么要保存原本状态？为何不直接修改？
    • 便于回滚。因为以太坊支持智能合约，智能合约中的代码时很复杂的，没办法从中倒推出执行合约前的状态，所以要想支持回滚，就必须保存历史状态

⑥ 以太坊数据结构源码

⑥① block header

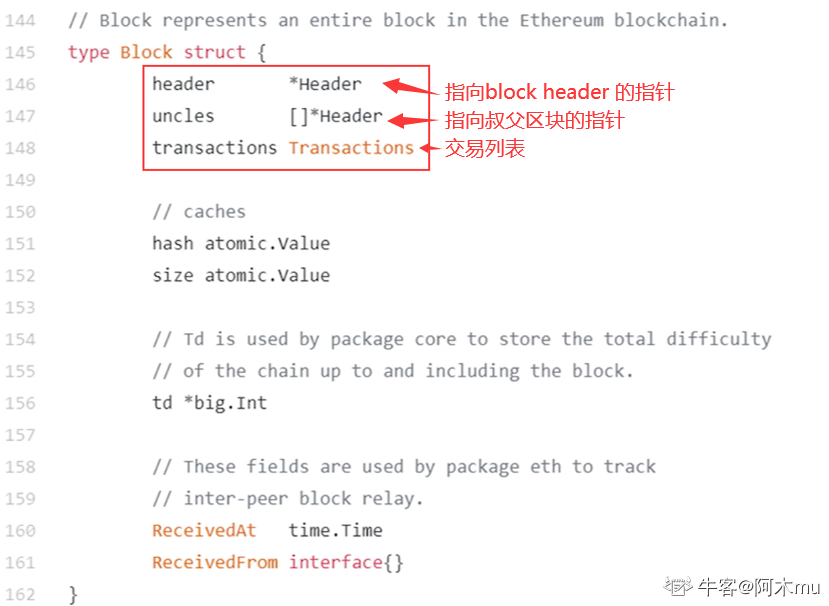
⑥② 区块结构

⑥③ 区块在网上真正发布时的信息

在这里插入图片描述

⑦ 状态树中的value

状态树中保存Key-value对，key是地址，value是状态通过RLP(Recursive Length Prefix，一种进行序列化的方法)编码序列号之后再进行存储。

以太坊的所有类型最后都要经过RLP变成字符数组(nested array of bytes)

1️⃣7️⃣ 交易树和收据树

  • 每次发布一个区块时，区块中的交易会形成一颗交易树
  • 以太坊还添加了收据树，在每个交易执行完之后形成一个收据，记录交易相关信息。
  • 也就是说，使交易树和收据树上的节点是一一对应的。
  • 为什么要有收据树？
    • 因为智能合约执行较为复杂，通过收据树，有利于快速查询执行结果。

  • 以太坊中三棵树都是Merkle Patricia trie，MPT的优点是支持查找操作，通过键值

    • 状态树键值与特点
      • 将所有账户的状态都包含进去（无论这些账户是否与当前区块中交易有关系）
      • 多个区块状态树共享节点
      • 查找键值为账户地址
    • 交易树和收据树键值与特点
      • 只将当前区块中的交易组织起来
      • 依照区块独立
      • 查找键值为交易在发布的区块中的序号

  • 比特币只有一颗交易树，采用普通的MT(Merkle Tree)

  • 交易树和收据树的用途：
    • 向轻节点提供Merkle Proof
      • 交易树证明：某个交易被打包到节点中
      • 收据树证明：某个交易的执行结果
    • 更加复杂的查找操作，例如：查找过去十天的跟某个智能合约的交易

以太坊中是如何实现这复杂的查找操作呢？ 答：Bloom filter(布隆过滤器)

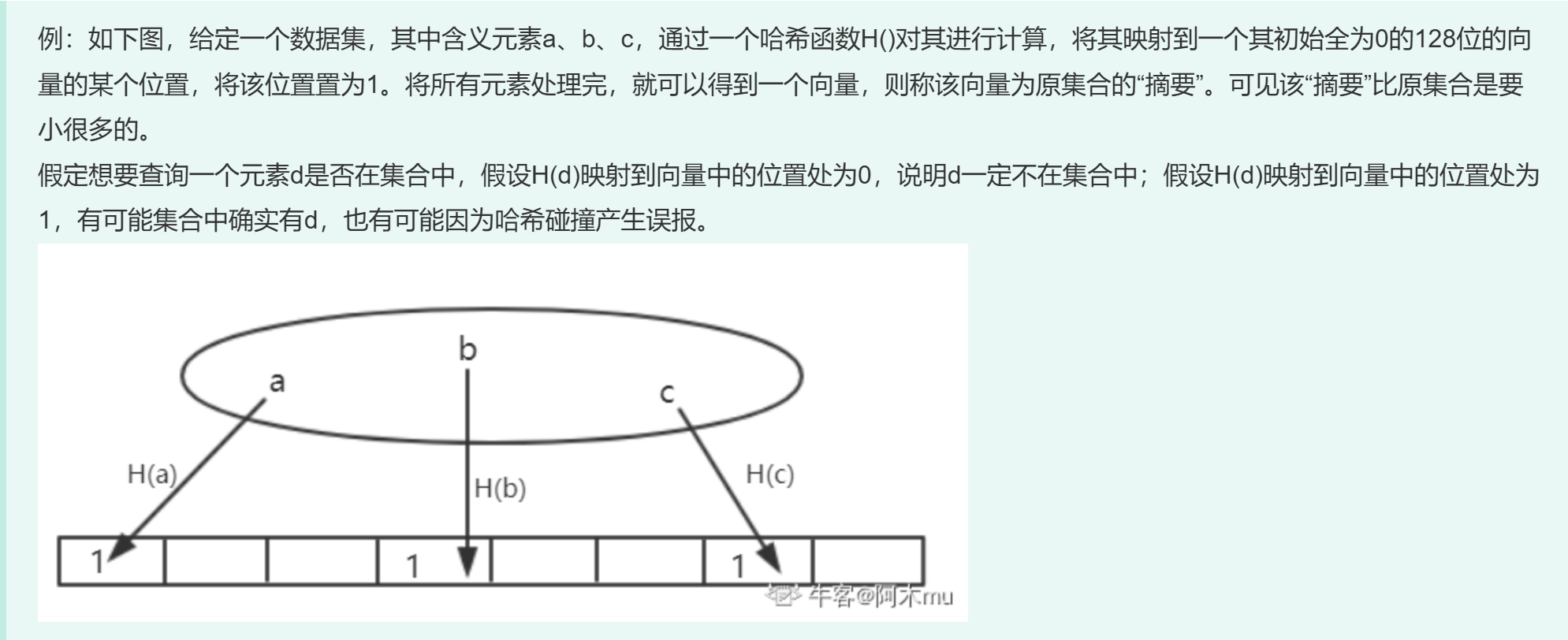
① Bloom Filter(布隆过滤器)

布隆过滤器可以判断某个数据一定不存在，但是无法判断一定存在(可能发生互相碰撞，false positive)

  • 功能：支持较为高效查找某个元素是否在某个集合中
  • 实现：计算出一个紧凑的“摘要”。将每个个元素都取哈希，找到向量中的对应位(初始化全为0)，然后置为1，全部元素处理完后就得到原来集合的摘要
  • 例子
    在这里插入图片描述
  • 如何删除集合中元素？
    • 没法操作。也就是说，简单的Bloom filter不支持删除操作。如果想要支持删除操作，需要将记录数不能为0和1，需要修改为一个计数器来记录这个位置有多少元素映射，而且还需要考虑计数器是否会溢出。

② 以太坊中的Bloom filter

  • 每个交易完成后会产生一个收据，收据中包含一个Bloom filter，用于记录交易类型、地址等信息

  • 发布的区块中块头里有一个总Bloom filter，其为该区块中所有交易的Bloom filter的一个并集

  • 查找时候先查找哪个区块块头中包含需要的Bloom filter，（如果不包含，则一定不存在）如果块头中包含，再查找区块中包含的交易所对应的收据树中的Bloom filter，也就是每个收据的Bloom filter，看看哪个有，再查看交易进行确认；也可能都没有，因为可能是false positive

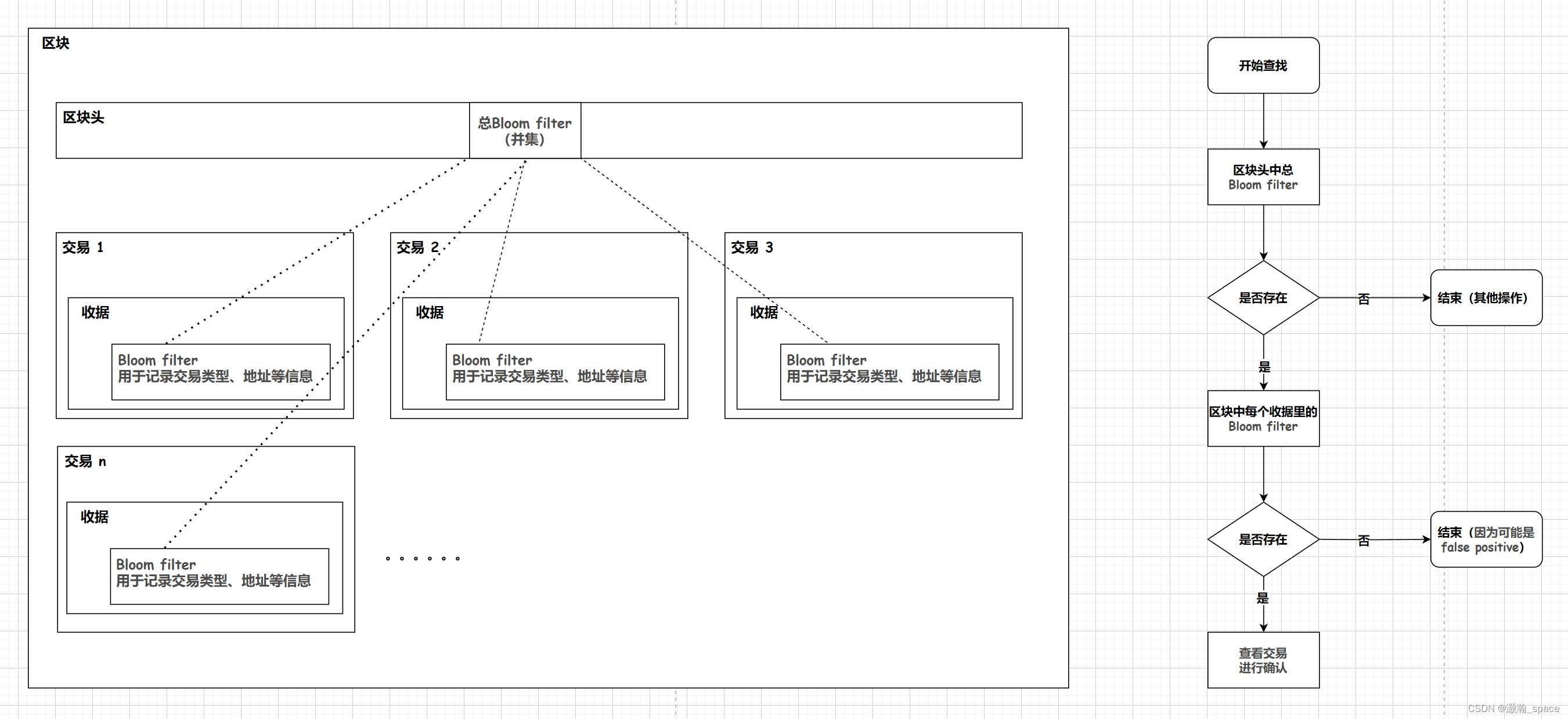
在这里插入图片描述

  • 这样设计Bloom filter结构的优点：
    • 快速大量过滤掉大量无关区块，从而提高了查找效率。（可以过滤掉很多轻节点，若想进一步确认，再向全节点请求信息）

③ 状态机

以太坊的运行过程，可以视为交易驱动的状态机(transaction-driven state machine)，通过执行当前区块中包含的交易，驱动系统从当前状态转移到下一状态。当然，BTC我们也可以视为交易驱动的状态机，其状态为UTXO（用掉一些输出，又会增加一些新的输出，所以发布的区块会驱动状态机从当前的状态转移到下一个状态）。

  • 状态机的共同特点：状态转移是确定性的
    • 对于给定的当前状态和给定一组交易，可以确定性的转移到下一状态(保证系统一致性)。

问题1：

  • 有没有可能收款账户不包含再状态树中？
    • 可能
    • 因为在以太坊和比特币系统中，新建的账户是不会被知道的，只有产生交易时才会被系统知道，对应在以太坊的操作是在状态树中新插入一个节点

问题2：

  • 能否将每个区块中状态树改成只包含和区块中交易相关的账户状态？(这样就和交易树、收据树保持一致，可以大幅削减状态树大小）
    • 不能
    • 这样的设计账户状态查找不方便，因为不存在某个区块包含所有状态
      • 例如，查询新建账户的状态，则需要一直找到创世纪块才能知道这个账户不存在是个新建的账户😅，而区块链是不断延长的。

④ 交易树和收据树的创建过程(代码)

  • NewBlock()

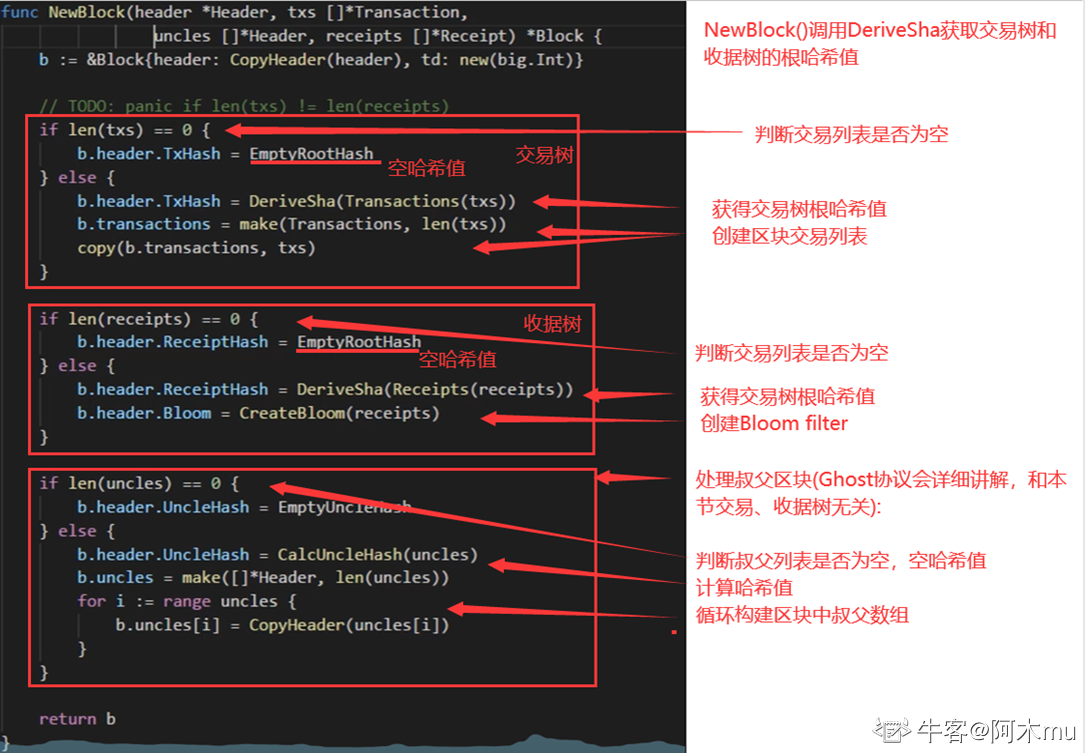
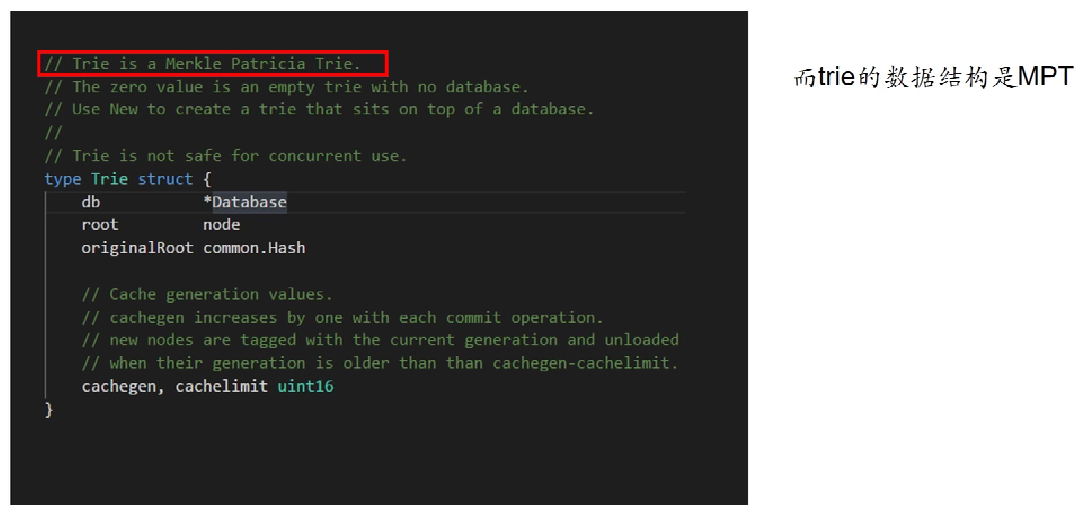
  • DeriveSha()

在这里插入图片描述

  • Trie struct

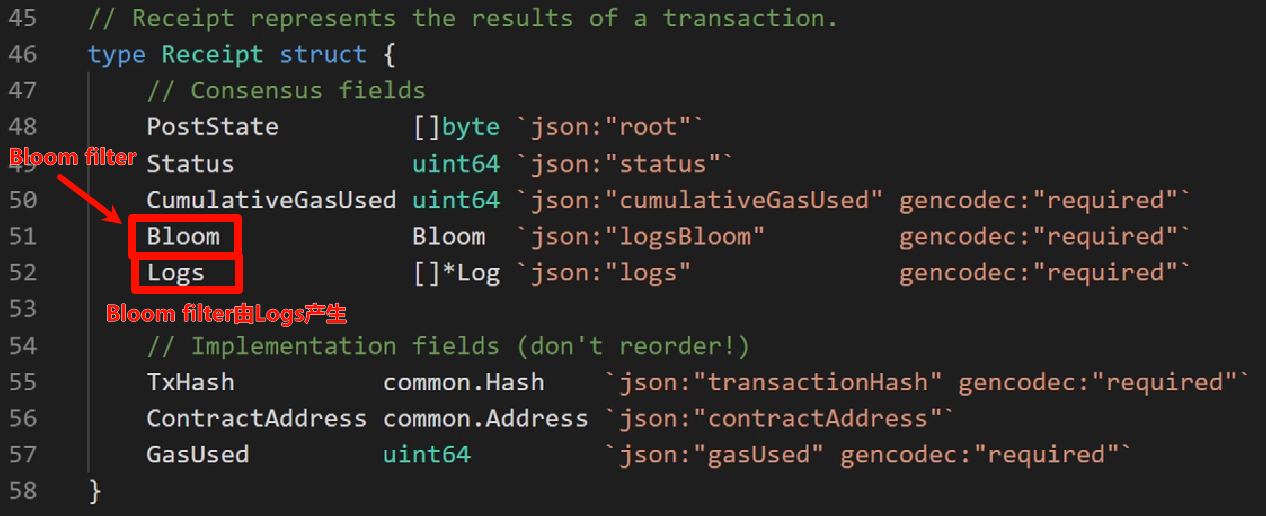
在这里插入图片描述

  • Receipt struct
    + 每个交易执行完后形成的收据

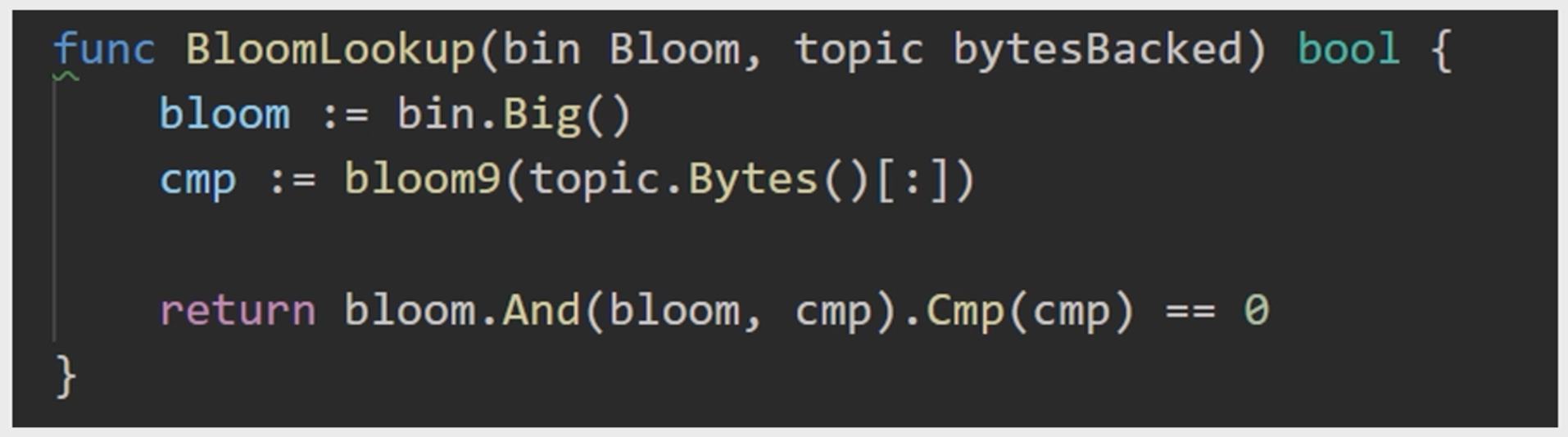
在这里插入图片描述

  • 创建Bloom filter

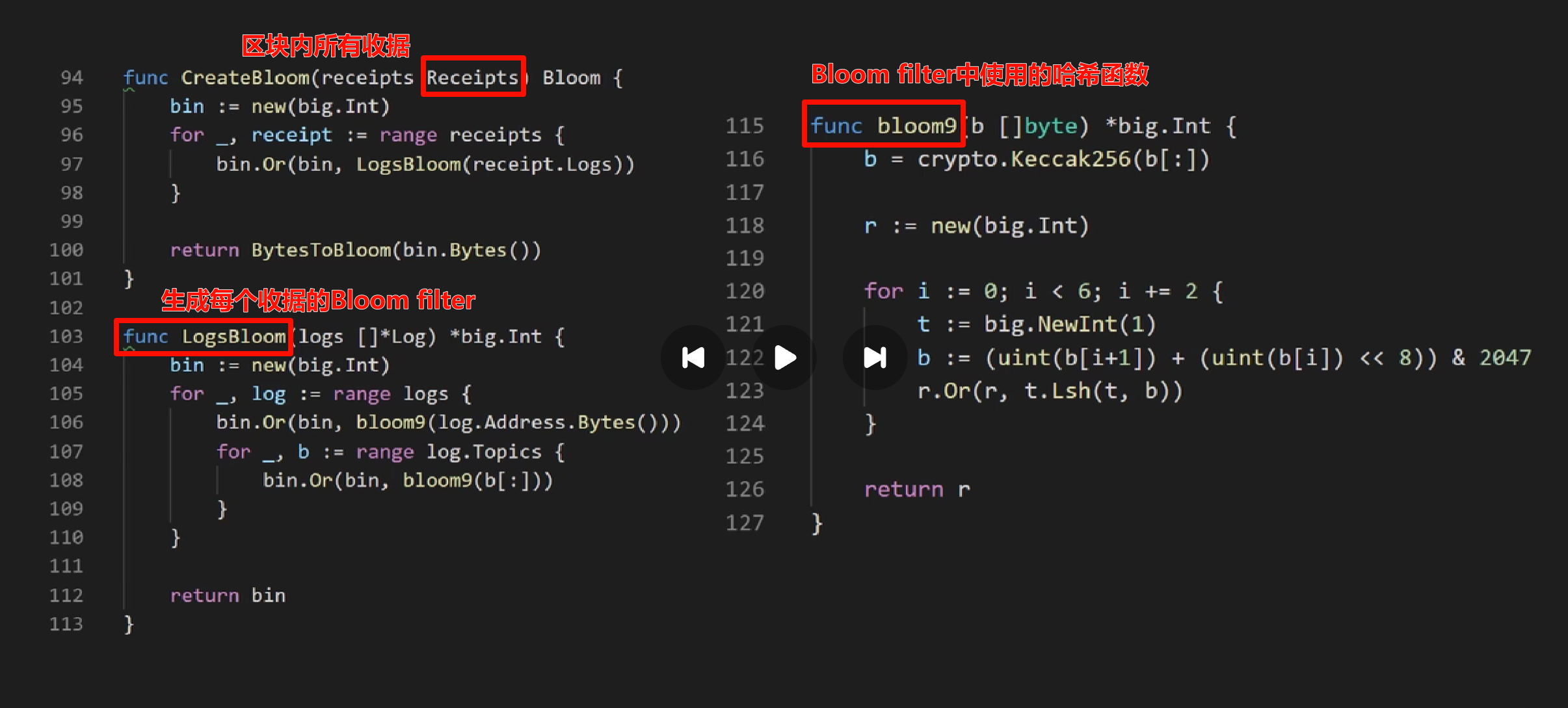
在这里插入图片描述

  • 使用Bloom filter查询查询topic(交易类型、地址等信息)

在这里插入图片描述

这篇关于北京大学肖臻老师《区块链技术与应用》P16(状态树)和P17(交易树和收据树)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/973545。

相关文章

XMLHttpRequest对象的status属性状态吗

XMLHttpRequest对象的status属性状态吗

在做异步操作的时候，我们通常需要判断返回的状态码来判断服务器返回的数据是否正常，下面是常见的一些状态码和对应的含义。 状态码 200服务器正常处理了请求并响应404请求的页面（资源）没有找到403没有权限访问请求的页面（资源）405页面（资源）不接收该请求方式（比如用get请求一个只支持doPost方法的servlet）408请求超时500服务器处理请求时遇到错误（可能因为应用程序抛出异
阅读更多...
2019年长沙前端技术分享大会圆满成功

2019年长沙前端技术分享大会圆满成功

做一个积极的人 编码、改bug、提升自己 我有一个乐园，面向编程，春暖花开！ 本文首发: 唐胡子俱乐部，授权发布！ 摘要 长沙百名互联网前端程序员齐聚长沙互联网活动基地（唐胡子俱乐部）。 主办单位：唐胡子俱乐部 支持单位：芒果TV，拓维，湘邮，58到家，御泥坊，兴盛优选，中软国际，长海科技，长沙联通 时 间：2019年5月19日 ----------------------
阅读更多...
学习笔记：从技术到管理，在蜕变中成长

学习笔记：从技术到管理，在蜕变中成长

大家好，我是阿飞云 怕什么真理无穷，进一步有近一步的欢喜 前几天分享了一篇有关于:从程序员到管理团队，分享一些职场管理的心得，相关内容也可点击下面卡片跳转查看。 本文分享一个看到过的视频内容，视频分享人是 特赞科技 CTO 黄勇，做了关于《从技术到管理，在蜕变中成长》的主题分享，对做技术与做管理的不同，到如何把事情做好有哪些模式，以及团队作战能力方面做了深入的分析。 看完后觉得挺有收获的，学习
阅读更多...
bimface 模型集成-后端（java）上传、发起转换、获取转换状态

bimface 模型集成-后端（java）上传、发起转换、获取转换状态

目录 前言后端架构流程存储表结构全局工具类先根据appid, appsecret 生成accesstoken, 保存到自己的存储服务器。利用保存的 accesstoken 上传模型发起转换获取转换状态根据bimface文件ID获取模型viewtoken, 获取到viewtoken就可以利用前端浏览模型或图纸了 前言 之前没有注意官方有个sdk,然后自己就实现了这么个逻辑。建议
阅读更多...
总结：LayoutInflater和inflate()区别与联系 应用

总结：LayoutInflater和inflate()区别与联系 应用

首先说明的是LayoutInflater和inflate()这两个东东的区别，LayoutInflater是一个公共的抽象类，由object继承而来，而inflate（）是LayoutInflater类的类方法，这一定要弄清楚概念，否则你会晕头转向。然后说这个东东的作用，我们先看看Google的综述： Instantiates a layout XML file into its corres
阅读更多...
SVN下Xcode中文件状态的含义

SVN下Xcode中文件状态的含义

1、代码中 某文件后面有 “M” 标记，表示该文件已被修改，需要 commit. （右键该文件 -> source control -> commit selected file…） 2、代码中 某文件后面有 “A” 标记，表示该文件是新添加的，已受SVN管理，需要 commit. （右键该文件 -> source control -> commit selected file…） 3、代码中 某
阅读更多...
Spring Boot构建应用开发规范

Spring Boot构建应用开发规范

1.规范的意义和作用 •编码规范可以最大限度的提高团队开发的合作效率 •编码规范可以尽可能的减少一个软件的维护成本 , 并且几乎没有任何一个软件，在其整个生命周期中，均由最初的开发人员来维护 •编码规范可以改善软件的可读性，可以让开发人员尽快而彻底地理解新的代码 •规范性编码还可以让开发人员养成好的编码习惯，甚至锻炼出更加严谨的思维 2.代码仓库规范 2.1公共组件 •公共组件通常指
阅读更多...
【应用机器学习】评估一个假设

【应用机器学习】评估一个假设

检验是否过拟合 将数据分成训练集和测试集 通常用70%的数据作为训练集，用剩下30%的数据作为测试集。 很重要的一点是训练集和测试集均要含有各种类型的数据，通常我们要对数据进行洗牌，然后再分成训练集和测试集。 使用训练集对模型进行训练 可以得到一系列参数 theta 使用测试集对模型进行测试 使用测试集数据对模型进行测试，有两种方式计算误差 线性回归模型 利用测试集数据计算代
阅读更多...
Elasticsearch：向量相似度技术和评分

Elasticsearch：向量相似度技术和评分

作者：来自 Elastic Valentin Crettaz 当需要搜索自由文本并且 Ctrl+F / Cmd+F 不再有效时，使用词法搜索引擎通常是你想到的下一个合理选择。 词汇搜索引擎擅长分析要搜索的文本并将其标记为可在搜索时匹配的术语，但在理解和理解被索引和搜索的文本的真正含义时通常会表现不佳。 这正是向量搜索引擎的闪光点。 他们可以对同一文本进行索引，以便可以根据它所代表的含义及其与具
阅读更多...
大模型时代，交换机技术演变、性能分析、衡量指标

大模型时代，交换机技术演变、性能分析、衡量指标

OSI协议及在高性能计算中向RDMA的过渡 协议是为计算机网络内的数据交换而建立的一组规则、标准或协议。在法律层面，OSI七层协议被视为国际标准。该协议于20世纪80年代引入，旨在通过其七层网络模型标准化计算机间通信，以满足开放网络的要求。 物理层规定硬件之间的通信方式，并为物理设备（包括接口类型和传输速率）建立了标准，便于传输比特流（由0和1表示的数据）。 数据链路层主要负责帧编码和错
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2