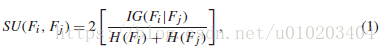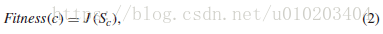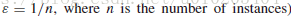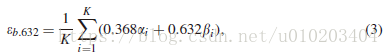马尔可夫毯式遗传算法在基因选择中的应用

本文主要是介绍马尔可夫毯式遗传算法在基因选择中的应用，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

#引用

##LaTex

@article{ZHU20073236,
title = “Markov blanket-embedded genetic algorithm for gene selection”,
journal = “Pattern Recognition”,
volume = “40”,
number = “11”,
pages = “3236 - 3248”,
year = “2007”,
issn = “0031-3203”,
doi = “https://doi.org/10.1016/j.patcog.2007.02.007”,
url = “http://www.sciencedirect.com/science/article/pii/S0031320307000945”,
author = “Zexuan Zhu and Yew-Soon Ong and Manoranjan Dash”,
keywords = “Microarray, Feature selection, Markov blanket, Genetic algorithm (GA), Memetic algorithm (MA)”
}

##Normal

Zexuan Zhu, Yew-Soon Ong, Manoranjan Dash,
Markov blanket-embedded genetic algorithm for gene selection,
Pattern Recognition,
Volume 40, Issue 11,
2007,
Pages 3236-3248,
ISSN 0031-3203,
https://doi.org/10.1016/j.patcog.2007.02.007.
(http://www.sciencedirect.com/science/article/pii/S0031320307000945)
Keywords: Microarray; Feature selection; Markov blanket; Genetic algorithm (GA); Memetic algorithm (MA)

---

#摘要

Microarray technologies
the smallest possible set of genes

Markov blanket-embedded genetic algorithm (MBEGA) for gene selection problem

Markov blanket and predictive power in classifier model

filter, wrapper, and standard GA

evaluation criteria:
classification accuracy, number of selected genes, computational cost, and robustness

---

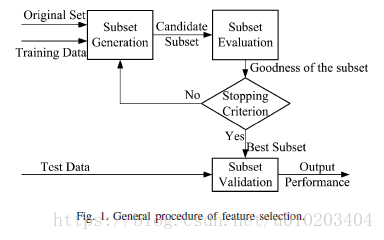
#主要内容

---

##Markov Blanket（Markov毯）

$F$ — 所有特征的集合
$C$ — 类别

一个特征$F_i$的Markov毯 定义如下：

定义（Markov毯）
$M$ — 一个特征子集（不包含$F_i$）
即，$M\in F$且$F_i\notin M$。
$M$为$F_i$的一个Markov毯，若
给定$M$，$F_i$是对于 ( F ∪ C ) − M − { F i } \left( F \cup C \right) - M - \left\{ F_i \right\} (F∪C)−M−{Fi​}条件独立的，
即， P ( F − M − { F i } , C ∣ F i , M ) = P ( F − M − { F i } , C ∣ M ) P \left( F - M - \left\{ F_i \right\}, C | F_i, M \right) = P \left( F - M - \left\{ F_i \right\}, C | M \right) P(F−M−{Fi​},C∣Fi​,M)=P(F−M−{Fi​},C∣M)

给定X，两个属性A与B是条件独立的，若$P \left( A | X, B \right) = P \left( A | X \right) $，也就是说，B并不能在X之外提供关于A的信息。若一个特征$F_i$在当前选择的特征子集中有一个Markov毯$M$，那么$F_i$在$M$之外关于$C$不能提供其他选择的特征的信息，因此，$F_i$能够安全移除。然而，决定特征的条件独立的计算复杂度通常非常高，因此，只使用一个特征来估计$F_i$的Markov毯。

定义（近似Markov毯）
对于两个特征$F_i$与$F_j$ $i̸=j$，$F_j$可看作为$F_i$的近似Markov毯，若$S{U}_{j,C}\ge S{U}_{i,C}$ 且 $S{U}_{i,j}\ge S{U}_{i,C}$，其中，
对称不确定性（symmetrical uncertainty，SU）度量特征（包括类，$C$）间的相关性，定义为：

$IG\left(F_i|F_j\right)$ — 特征$F_i$与$F_j$间的信息增益
$H\left(F_i\right)$与$H\left(F_j\right)$ — 特征$F_i$与$F_j$的熵
$S{U}_{i,C}$ — 特征$F_i$与类$C$间的相关性，称为C-correlation
一个特征被认为是相关的若其C-correlation高于用户给定的阈值$\gamma$，即，$S_{i,C}>\gamma$
没有任何近似Markov毯的特征为predominant feature主导特征

---

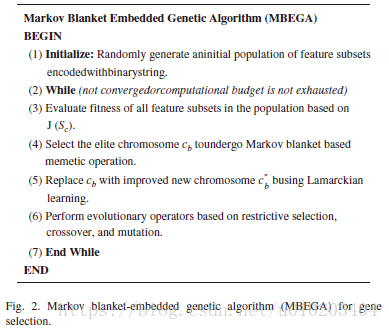
##马尔可夫毯式嵌入式遗传算法

若适应值差异小于$\epsilon$，则特征数较少的个体较好

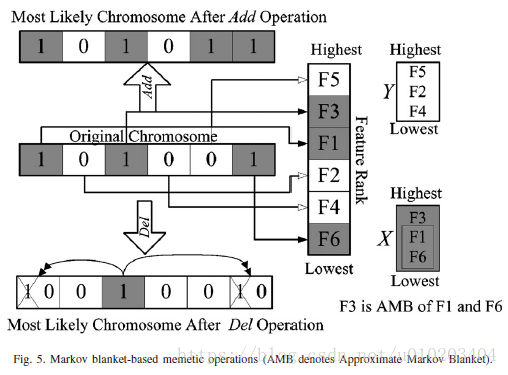
Lamarckian learning：
通过将局部改进的个体放回种群竞争繁殖的机会，来迫使基因型反映改进的效果

$X$ — 选择的特征子集
$Y$ — 排除的特征子集

C-correlation 只计算一次

搜索范围$L$ — 定义了$Add$与$Del$操作的最大数目 — $L^2$个操作组合
随机顺序 — 直到得到改进提升效果

Lamarckian learning process

之后是
usual evolutionary operations：

1. linear ranking selection
2. uniform crossover
3. mutation operators with elitism

---

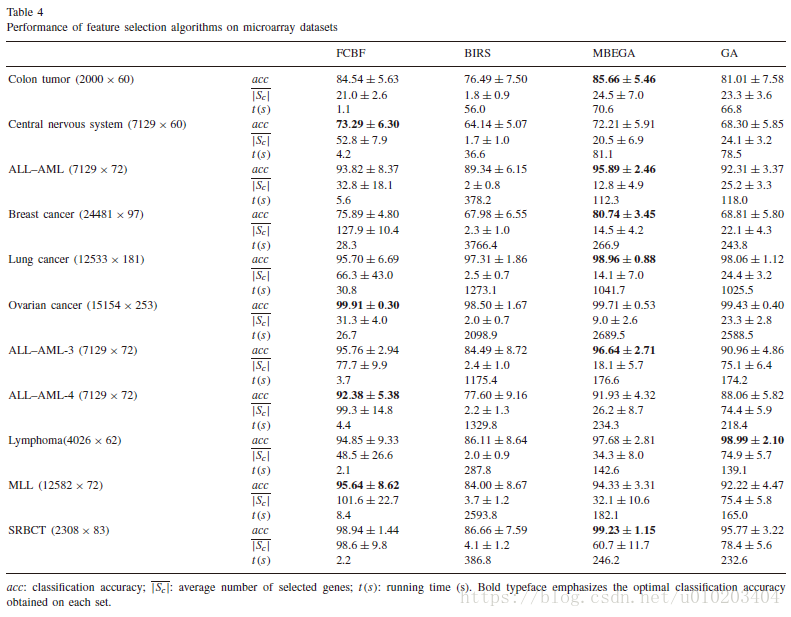
##试验

MBEGA method

考虑了：

1. the FCBF (fast correlation-based filter)
2. BIRS (best incremental ranked subset)
3. standard GA feature selection algorithms

FCBF —
a fast correlation based filter method

1. selecting a subset of relevant features whose C-correlation are larger than a given threshold $\gamma$
2. sorts the relevant features in descending order in terms of C-correlation
3. redundant features are eliminated one-by-one in a descending order

A feature is redundant 仅当 it has an approximate Markov blanket

predominant features with zero redundant features in terms of C-correlation

BIRS — a similar scheme as the FCBF
evaluates the goodness of features using a classifier

1. ranking the genes according to some measure of interest
2. sequentially selects the ranked features one-by-one based on their incremental usefulness

calls to the classifier as many times as the number of features

$BIR{S}_F$ or $BIR{S}_W$ — 基于 — C-correlation (i.e., symmetrical uncertainty between feature $F_i$ and the class $C$) or individual predictive power

$BIR{S}_F$ 耗时更少

---

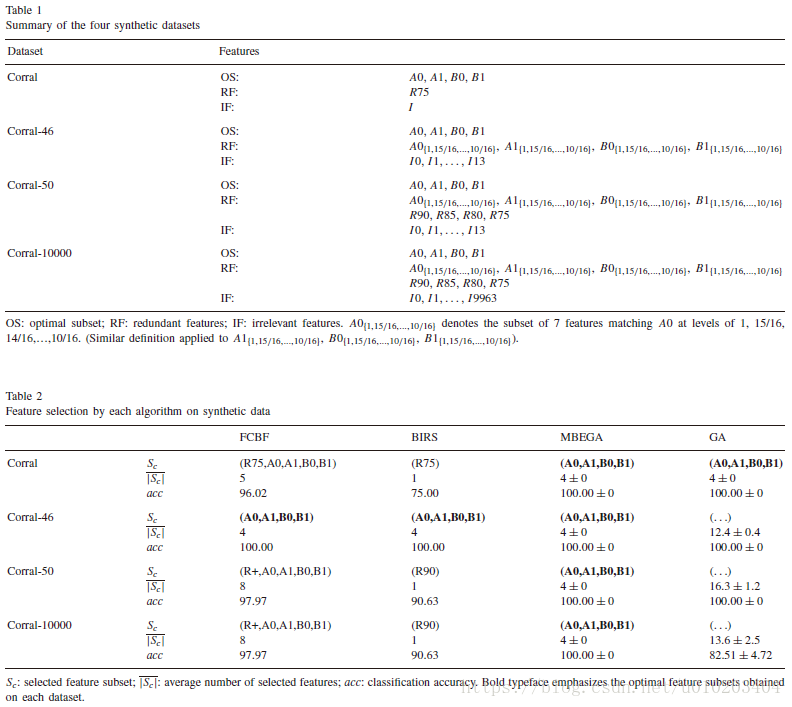
###synthetic data 合成数据

ten 10-fold crossvalidations
with C4.5 classifier

10 independent runs

The maximum number of selected features in each chromosome, m, is set to 50.

---

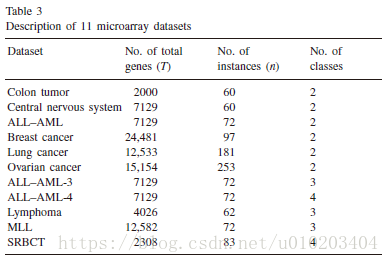
###microarray data 微阵列数据

The .632+ bootstrap

K次重采样

the support vector machine (SVM) — microarray classification problems

one-versus-rest strategy — multi-class datasets

the linear kernel SVM

这篇关于马尔可夫毯式遗传算法在基因选择中的应用的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---