多模态EDA论文小记

本文主要是介绍多模态EDA论文小记，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

论文地址

该论文主要改进点是：通过动态化局部搜索中每个集群大小，高斯和柯西分布共同产生个体。总的来说改进点不多，当然也可能是笔者还没发现。

局部搜索

划分集群

划分集群有两个策略分别是：

• 随机生成一个点作为中心点，将该点半径r内点划为一个集群
• 选择最优个体作为中心点，将该点半径r内点划为一个集群

下图分别是两种划分方式。

这两个方法对于参数都比较敏感，具体来说就是集群大小参数设置将很大程度影响最终结果。例如如果集群大小过于大将导致集群个数少导致对于全局搜索无法兼顾。如果集群大小过于小将无法很好地将结果收敛。

局部搜索

局部搜索的一大作用是提高算法的精度。众所周知EDA在结果精度上有较大不足。因此在每次局部搜索中都使用高斯分布，因为高斯分布具有分布范围较小的特点。为了提高精度，算法需要经可能将分布的范围控制的小，因此此处高斯分布的方差被定义为一个极小的数1.0E-4，
对于每个集群，都有一个核心点也就是适应度最好的点。这个点的个体是作为高斯分布中均值。

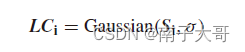
上面公式中LCi作为新生成的个体。如果该个体优于该集群的核心点，就讲核心点替换为该新生成点。

局部概率

为了避免无意义的局部搜索，具体来说就是局部搜索目的是为了提高结果精度。需要在较好的集群中进行搜素即可。而对于那些较差的集群没必要一直进行局部搜索，但是依旧要为那些较差集群一定概率用于局部搜索，这样可以一定程度上避免局部最优。
因此根据上文。需要根据个体适应度建立一个概率模型。得出公式为：
$$\underset{i}{\mathrm{Pr}}=\frac{F_i}{F_{\max }}$$
但是这个公式有个缺点是如果有值适应度为负数将导致没有机会进行局部搜搜，同时还有个问题就是如果$F_{max}$如果为负数将导致错误，因为分母不得为0。因此需要对该公式改进。
首先需要将在分母中加上最小值的绝对值可以解决最小值为0的问题，但是为了保证全局最优个体每次都可以进行局部搜索，需要在分子中也加上最小的适应度。同时为了防止分母为0，还需要将分子分母同时加上一个数，这个数目的是保证分母不为0，因此需要加个极小值，避免对概率公式干扰，修改后结果如下：
$$\underset{i}{\mathrm{Pr}}=\frac{F_i+|F_{\min }|+\xi }{F_{\max }+|F_{\min }|+\xi }$$

高斯和柯西分布交替使用

在每次迭代中，由于高斯分布搜索范围较为狭窄，对于全局搜索能力较差。而柯西分布具有“长尾性”，因此柯西分布对于全局搜索具有一定帮助，为了同时兼顾收敛能力和全局搜索能力，在算法中混合使用。每个分布生成个体都有相同概率。

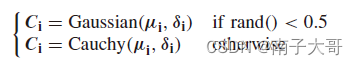
算法

将上述内容结合得到总体算法流程。


这两个图别是利用不同的集群划分算法。区别是集群划分方式不同。

参考资料

https://ieeexplore.ieee.org/abstract/document/7407318

这篇关于多模态EDA论文小记的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---