本文主要是介绍模拟集成电路(2)----MOSFET大小信号分析,二级效应,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
模拟集成电路(2)----MOSFET大小信号分析,二级效应
文章目录
- 模拟集成电路(2)----MOSFET大小信号分析,二级效应
- MOS的结构及符号
- 大信号特性
- Turn-on process for an NMOS
- 耗尽区
- 反形层形成
- I-V特性推导
- 饱和区 ( V D S > V G S − V T H ) (V_{DS}> V_{GS}-V_{TH}) (VDS>VGS−VTH)
- 小信号模型
- MOSFET的跨导
- 小信号模型的物理意义
- 二阶效应
- 体效应( V B ≠ V S V_B \ne V_S VB=VS)
- 体效应对小信号模型的影响
- 沟道长度调制效应
- 对小信号模型电流的影响
- 小信号模型的电阻
- 亚阀值效应
- MOS器件电容
MOS的结构及符号
以NMOS为例
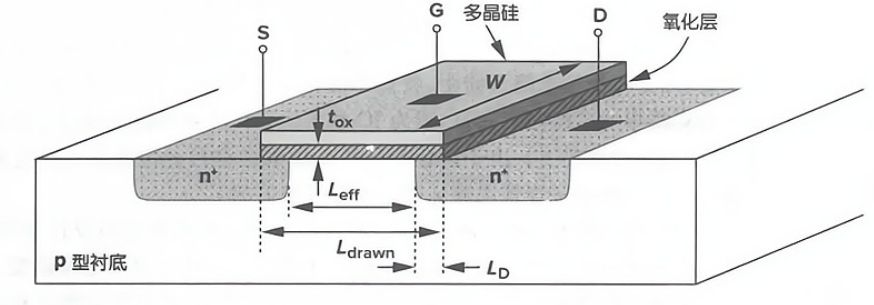

其中,B为body,代表衬底。 V B V_{B} VB代表衬底电压
关于源极和漏极,一般认为电压高的一端为漏极。

MOS管的典型应用
-
开关
-
压控电流源(饱和区)
大信号特性
Turn-on process for an NMOS
假设对栅极施加电压,当这个电压大于一个值 ( V T H ) (V_{TH}) (VTH)时,如MOS管导通,称这个值为阈值电压。阈值电压的定义如下:
V T H = Φ M S + 2 Φ F + Q d e p C o x V_{\mathrm{TH}}=\Phi_{\mathrm{MS}}+2\Phi_{\mathrm{F}}+\frac{Q_{\mathrm{dep}}}{C_{\mathrm{ox}}} VTH=ΦMS+2ΦF+CoxQdep
耗尽区
由于NMOS衬底为P型掺杂,故有大量空穴在电荷周围,当对栅极施加电压不断增加时 ( 限制在 V G S < V T H ) (限制在V_{GS}<V_{TH}) (限制在VGS<VTH),此时有p衬底中的空穴被赶离栅极,形成了一个耗尽层,但由于没有载流子无电流产生,此时MOS还没有导通。

反形层形成
当 ( V G S = V T H ) (V_{GS}=V_{TH}) (VGS=VTH)此时有栅极中空穴浓度等于电子浓度,没有载流子无电流产生。
当 ( V G S > V T H ) (V_{GS}>V_{TH}) (VGS>VTH)此时有栅极中空穴浓度小于电子浓度,电子到达漏端,形成了载流子的通道(反型成)。若此时S端和D端有压差即可产生电流。
I-V特性推导
当反型层形成时,产生的均匀的沟道电荷密度如下:
Q d = W C o x ( V G S − V T H ) Q_\mathrm{d}=WC_\mathrm{ox}(V_\mathrm{GS}-V_\mathrm{TH}) Qd=WCox(VGS−VTH)
三极管区 ( V D S ≤ V G S − V T H ) (V_{DS}\le V_{GS}-V_{TH}) (VDS≤VGS−VTH)
由于D端和S端有压差,所以事实上载流子在栅极的分布并不是均匀的,此时我们看作线性分布,加入了 V ( x ) V(x) V(x)电压和距离为线性分布, V ( x ) = V G S − V T H V(x)=V_{\mathrm{GS}}-V_{\mathrm{TH}} V(x)=VGS−VTH。
此时电流大小与载流子迁移率 μ \mu μ和电场大小 E E E有关(决定了载流子移动速度)
I D = Q d ⋅ v = − W C o x [ V G S − V ( x ) − V T H ] v v = μ E I_{\mathrm{D}}=Q_d·v=-WC_{\mathrm{ox}}[V_{\mathrm{GS}}-V(x)-V_{\mathrm{TH}}]v \\ v=\mu E ID=Qd⋅v=−WCox[VGS−V(x)−VTH]vv=μE
有 V ( 0 ) = 0 和 V ( L ) = V D S V(0)=0\text{ 和 }V(L)=V_{\mathrm{DS}} V(0)=0 和 V(L)=VDS,可得:
∫ x = 0 L I D d x = ∫ V = 0 V D S W C o x μ n [ V G S − V ( x ) − V T H ] d V \int_{x=0}^{L}I_{\mathrm{D}}\mathrm{d}x=\int_{V=0}^{V_{\mathrm{DS}}}WC_{\mathrm{ox}}\mu_{\mathrm{n}}[V_{\mathrm{GS}}-V(x)-V_{\mathrm{TH}}]\mathrm{d}V ∫x=0LIDdx=∫V=0VDSWCoxμn[VGS−V(x)−VTH]dV
化简得:(重要公式)
I D = μ n C o x W L [ ( V G S − V T H ) V D S − 1 2 V D S 2 ] I_{\mathrm{D}}=\mu_{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L}\Big[(V_{\mathrm{GS}}-V_{\mathrm{TH}})V_{\mathrm{DS}}-\frac{1}{2}V_{\mathrm{DS}}^{2}\Big] ID=μnCoxLW[(VGS−VTH)VDS−21VDS2]
可以看作为 V D S V_{DS} VDS关于 V D V_D VD的一个二次函数,其中顶点(最大值为 V D S = V G S − V T H V_{DS}=V_{GS}-V_{TH} VDS=VGS−VTH)

若有 V D S ≪ 2 ( V G S − V T H ) V_{\mathrm{DS}}\ll2\left(V_{\mathrm{GS}}-V_{\mathrm{TH}}\right) VDS≪2(VGS−VTH),可以将这个区域的 V D S V_{DS} VDS- V D V_D VD关系看作是线性的,此区域我们称作深三极管区:
I D ≈ μ n C o x W L ( V G S − V T H ) V D S I_{\mathrm{D}}\approx\mu_{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L}(V_{\mathrm{GS}}-V_{\mathrm{TH}})V_{\mathrm{DS}} ID≈μnCoxLW(VGS−VTH)VDS

此时可以把MOS管看作为一个可控线性电阻。
R o n = 1 μ n C o x W L ( V G S − V T H ) R_{\mathrm{on}}=\frac{1}{\mu_{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L}(V_{\mathrm{GS}}-V_{\mathrm{TH}})} Ron=μnCoxLW(VGS−VTH)1

饱和区 ( V D S > V G S − V T H ) (V_{DS}> V_{GS}-V_{TH}) (VDS>VGS−VTH)
即使此时已经形成了反型层,但由于栅极电压分布并不均匀,在栅极的特定位置会出现 V ( x ) = V G S − V T H V(x)=V_{\mathrm{GS}}-V_{\mathrm{TH}} V(x)=VGS−VTH,形成耗尽区,耗尽区与饱和区相接的点我们称之为夹断点,但是由于电场的存在仍然会产生电流,
I D = 1 2 μ n C o x W L ′ ( V G S − V T H ) 2 I_{\mathrm{D}}=\frac{1}{2}\mu_{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L^{\prime}}(V_{\mathrm{GS}}-V_{\mathrm{TH}})^2 ID=21μnCoxL′W(VGS−VTH)2

对于长沟道的MOS管,我们通常忽略L的变化
I D = 1 2 μ n C o x W L ( V G S − V T H ) 2 I_{\mathrm{D}}=\frac{1}{2}\mu_{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L}(V_{\mathrm{GS}}-V_{\mathrm{TH}})^2 ID=21μnCoxLW(VGS−VTH)2
此时我们可以把MOS管看作为一个压控电流源

小信号模型
MOS管的小信号模型:

V i n = V B + ν i n = V B + ν a sin ( ω t ) V_{in}=V_{B}+\nu_{in}=V_{B}+\nu_{a}\sin(\omega t) Vin=VB+νin=VB+νasin(ωt)
V i n = V B + ν i n = V B + ν a sin ( ω t ) I d = μ n C o x 2 W L ( V i n − V T H ) 2 = μ n C o x 2 W L [ ( V B − V T H ) + ν a sin ( ω t ) ] 2 = I D + [ μ n C o x W L ( V B − V T H ) ] ⋅ ν o sin ( ω t ) + μ n C o x 2 W L ⋅ [ ν a sin ( ω t ) ] 2 \begin{aligned}&V_{in}=V_{B}+\nu_{in}=V_{B}+\nu_{a}\sin(\omega t)\\&I_{d}=\frac{\mu_{n}C_{ox}}{2}\frac{W}{L}(V_{in}-V_{TH})^{2}=\frac{\mu_{n}C_{ox}}{2}\frac{W}{L}[(V_{B}-V_{TH})+\nu_{a}\sin(\omega t)]^{2}\\&=I_{D}+[\mu_{n}C_{ox}\frac{W}{L}(V_{B}-V_{TH})]\cdot\nu_{o}\sin(\omega t)+\boxed{\frac{\mu_{n}C_{ox}}{2}\frac{W}{L}\cdot[\nu_{a}\sin(\omega t)]^{2}}\end{aligned} Vin=VB+νin=VB+νasin(ωt)Id=2μnCoxLW(Vin−VTH)2=2μnCoxLW[(VB−VTH)+νasin(ωt)]2=ID+[μnCoxLW(VB−VTH)]⋅νosin(ωt)+2μnCoxLW⋅[νasin(ωt)]2
框住的一部分为非线性,如果施加的 V a V_a Va很小的话,我们小信号模型即为抛开这部分非线性的部分后进行分析。
I d = I D + i d V o u t = V D D − I d R D = ( V D D − I D R D ) − i d R D = V O U T + v o u t \begin{aligned}I_{d}=I_{D}+i_{d}&V_{out}=V_{DD}-I_{d}R_{D}=(V_{DD}-I_{D}R_{D})-\boxed {i_{d} R_{D} } \\&=V_{OUT}+\boxed{v_{out}}\end{aligned} Id=ID+idVout=VDD−IdRD=(VDD−IDRD)−idRD=VOUT+vout
ν o u t = − i d R D = − μ n C o x W L ( V B − V T H ) ⋅ R D ⋅ v a sin ( ω t ) \nu_{out}=-i_{d}R_{D}=-\boxed{ \mu_{n}C_{ox}\frac{W}{L}(V_{_B}-V_{_{TH}})\cdot R_{_D}}\cdot v_{_a}\sin(\omega t) νout=−idRD=−μnCoxLW(VB−VTH)⋅RD⋅vasin(ωt)
ν i n → Convert to current g m i d → Back to voltage R D ν o u t = − g m ν i n R D \nu_{in}\xrightarrow[\text{Convert to current}]{g_m}i_d\xrightarrow[\text{Back to voltage}]{R_D}\nu_{out=}-g_m\nu_{in}R_D νingmConvert to currentidRDBack to voltageνout=−gmνinRD
全部用小写:只考虑了微小变化,所以有跨导的话就可以拿来就用。

MOSFET的跨导
由于MOSFET工作在饱和区时,其电流受栅源过驱动电压控制,跨导即表示电压转换电流的能力。
g m = ∂ I D ∂ V G S ∣ V D S , c o n s t = μ n C o x W L ( V G S − V T H ) \begin{aligned}g_{\mathrm{m}}&=\left.\frac{\partial I_{\mathrm{D}}}{\partial V_{\mathrm{GS}}}\right|_{V_{\mathrm{DS}},\mathrm{const}}\\&=\mu_{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L}(V_{\mathrm{GS}}-V_{\mathrm{TH}})\end{aligned} gm=∂VGS∂ID VDS,const=μnCoxLW(VGS−VTH)
g m = 2 μ n C o x W L I D = 2 I D V G S − V T H \begin{gathered} {g_m} =\sqrt{2\mu_{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L}I_{\mathrm{D}}} \\ =\frac{2I_\mathrm{D}}{V_\mathrm{GS}-V_\mathrm{TH}} \end{gathered} gm=2μnCoxLWID=VGS−VTH2ID

例如:

g m = ∂ ∂ V G S { 1 2 μ n C o x W L [ 2 ( V G S − V T H ) V D S − V D S 2 ] } = μ n C o x W L V D S \begin{aligned} g_m & =\frac{\partial}{\partial V_{\mathrm{GS}}}\left\{\frac{1}{2}\mu_{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L}\Big[2(V_{\mathrm{GS}}-V_{\mathrm{TH}})V_{\mathrm{DS}}-V_{\mathrm{DS}}^{2}\Big]\right\} \\ &=\mu_{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L}V_{\mathrm{DS}} \end{aligned} gm=∂VGS∂{21μnCoxLW[2(VGS−VTH)VDS−VDS2]}=μnCoxLWVDS
如果器件进入三极管区,跨导将下降。因此,放大应用时,我们通常使MOSFET工作于饱和区。
小信号模型的物理意义
实际上就是一个泰勒展开的过程,到一个偏执点,给出电压电流关系,把高阶部分去掉只留下线性部分。
把不理想的东西去掉,将非线性线性化。
二阶效应
体效应( V B ≠ V S V_B \ne V_S VB=VS)
随着 V B < 0 V_B<0 VB<0耗尽层变得更宽了,由此 V T H V_{TH} VTH也提高了。
若 V B = 0 , V S > 0 V_B=0,V_S>0 VB=0,VS>0也是同样的效果,仍会出现体效应。


如上图有:
V o u t = V i n − V G S V_{out}=V_{in}-V_{GS} Vout=Vin−VGS
V G S = 2 I D μ n C o x W L + V T H \begin{gathered} V_{GS}=\sqrt{\frac{2I_D}{\mu_{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L}}} +V_{TH} \end{gathered} VGS=μnCoxLW2ID+VTH
如果不考虑体效应就是图b, V T H V_{TH} VTH没有变化,即为 V G S V_{GS} VGS没有改变。
如果不考虑体效应就是图c, V T H V_{TH} VTH变化, V G S V_{GS} VGS改变。
体效应对小信号模型的影响
有体跨导和栅跨导 g m b g_{mb} gmb。
g m b = ∂ I D ∂ V B S = μ n C o x W ˙ L ( V G S − V T H ) ( − ∂ V T H ∂ V B S ) \begin{aligned} g_{mb} & =\frac{\partial I_{\mathrm{D}}}{\partial V_{\mathrm{BS}}} \\ &=\mu_{\mathrm{n}}C_{\mathrm{ox}}\frac{\dot{W}}{L}(V_{\mathrm{GS}}-V_{\mathrm{TH}})(-\frac{\partial V_{\mathrm{TH}}}{\partial V_{\mathrm{BS}}}) \end{aligned} gmb=∂VBS∂ID=μnCoxLW˙(VGS−VTH)(−∂VBS∂VTH)
又有:
∂ V T H ∂ V B S = − ∂ V T H ∂ V S B = − γ 2 ( 2 Φ F + V S B ) − 1 2 \begin{aligned}\frac{\partial V_{\mathrm{TH}}}{\partial V_{\mathrm{BS}}}&=-\frac{\partial V_{\mathrm{TH}}}{\partial V_{\mathrm{SB}}}\\&=-\frac{\gamma}{2}(2\Phi_{F}+V_{\mathrm{SB}})^{-\frac{1}{2}}\end{aligned} ∂VBS∂VTH=−∂VSB∂VTH=−2γ(2ΦF+VSB)−21
可得重要公式:
g m b = g m γ 2 2 Φ F + V S B = η g m \begin{aligned}g_{\mathrm{mb}}&=g_{\mathrm{m}}\frac{\gamma}{2\sqrt{2\Phi_{\mathrm{F}}+V_{\mathrm{SB}}}}\\&=\eta g_{\mathrm{m}}\end{aligned} gmb=gm22ΦF+VSBγ=ηgm
看是通过体效应还是栅效应来控制电流。其影响因素并不一样。

沟道长度调制效应
理想电流源的条件:NMOS工作在饱和区,且沟道长度足够长。
假设沟道长度不够长, L ′ L' L′为夹断产生的耗尽区长度:
L ′ = L − Δ L L'=L-\Delta L L′=L−ΔL
如果x足够小有 1 1 − x = 1 1 + x \frac{1}{1-x}=\frac{1}{1+x} 1−x1=1+x1
1 L ′ = 1 L − Δ L = 1 L 1 ( 1 − Δ L / L ) ≈ 1 L ( 1 + Δ L L ) \frac1{L^{\prime}}=\frac1{L-\Delta L}=\frac1L\frac1{(1-\Delta L/L)}\approx\frac1L(1+\frac{\Delta L}L) L′1=L−ΔL1=L1(1−ΔL/L)1≈L1(1+LΔL)
a s s u m e Δ L / L = λ V D S , 1 / L ′ = 1 L ( 1 + λ V D S ) assume\Delta L/L=\lambda V_{DS},1/L^{\prime}=\frac{1}{L}(1+\lambda V_{DS}) assumeΔL/L=λVDS,1/L′=L1(1+λVDS)
λ \lambda λ是沟道长度调制系数:

λ = 1 L ( Δ L V D S ) ∝ 1 L \lambda=\frac1L(\frac{\Delta L}{V_{DS}})\propto\frac1L λ=L1(VDSΔL)∝L1
V A + V D S 1 V D S 2 − V D S 1 = I D 1 I D 2 − I D 1 λ = 1 V A = I D 2 − I D 1 I D 1 V D S 2 − I D 2 V D S 1 \begin{gathered}\frac{V_{A}+V_{DS1}}{V_{DS2}-V_{DS1}}=\frac{I_{D1}}{I_{D2}-I_{D1}} \\\lambda=\frac{1}{V_{A}}=\frac{I_{D2}-I_{D1}}{I_{D1}V_{DS2}-I_{D2}V_{DS1}} \end{gathered} VDS2−VDS1VA+VDS1=ID2−ID1ID1λ=VA1=ID1VDS2−ID2VDS1ID2−ID1
I D ≈ 1 2 μ n C o x W L ( V G S − V T H ) 2 ( 1 + λ V D S ) I_{\mathrm{D}}\approx\frac{1}{2}\mu_{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L}(V_{\mathrm{GS}}-V_{\mathrm{TH}})^{2}(1+\lambda V_{\mathrm{DS}}) ID≈21μnCoxLW(VGS−VTH)2(1+λVDS)
其与L的长度和工艺有关。
对小信号模型电流的影响
I D I_D ID受 V D S V_{DS} VDS的变化是非线性的.
I D = μ n C O X 2 W L ( V G S − V T H ) 2 ( 1 + λ V D S ) I_D=\frac{\mu_nC_{OX}}2\frac WL(V_{GS}-V_{TH})^2(1+\lambda V_{DS}) ID=2μnCOXLW(VGS−VTH)2(1+λVDS)
可以把其影响看作为一个电阻。
小信号模型的电阻
r o = ∂ V D S ∂ I D = 1 ∂ I D / ∂ V D S = 1 1 2 μ n C o x W L ( V G S − V T H ) 2 λ ≈ 1 + λ V D S λ I D ≈ 1 λ I D \begin{aligned} r_o& =\frac{\partial V_{\mathrm{DS}}}{\partial I_{\mathrm{D}}} \\ &=\frac1{\partial I_\mathrm{D}/\partial V_\mathrm{DS}} \\ &=\frac{1}{\frac{1}{2}\mu_{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L}(V_{\mathrm{GS}}-V_{\mathrm{TH}})^{2}\lambda} \\ &\approx\frac{1+\lambda V_{\mathrm{DS}}}{\lambda I_{\mathrm{D}}} \\ &\approx\frac{1}{\lambda I_{\mathrm{~D}}} \end{aligned} ro=∂ID∂VDS=∂ID/∂VDS1=21μnCoxLW(VGS−VTH)2λ1≈λID1+λVDS≈λI D1

漏电压如何受其他三端影响。
亚阀值效应
当 V G S < V T H V_{GS}<V_{TH} VGS<VTH,其实此时电流并不为0.
I D = I 0 exp V G S ζ V T I_{\mathrm{D}}=I_{0}\exp\frac{V_{\mathrm{GS}}}{\zeta V_{T}} ID=I0expζVTVGS
- 低功耗
- 噪声大
- 速度慢
MOS器件电容
一共有两种电容
-
介质电容
-
结电容(包含耗尽层)
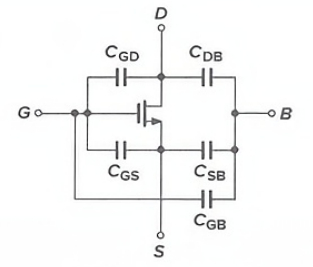

通常我们只考虑 C G S C_{GS} CGS和 C G D C_{GD} CGD
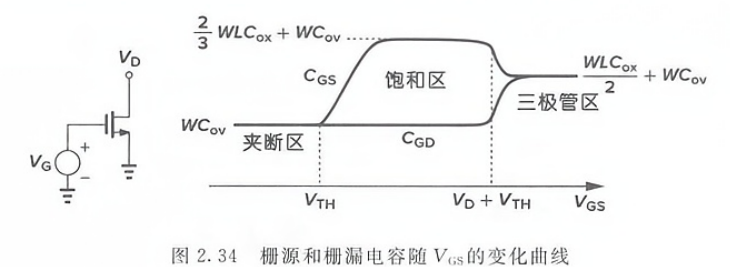
这篇关于模拟集成电路(2)----MOSFET大小信号分析,二级效应的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





