神经网络的认识（二）深层神经网络

本文主要是介绍神经网络的认识（二）深层神经网络，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

深层神经网络

- 深度学习与深层神经网络
- - 非线性激活函数
  - 多层网络
- 损失函数
- - 经典损失函数
- 神经网络优化算法
- 神经网络进一步优化
- - 学习率
  - 过拟合
  - 滑动平均模型

深层学习有两个非常重要的特性———多层和非线性
线性模型的局限性，就是任意线性模型的组合仍然还是线性模型。所以引出激活函数，经过激活函数变换完的输出就不再是线性的了。

深度学习与深层神经网络

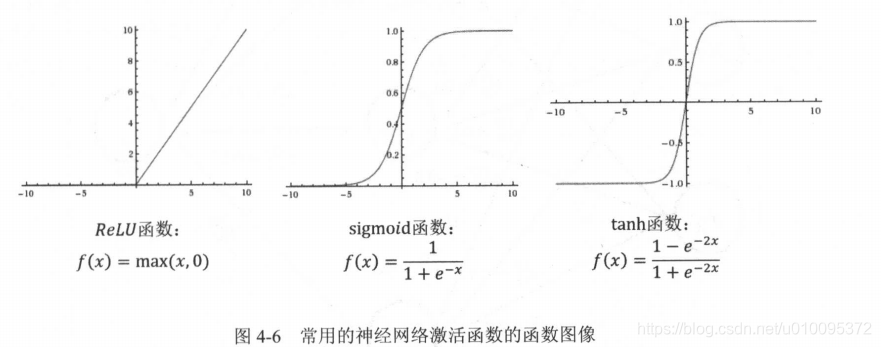
非线性激活函数

如果将每一个神经元（也就是神经网络中的节点）的输出通过一个非线性函数，那么整个神经网络的模型也就不再是线性的了。这个非线性函数就是激活函数。那么整个神经网络的模型也就不再是线性的了。
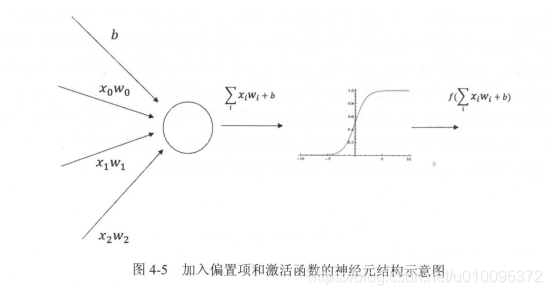
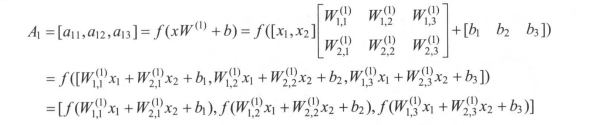
在这里插入图片描述

相对于前面的简单加权和有两个改变

新的公式中增加了偏置项（ bias ），偏置项是神经网络中非常常用的一种结构。
每个节点的取值不再是单纯的加权和。每个节点的输出在加权和的基础上还做了一个非线性变换。

偏置项可以被表达为一个输出永远为 1 的节点。以下公式给出了这个新的神经网络模型前向传播算法的计算方法。
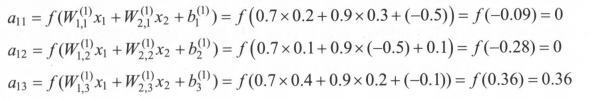
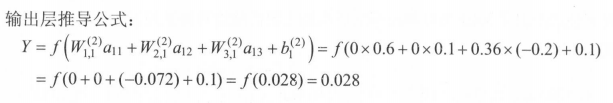
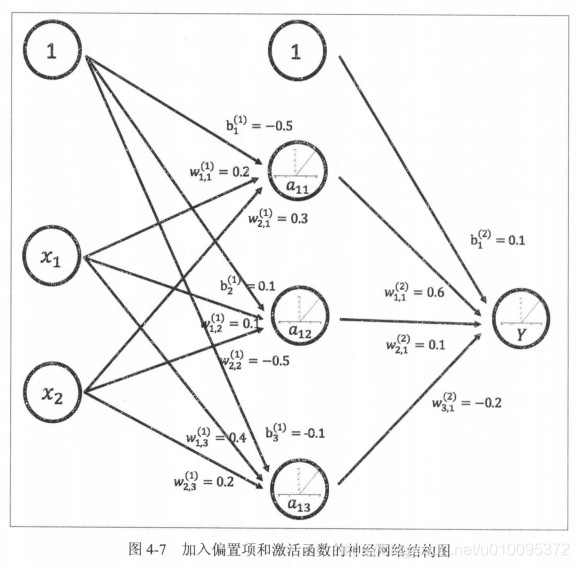
在这里插入图片描述

多层网络

感知机可以简单地理解为单层的神经网络，感知机会先将输入进行加权和，然后再通过激活函数最后得到输出。这个结构就是一个没有隐藏层的神经网络。当加入隐藏层之后，异或问题就可以得到很好地解决。深层神经网络实际上有组合特征提取的功能。这个特性对于解决不易提取特征向量的问题（比如图片识别、语音识别等）有很大帮助。这也是深度学习在这些问题上更加容易取得突破性进展的原因。

输入特征中抽取的更高维的特征

说实话，这里我理解是根据低维的特征能够取到更加深入事务特质的东西

损失函数

我的理解 用损失函数可以理解到预测的值和真实的值之间的差距，因为隐藏层的参数是可以不断优化的，每次优化与否的依据就是损失函数。

经典损失函数

交叉熵交叉熵刻画的是两个概率分布之间的距离，然而神经网络的输出却不一定是一个概率分布。

Softmax 回归本身可以作为一个学习算法来优化分类结果，将神经网络前向传播得到的结果变成概率分布。
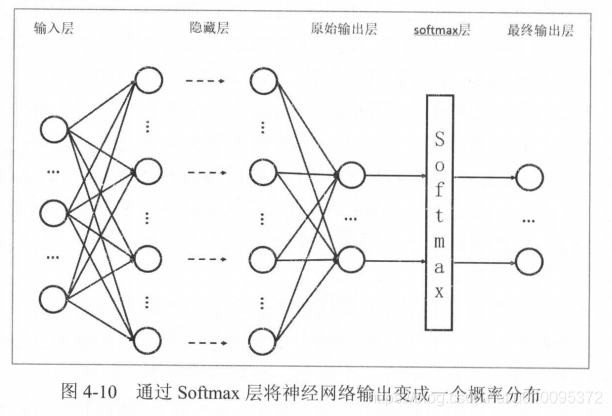
在这里插入图片描述
原始神经网络的输出被用作置信度来生成新的输出，而新的输出满足概率分布的所有要求。

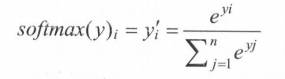
举个例子
三分类问题，某个样例的正确答案是（1，0，0 ）。某模型经过 Softmax 回归之后的预测答案是（ 0.5 ,0.4,0.1 ），那么这个预测和正确答案之间的交叉熵为
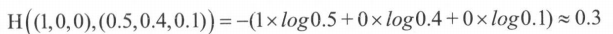
在这里插入图片描述
如果另外一个模型的预测是（0.8, 0.1, 0.1 ），那么这个预测值和真实值之间的交叉熵是：

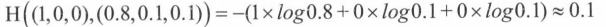
交叉熵一般会与 softmax 回归一起使用，合起来是损失函数。

我理解就是softmax能将输出变成概率分布，然后用交叉熵来计算预测的概率分布跟真实的概率分布有什么关系，所以只能解决分类问题

回归问题解决的是对具体数值的预测
这些问题需要预测的不是一个事先定义好的类别，而是一个任意实数。解决回归问题的神经网络一般只有一个输出节点，这个节点的输出值就是预测值.损失函数就用均方误差：
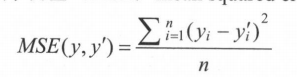
在这里插入图片描述

神经网络优化算法

梯度下降算法主要用于优化单个参数的取值，而反向传播算法给出了一个高效的方式在所有参数上使用梯度下降算法，从而使神经网络模型在训练数据上的损失函数尽可能小。反向传播算法是训练神经网络的核心算法，它可以根据定义好的损失函数优化神经网络中参数的取值，从而使神经网络模型在训练数据集上的损失函数达到一个较小值。

梯度下降算法和反向传播算法

我的理解 前面有了预测值跟真实值的判断依据，那么我就可以填不同的参数值来得出不同的预测值，从中选一个和真实值最相近的。

用 θ 表示神经网络中的参数， J（θ）表示在给定的参数取值下，训练数据集上损失函数的大小，那么整个优化过程可以抽象为寻找一个参数 θ ，使得 J（θ）最小。弄了半天就相当于求J（θ）最小值的时候，参数 θ的值。其实最主要的还是求参数 θ的值。

求得话可以直接找到J（θ）的导数为零，然后求个极大值极小值，可是 J（θ）我们现在还不知道，所以就只能用梯度下降，走一点是一点，自觉地 J（θ）和0特别相近了就到此为止。梯度下降算法会法代式更新参数 θ ，不断沿着梯度
的反方向让参数朝着总损失更小的方向更新。

梯度下降解释

神经网络的优化过程可以分为两个阶段，

通过前向传播算法计算得到预测值，井将预测值和真实值做对比得出两者之间的差距。
通过反向传播算法计算损失函数对每一个参数的梯度，再根据梯度和学习率使用梯度下降算法更新每一个参数。

由于梯度下降耗费时间多，所以有了随机梯度下降算法

随机梯度下降算法每次优化的只是某一条数据上的损失函数，所以它的问题也非常明显：在某一条数据上损失函数更小并不代表在全部数据上损失函数更小，于是使用随机梯度下降优化得到的神经网络甚至可能无法达到局部最优。

实际应用中一般采用这两个算法的折中一一每次计算一小部分训练数据的损失函数。（不是全部也不是某一条，比全部少且比某一条多）

反向传播的解释

神经网络进一步优化

学习率

学习率设的大了，可能把好的结果给略过了，设的小了就可能耗费特别多的时间。于是可以用指数衰减的方法设置梯度下降算法中的学习率。

举个不恰当的例子：就跟摆锤一样，摆锤由于空气阻力，摆动的幅度会越来越小，我们的这个学习率就跟摆锤划过的距离一样，到后面会越来越小，是动态的。

通过这个函数，可以先使用较大的学习率来快速得到一个比较优的解，然后随着迭代的继续逐步减小学习率，使得模型在训练后期更加稳定。

过拟合

在训练的时候，过分以为训练数据是最终目的，而导致在真实的数据上发挥不了效果。所以损失函数也不是越小越好。
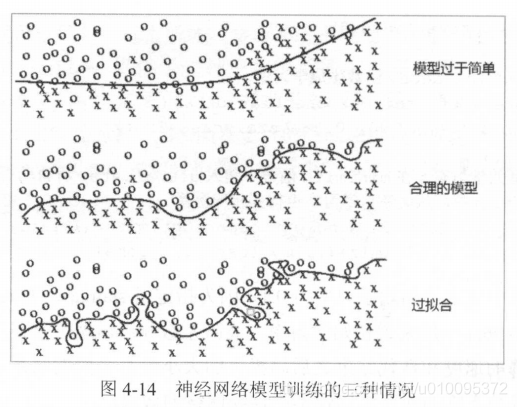
在这里插入图片描述
为了解决过拟合，所以提出了正则化
大神的理解很到位
知乎大神
这个我的理解是由于公式里的参数比如x1, x2, x3, x4…太多了，导致公式对应图出来就是精确的曲曲折折，过拟合了，我们就要想个办法将这些个参数去一去，一般对应的公式就是F(X) = w1*x1 + w2*x2 + w3*x3 + ... + b ，最直接的办法就是想办法将w1，w2，w3 … 这些个权重参数变成0，前面说过的损失函数有计算方差的，那这个防止过拟合措施就是损失函数变成平方差加上正则化，平方差是正数，正则化出来也是正数，损失函数要趋于0，那么平方差要趋于0，正则化也要趋于0，正则化公式是w1² + w2² + … + wn² ，这个式子要趋于0，只能是每个权重参数趋于0，这就变相的实现了将x1, x2, x3, x4 … xn 去掉了。