MATLAB实现遗传算法优化第三类生产线平衡问题

本文主要是介绍MATLAB实现遗传算法优化第三类生产线平衡问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第三类生产线平衡问题的数学模型

假设：

工作站数量（m）和生产线节拍（CT）是预设并固定的。
每个任务（或作业元素）只能分配到一个工作站中。
任务的执行顺序是预先确定的，且不可更改。
每个任务的作业时间是已知的，且不会因为分配到不同的工作站而改变。
不考虑工作站之间的物料搬运时间和等待时间。

变量说明：

n：工序的数量
i：工序的索引，i = 1, 2, ..., n
$t_i$ ：任务 i 的作业时间
m：工作站的数量
CT：生产线的节拍时间
$x_{ij}$ ：二进制变量，如果任务 i 被分配到工作站 j，则 $x_{ij}$ = 1；否则， $x_{ij}$ = 0
$S_{j}$ ：工作站 j 的总作业时间
$Pr_{ik}$ ：二进制变量，如果工序i是工序j的紧前工序,则 $Pr_{ik}$ =1 ；否则， $Pr_{ik}$ =0

目标函数：

平衡率（Balance Rate, BR）是评估生产线平衡效果的重要指标，其计算公式为：

$\text{Maximize } P=\frac{\sum_{j=1}^{m}S_j}{CT\times m}$

其中， $S_j$ 是工作站 j 的总作业时间，计算公式为：

$S_j = \sum_{i=1}^{n} t_i \times x_{ij}$

约束条件：

(1)每个任务只能分配到一个工作站：

$\sum_{j=1}^{m} x_{ij} = 1, \forall i \in {1, 2, ..., n}$

(2)工作站的总作业时间不能超过生产线的节拍时间：

$S_j \leq CT, \forall j \in {1, 2, ..., m}$

(3)作业顺序约束（确保任务按照预定的顺序进行）：

若 $Pr_{ik}$ =1, 则

$\sum_{j=1}^{m} j \times x_{ij} \leq \sum_{j=1}^{m} j \times x_{kj}, \forall i, k$ 这个约束确保了任务之间的先后顺序得到遵守。

遗传算法的流程已经有很多了, 我们不再赘述.

下面我们结合一个20个工序的小算例来用MATLAB实现遗传算法优化第三类生产线平衡问题:

紧前关系:

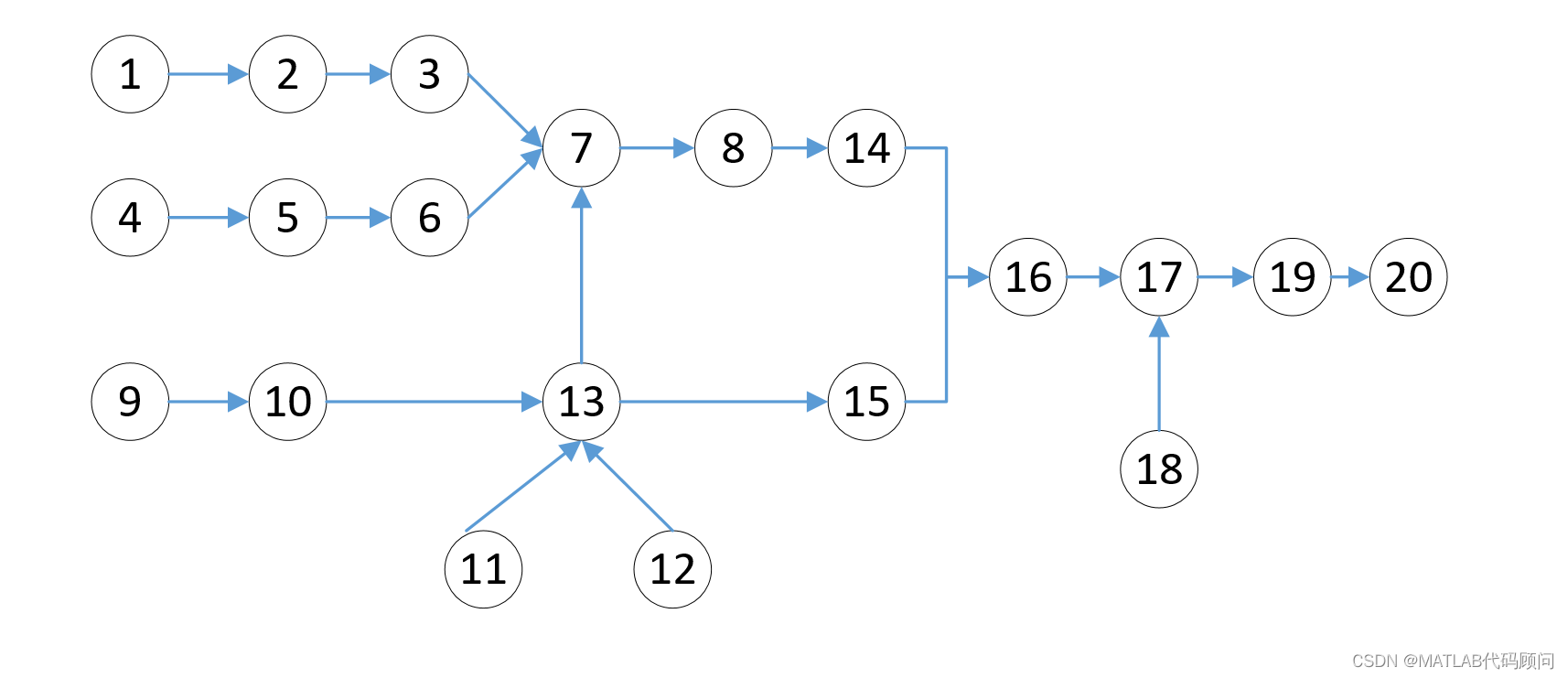
数据:

工序	紧前工序	工作时间(min)
1	0	20
2	1	10
3	2	23
4	0	24
5	4	20
6	6	22
7	3、6	21
8	7	16
9	0	20
10	9	12
11	0	21
12	0	10
13	10、11、12	14
14	8	10
15	13	11
16	14、15	23
17	16	21
18	0	15
19	17	25
20	19	10

工作站设定为4, 节拍为95, 求最大化平衡率, 部分MATLAB主程序如下:

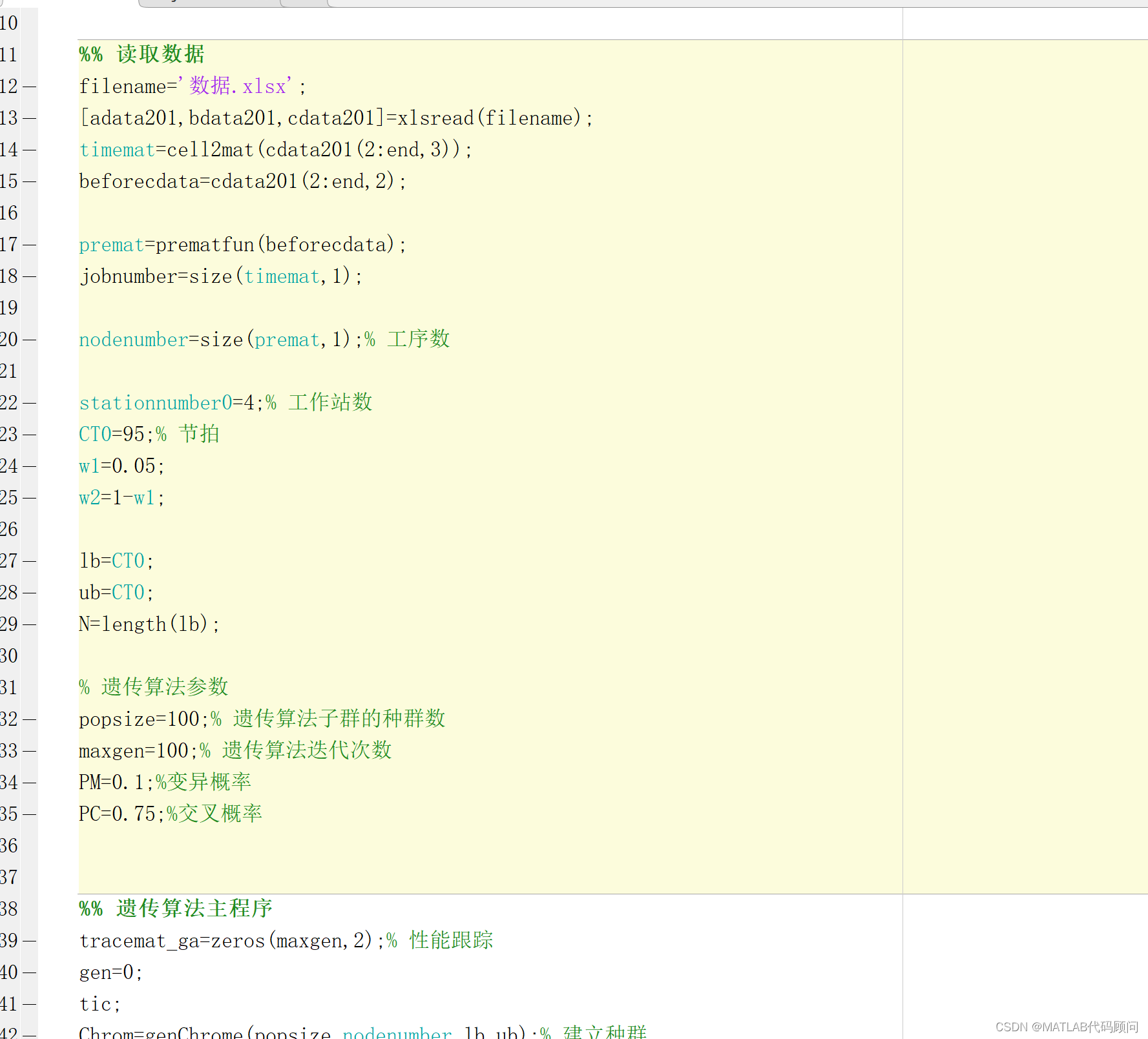
程序结果如下:

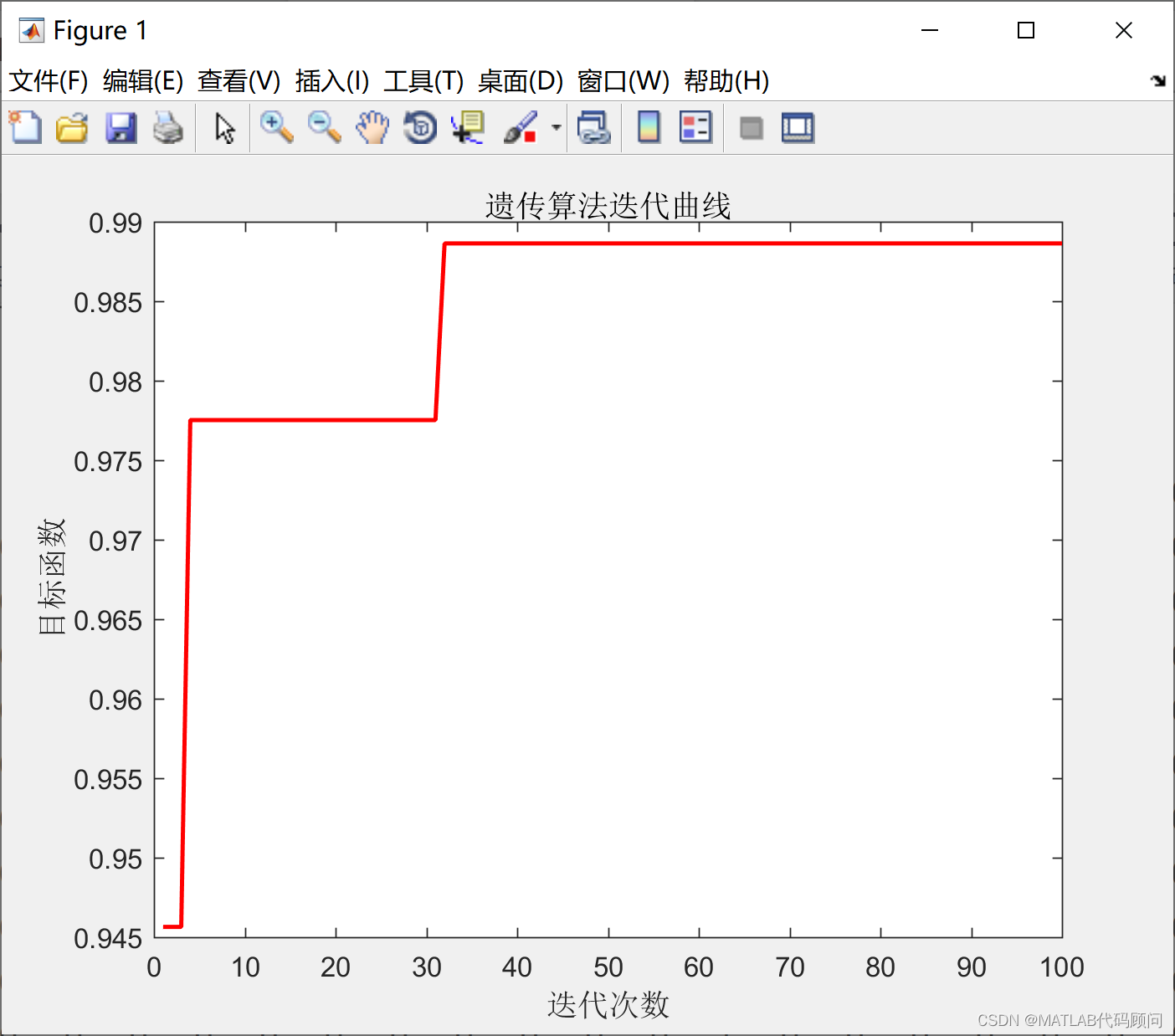
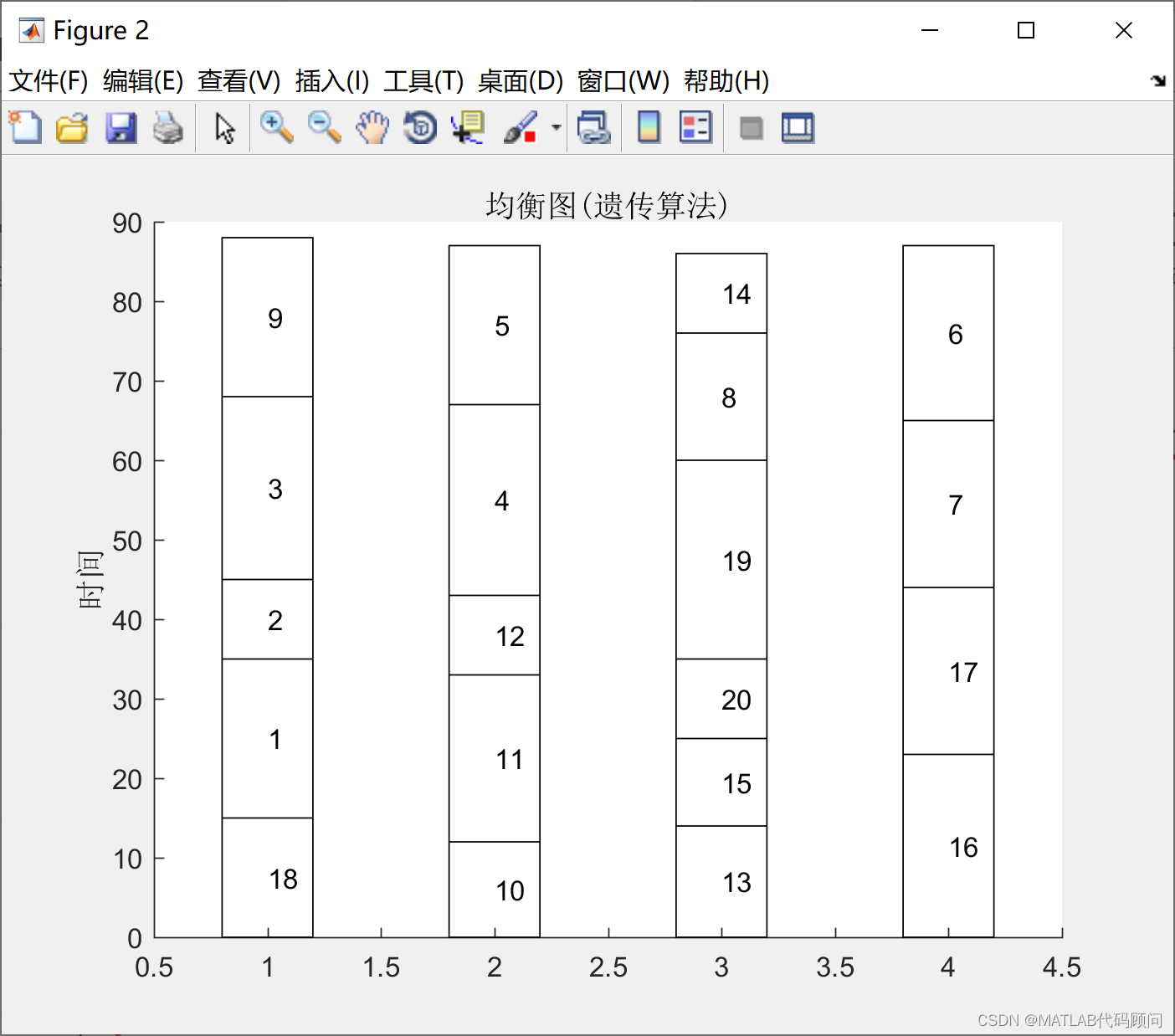
算法运行时间

runtime1 =

23.9561303

遗传算法优化得到的最优目标函数值

bestValue_ga =

1.01149425287356

遗传算法优化得到的最优染色体

bestChrom_ga =

3 5 6 18 7 16 1 2 9 10 11 12 17 4 14 13 15 8 19 20 95

工作站数量

stationnumber =

节拍

CT =

平滑指数

SI =

1.22474487139159

平衡率

P =

0.988636363636364

>> 紧前关系矩阵 premat

premat =

0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0