大语言模型中的第一性原理：Scaling laws

本文主要是介绍大语言模型中的第一性原理：Scaling laws，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

大语言模型的尺度定律在大语言模型的训练过程中起到了非常重要的作用。即使读者不参与大语言模型的训练过程，但了解大语言模型的尺度定律仍然是很重要的，因为它能帮助我们更好的理解未来大语言模型的发展路径。

1. 什么是尺度定律

尺度定律（Scaling laws）是一种描述系统随着规模的变化而发生的规律性变化的数学表达。这些规律通常表现为一些可测量的特征随着系统大小的增加而呈现出一种固定的比例关系。尺度定律在不同学科领域中都有广泛的应用，包括物理学、生物学、经济学等。

有趣的是，OpenAI的研究者在2020年发现，大语言模型也遵循着尺度定律[1]。

大语言模型的尺度定律描述的是模型的性能 𝐿 ，模型的参数量大小 𝑁 ，训练模型的数据大小 𝐷 以及训练模型使用的计算量 𝐶 之间的关系。需要注意的是，这里的尺度定律默认要求大语言模型使用的是Transformer的解码器结构。

模型的性能 𝐿 是指模型在测试集上的交叉熵损失：

            (1)

𝐷 表示token字典表， 𝑇 表示文本样本被划分为token后的长度。值得注意的是，这里的数学表达进行了一定的简化，仅针对单个文本样本。实际上，测试集由多个文本样本组成。

模型的参数量大小 𝑁 是除了静态编码矩阵和位置编码外的参数。

训练数据大小 𝐷 指的是在训练过程中使用的token数量。通常情况下， 𝐷 等于 𝐵𝑆 ，其中 𝐵 代表使用梯度下降法时的批量大小（Batch Size）， 𝑆 表示参数迭代的次数（Step）。

训练模型使用的计算量 𝐶 是指训练模型时，使用的浮点运算次数。每训练一个token会涉及一次前向传播，一次反向传播，在大语言模型的训练中，反向传播的浮点运算次数约为前向传播的两倍。需要注意的是，和参数量大小 𝑁 类似，这里的浮点运算次数需要排除掉静态编码和位置编码。

在使用Transformer的解码器结构训练模型时，我们可以得到如下的关于 𝐶,𝑁,𝐷 之间的近似计算关系：

    (2)

关于上述公式的推导过程，可参考论文“Scaling Laws for Neural Language Models”的2.1小节，在此不再详述。公式(2)表明，当 𝐶 、 𝑁 、 𝐷 三者中已知其中的两个值时，我们可利用上述公式估算出第三个值。

尺度定律的核心结论可以用下面这句话简单总结：

对于计算量 𝐶 ，模型参数量 𝑁 和数据集大小 𝐷 ，当不受其他两个因素制约时，模型性能 𝐿 与每个因素都呈现 幂律关系。

首先，我们来了解一下什么是幂律关系。幂律关系是指类似于如下的数学表达式：

           (3)

这里的 𝑥 是变量， 𝑐,𝛼 是常数。随着 𝑥 的增加， 𝐿(𝑥) 不断减少。有时，我们也会将上式中的 𝑥 替换为，然后两边取对数，将 log⁡𝐿(𝑥) 替换为 𝑦′ ，公式(3)会转换为下面的样子：

𝑦′=𝛼log⁡𝑐−𝛼𝑥′          (4)

公式(4)告诉我们，在幂律关系中，经过适当的变形，可以自然的转换为线性关系。

需要注意的是，大语言模型的尺度定律并非源于理论推导，而是基于经验性的实验分析。那么，尺度定律究竟有何作用呢？至少有以下几个方面：

1. 预测模型效果，便于调整训练策略和超参数。 大语言模型的训练需要大量时间和计算资源。与传统机器学习不同，我们无法直接在大模型和大数据集上进行实验以验证超参数或训练策略。因此，一个明智的做法是在小模型和小数据集上进行训练，然后利用尺度定律将训练效果外推到大模型和大数据集上。通过这种方式，我们可以快速地迭代模型的训练策略和超参数。
2. 合理的分配资源。 训练大语言模型既费时又耗费计算资源。根据尺度定律，我们能够合理地分配模型参数 𝑁 和训练数据大小 𝐷 ，以在有限的预算内尽可能获得效果优良的模型。
3. 分析大语言模型的极限。 通过尺度定律，我们可以尝试分析预训练模型的极限在哪里。

接下来，我们将对尺度定律的一些性质进行更详细的解读。

2. 尺度定律的性质

2.1 三个幂律关系

D与L的幂律关系

限制训练数据大小，在比较大的语言模型上训练，使用早停策略选择停止训练的时机（一旦测试集损失停止下降就停止训练）。换句话说，我们只限制了数据集大小 𝐷，模型参数量 𝑁 和计算量 𝐶 没有被限制。模型性能 𝐿 和 𝐷 有如下的幂律关系：

      (5)

𝐷𝑐 和 𝛼𝐷 均为常数。

为什么公式(5)成立呢？虽然这个公式只是通过数据得到的经验性结论，但我们可以通过一个简单的均值估计模型更深刻地理解幂律关系的内涵。

假设有样本采样自高斯分布。我们用样本均值估计高斯分布的期望 𝜇 。样本均值的定义如下：

   (6)

根据相关的统计学知识，下面的等式成立：

  (7)

公式(7)的左边类似于 𝐿(𝐷) ，度量的是预测值和真实值之间的差异。不难看到公式(7)其实就是一种幂律关系，不同点在于公式(7)中的 𝛼𝐷 为数字 1 。论文"Explaining Neural Scaling Laws"的作者[2]认为，幂律关系中的 1𝛼𝐷 代表数据集“内在的维度”。

N与L的幂律关系

在不限制数据集的情况下，训练具有不同参数量的大语言模型，直至测试集损失达到收敛。换句话说，我们只限制了模型参数量 𝑁 ，而数据集 𝐷 和计算量 𝐶 没有受到限制。模型性能 𝐿 和 𝑁 之间存在如下的幂律关系：

    (8)

𝑁𝑐 和 𝛼𝑁 均为常数。需要注意的是，模型参数量 𝑁 不包含静态编码的矩阵 𝑊𝑒𝑚𝑏 。

C与L的幂律关系

在计算量 𝐶 受限的情况下，通过关系式 𝐶≈6𝑁𝐵𝑆 ，我们可以遍历不同参数量大小的模型，参数学习迭代次后停止。在这个过程中，我们保持批量大小 𝐵 不变。然后，我们可以选择效果最好的一个模型。接着，我们就得到了模型性能 𝐿 和 𝐶 之间的幂律关系：

(9)

均为常数。

需要注意的是，由于这里的批量大小 𝐵 对于所有的模型都是固定不变的。因此上述的经验性结论并不是最优的结论。在论文“Scaling Laws for Neural Language Models”中，作者进一步定义了 𝐶𝑚𝑖𝑛 ，并总结了 𝐶𝑚𝑖𝑛 和模型性能 𝐿 的幂律关系，为了避免引入更多其他的概念，我们不介绍和 𝐶𝑚𝑖𝑛 相关的内容。

上面介绍了三个幂律关系，需要特别强调的是，这些幂律关系中的常数会受到不同数据集、tokenizer方法以及token字典表大小的影响，从而得到不同的拟合结果。

2.2 进一步的结论

从数据集大小的幂律关系和模型参数量的幂律关系出发，通过设计不同的实验，我们可以经验性地得到以下几个进一步的结论：

1. 不同类型的数据会显著影响模型的性能。

在大模型的训练中，通常会使用不同类型的组合数据。数据的多样性和适当的组合对最终模型性能的至关重要。

2.在固定模型总参数量的情况下，不同层数的模型的性能差距比较小。

需要注意的是，这里需要排除掉静态编码的矩阵和位置编码的相关参数。

3.模型的结构会有一定的影响，更好的模型结构会得到更好的尺度定律。

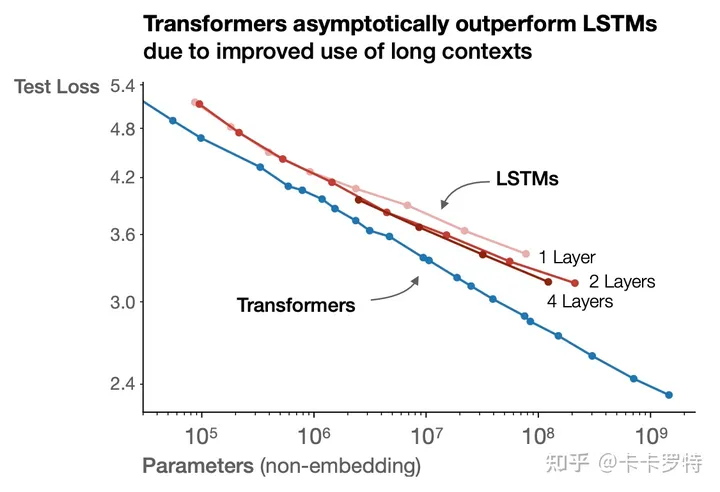
在探索新的模型结构时，判断新模型结构的有效性一个好的方法是检查其是否符合尺度定律，以及尺度定律是否比基准模型更为优越。上图显示Transformer结构优于多层LSTM结构。

2.3 联合幂律关系

除了单个变量和模型性能 𝐿 的幂律关系外，我们还可以建立 𝐷,𝑁 和 𝐿 的联合幂律关系。目前有两类常用的联合幂律关系假设：

在"Scaling Laws for Neural Language Models"中，作者假设联合幂律关系如下：

     (10)

需要注意的是，这里的等常数的值和2.1小节提到的值不一定相同。

在"Training Compute-Optimal Large Language Models"中[3]，作者假设联合幂律关系如下：

     (11)

这里的 𝛼 和 𝛽 为常数， 𝐸 是数据集自身的不可约误差。

通过第一个幂律关系假设，我们可以推导出一个有趣的结论。

当模型的参数量为 𝑁 时，我们需要保证数据集大小 𝐷 大于 才能保证模型不会过拟合。

下面我们详细介绍一下这个值是如何得到的。首先作者利用公式(10)，拟合得到的值：

(12)

接着定义 𝛿𝐿(𝑁,𝐷) :

  (13)

𝐿(𝑁,∞) 表示在无限的数据下，损失的情况。当有无限的数据时，我们认为不会出现过拟合。因此上面公式度量的是在数据集 𝐷 大小的情况下，过拟合的程度。该值越大，表示过拟合越严重，该值等于0，表示没有过拟合。然而，由于一些随机性，即使 𝐷 已经足够的大，不会导致过拟合， 𝐿(𝑁,𝐷) 也不可能恰好等于零。因此，我们可以认为当 𝛿𝐿(𝑁,𝐷) 小于某个上界时， 𝐿(𝑁,𝐷) 就可以近似认为没有过拟合。

这个上界通过估计 𝐿(𝑁,∞) 的方差得到。即选择不同的随机种子，在足够大的数据集上训练，得到不同的性能 𝐿 ，以此估计出方差。在"Scaling Laws for Neural Language Models"中，作者估计的方差为 0.02 。因此，结合公式(10)和(13)：

  (14)

带入前面拟合的估计值，最终可得：

    (15)

需要注意的是，不同的数据集，tokenizer方法，token字典表大小会得到不同的拟合结果，方差估计结果。因此掌握上面的计算流程是很有必要的。

2.4 最优算力分配

𝐶 与 𝐿 的幂律关系告诉我们，为了获取“智能”，我们是需要付出一定的代价的。每增加10倍的计算量，模型的性能就会有一定的提升。在计算量的预算有限的情况下，应该如何分配数据集大小 𝐷 和模型参数量 𝑁 ，使得模型的性能达到最佳呢？

OpenAI和DeepMind给出了两种不同的结论：

OpenAI认为[1]，每增加10倍的计算量，应该让数据集大小增加为约1.8倍，模型参数量增加为约5.5倍。换句话说，OpenAI认为，模型参数量更加的重要。

DeepMind认为[3]，每增加10倍的计算量，应该让数据集大小增加为约3.16倍，模型参数量也增加为约3.16倍。换句话说，DeepMind认为，数据集大小和模型参数量一样重要。

需要注意的是，这里的数据使用的是对应论文中的数据，在实际的应用中它可能会随着使用的数据集，tokenizer方法，token字典表大小而变化。

在上述描述中，最优算力分配实际上忽略了推断时的算力消耗。在实际应用中，我们可能更应优先考虑的是模型的推理速度，而非仅仅追求训练速度最快。这是因为训练时的算力消耗只发生一次，而后续模型推理可能会进行无数次。因此，Meta开源的Llama大语言模型[4]选择了一种不同的策略，他们采用了参数量较小但在推断时消耗计算资源较少的大语言模型。在随后的训练过程中，他们持续扩展训练集，直至模型性能不再提高。

需要注意的是，这并不代表Meta的策略就是最优的。这是因为按照OpenAI和DeepMind的算力分配策略训练出的大语言模型，在尽量不降低模型效果的前提下，可以利用诸如模型蒸馏、模型压缩、模型量化、模型剪枝等技术手段来缩小模型的体积。

2.5 关于模型的性能

通常我们以测试集上的损失来度量模型性能 𝐿 。尽管存在2.1小节提到的三个幂律关系，但为了稍微减小一点损失就付出成倍的模型参数和计算量，这真的是一种划算的策略吗？

实际上，研究者发现，尽管模型的损失只是在稳定下降，但模型在某些下游任务的性能却可能突然出现大幅度的提升，正如下图所示[5]（参考自"Emergent Abilities of Large Language Models"）：

这种由量变所带来的质变，称为涌现。因此，虽然损失只由 𝑙 降低到了 0.9𝑙 ，但这并不等价于“性能”只提升了百分之十。

3. 尺度定律的未来

尺度定律的极限

"Scaling Laws for Neural Language Models"中提到的幂律关系和联合幂律关系其实会推导出一些矛盾，这些矛盾可能能帮助我们思考尺度定律的极限。

在2.3中我们提到，为了防止过拟合，需要数据集大小 𝐷 和模型参数量 𝑁 满足如下的关系：

(16)

在2.4中，我们又提到，按照近似 5.5:1.8 的比例分配关系增加模型参数量 𝑁 和数据集大小 𝐷 ，可以使得损失 𝐿 按照幂律关系不断降低。

然而，很明显，如果不断的按照 5.5:1.8 的比例增加模型参数量 𝑁 和数据集大小 𝐷 ，那么一定存在一个点 𝑁∗,𝐷∗ ，使得。换句话说，按照2.4的结论，在达到 𝑁∗,𝐷∗ 后，继续增加模型参数量和数据集大小，损失 𝐿 会继续降低，但按照2.3的结论，模型会出现过拟合， 𝐿 并不会降低，反而会升高。

为什么会出现这种矛盾呢？"Scaling Laws for Neural Language Models"的作者认为有两种可能：

1. 在 𝑁 和 𝐷 增长到 𝑁∗,𝐷∗ 之前，尺度定律会失效。
2. 𝑁∗,𝐷∗ 点的损失值是自然语言数据自身的不可约误差。

实际上，我们离 𝑁∗,𝐷∗ 还有一定的距离。因为除了自然语言数据外，还有其他模态的数据，例如图像数据，语音数据。这些模态的数据也存在着类似的尺度定律，但在多模态的数据集中，尺度定律的极限更加难以达到。

模型性能的涌现

在2.5小节中，我们提到，随着损失 𝐿 的下降，一些下游任务的性能可能会出现突变，即涌现现象。然而，这种涌现现象无法通过尺度定律进行准确预测。

随着 𝑁 和 𝐷 的进一步增加，损失 𝐿 的进一步降低是否会导致更多的涌现出现仍然是未知的。然而，我们对这种未知充满期待。只要尺度定律尚未达到极限，我们仍有机会显著提升大语言模型的“智能”，即使损失 𝐿 并未大幅下降。

类梅特卡夫定律

尺度定律是通过增加计算量、模型参数和数据集大小来提升单个大语言模型的“智能”水平。

基于大语言模型设计的智能体能够协同合作、任务分工，甚至相互竞争。智能体数量的扩展可能进一步推动智能的涌现，就如同人类文明随着人数的增加以及分工的细化而不断发展一样。

因此，在一个存在多个智能体交互的网络中，可能存在一种类似于梅特卡夫定律[6]的经验法则，即随着网络内可交互智能体数量的增加，整个网络的“智能”也会不断提升。

本书的读者对象是大语言模型的使用者和应用开发者，全书共分为4篇。

• 第1篇讲述机器学习、神经网络的基本概念，自然语言处理的发展历程，以及大语言模型的基本原理。鉴于本书的重点在于大语言模型的应用和二次开发，因此本书将不涉及大语言模型的训练细节。然而，我们仍强烈建议读者熟悉每个关键术语的含义，并了解大语言模型的工作流程，以更好地理解后面的内容。
• 第2篇讲述大语言模型的基础应用技巧。首先，介绍大语言模型常用的3种交互格式。随后，深入讲解提示工程、工作记忆与长短期记忆，以及外部工具等与大语言模型使用相关的概念。最后，对大语言模型生态系统中的关键参与者——ChatGPT的接口与扩展功能进行详解。
• 第3篇讲述大语言模型的进阶应用技巧。首先，介绍如何将大语言模型应用于无梯度优化，从而拓宽大语言模型的应用领域。随后，详细讨论各类基于大语言模型的自主Agent系统，以及微调的基本原理。最后，介绍与大语言模型相关的安全技术。
• 第4篇讲述大语言模型的未来。一方面，探讨大语言模型的生态系统和前景，简要介绍多模态大语言模型和相关的提示工程。另一方面，深入解析大语言模型的尺度定律，并尝试从无损压缩的角度来解析大语言模型具备智能的原因，最后以图灵机与大语言模型的联系作为全书的结尾。

参考

1. ^abKaplan J, McCandlish S, Henighan T, et al. Scaling laws for neural language models[J]. arXiv preprint arXiv:2001.08361, 2020.
2. ^Bahri Y, Dyer E, Kaplan J, et al. Explaining neural scaling laws[J]. arXiv preprint arXiv:2102.06701, 2021.
3. ^abHoffmann J, Borgeaud S, Mensch A, et al. Training compute-optimal large language models[J]. arXiv preprint arXiv:2203.15556, 2022.
4. ^Touvron H, Lavril T, Izacard G, et al. Llama: Open and efficient foundation language models[J]. arXiv preprint arXiv:2302.13971, 2023.
5. ^Wei J, Tay Y, Bommasani R, et al. Emergent abilities of large language models[J]. arXiv preprint arXiv:2206.07682, 2022.
6. ^梅特卡夫定律认为，一个网络的价值与网络中的节点数量的平方成正比。具体而言，如果一个网络有n个节点，那么它的价值大致与n^2成正比。这表明网络的价值随着节点数量的增加呈二次方增长。

这篇关于大语言模型中的第一性原理：Scaling laws的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---