C语言之数据结构之栈和队列的运用

2024-05-05 05:04
文章标签 语言 数据结构 队列 运用 之栈

本文主要是介绍C语言之数据结构之栈和队列的运用，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

    • 1. 用队列实现栈
      • 1.1 思路讲解
      • 1.2 代码实现
    • 2. 用栈实现队列
      • 1.1 思路讲解
      • 1.2 代码实现
    • 总结

在这里插入图片描述
•͈ᴗ•͈ 个人主页：御翮
•͈ᴗ•͈ 个人专栏：C语言数据结构
•͈ᴗ•͈ 欢迎大家关注和订阅!!!

在这里插入图片描述

1. 用队列实现栈

题目描述：

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

  • void push(int x) 将元素 x 压入栈顶。
  • int pop() 移除并返回栈顶元素。
  • int top() 返回栈顶元素。
  • boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

  • 你只能使用队列的标准操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
  • 你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：

输入：
[“MyStack”, “push”, “push”, “top”, “pop”, “empty”]
[ [ ], [1], [2], [ ], [ ], [ ] ]
输出：
[ null, null, null, 2, 2, false ]

解释：

MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

提示：

  • 1 <= x <= 9
  • 最多调用100 次 push、pop、top 和 empty
  • 每次调用 pop 和 top 都保证栈不为空

1.1 思路讲解

首先队列的特性是先入先出，而栈的特性是先入后出

题目说用两个队列实现一个栈

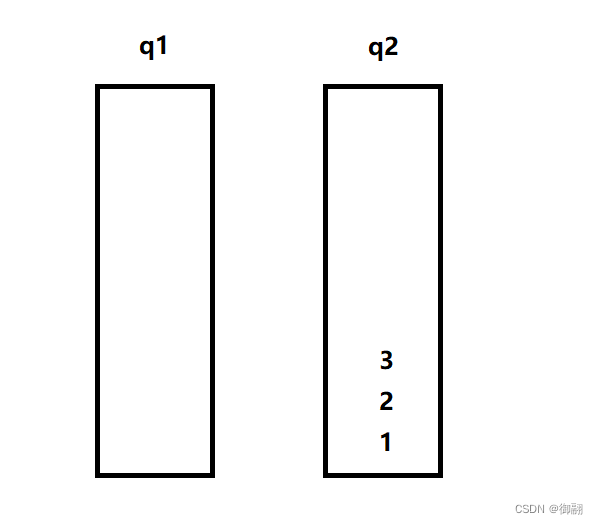
所以当栈为空时我们有两个空队列q1和q2

我们入数据时先默认入q2，假设这里依次入1、2、3

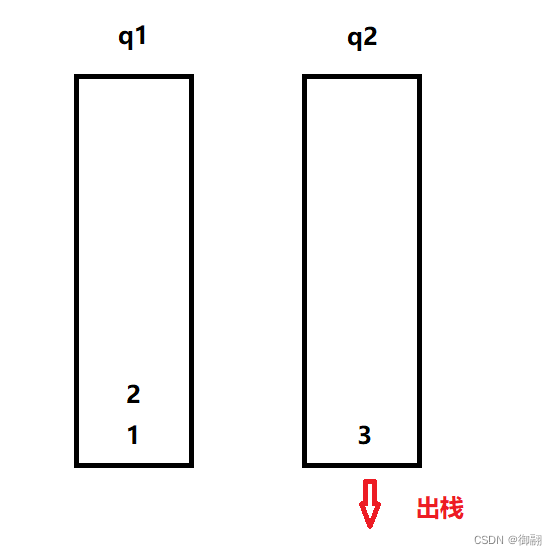
在这里插入图片描述

如果这个时候我们要出栈呢，如果按队列先入先出，我们会拿到1而不是最后入的3

此时我们可以先把1和2依次放入q1中，此时q2中就只剩3，就可以先取出3了

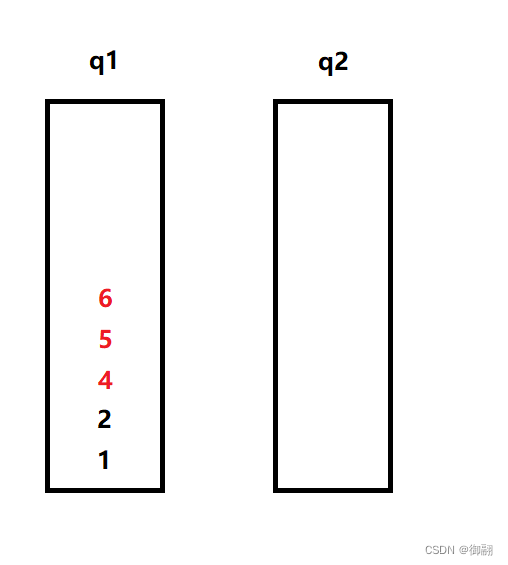
在这里插入图片描述

如果我们接着要放数据，就放入非空的队列q1，这样留一个队列q2为空，就还可以继续这样的出栈操作

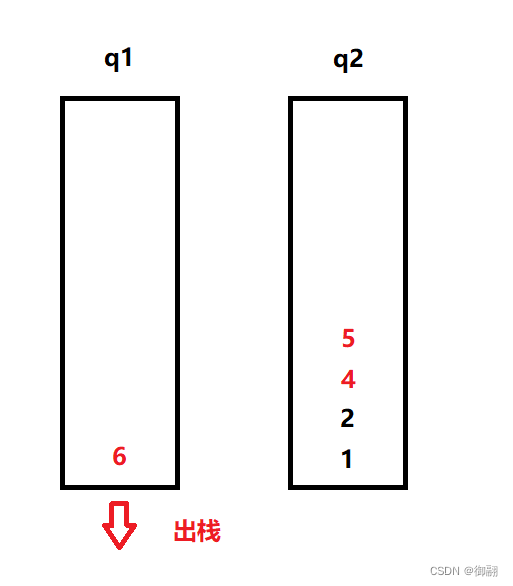
在这里插入图片描述

当我们要继续出栈时，就把前n-1个数据放入空的队列中，再把最后一个数据取出，这样如此颠倒反复，就完成了先入后出的操作

在这里插入图片描述

1.2 代码实现

队列代码：

#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
#include <assert.h>
#include <string.h>typedef int QDatatype;typedef struct QNode
{struct QNode* next;QDatatype data;
}QNode;typedef struct Queue
{QNode* head;QNode* tail;
}Queue;void Init_Queue(Queue* ptr)
{assert(ptr);ptr->head = ptr->tail = NULL;
}
void Destroy_Queue(Queue* ptr)
{assert(ptr);QNode* cur = ptr->head;while (ptr->head != NULL){cur = ptr->head;ptr->head = ptr->head->next;free(cur);}ptr->tail = NULL;
}QNode* Buy_Node()
{QNode* tmp = (QNode*)malloc(sizeof(QNode));return tmp;
}void Print_Queue(Queue* ptr)
{assert(ptr);QNode* cur = ptr->head;while (cur != NULL){printf("%d ", cur->data);cur = cur->next;}printf("\n");
}void Push_Queue(Queue* ptr, QDatatype val)
{assert(ptr);QNode* newnode = Buy_Node();if (newnode == NULL){perror("Push_Queue\n");exit(1);}newnode->data = val;newnode->next = NULL;if (ptr->head == NULL){ptr->head = ptr->tail = newnode;}else{ptr->tail->next = newnode;ptr->tail = newnode;}
}int Queue_Size(Queue* ptr)
{assert(ptr);int count = 0;QNode* cur = ptr->head;while (cur != NULL){cur = cur->next;count++;}return count;
}void Pop_Queue(Queue* ptr)
{assert(ptr);if (ptr->head == NULL){printf("队列中没有元素\n");return;}if (Queue_Size(ptr) == 1){free(ptr->tail);//如果删完了但是没有将tail置为NULL，则case 5 会发生错误，显示队尾元素随机值。ptr->tail = NULL;ptr->head = NULL;return;}QNode* pop = ptr->head;ptr->head = ptr->head->next;free(pop);
}QDatatype Queue_Front(Queue* ptr)
{assert(ptr);return ptr->head->data;
}QDatatype Queue_Back(Queue* ptr)
{assert(ptr);return ptr->tail->data;
}int Check_Empty(Queue* ptr)
{assert(ptr);if (Queue_Size(ptr))return 0;elsereturn 1;
}//以上是自己创建的队列，因为c语言没有队列

队列实现栈代码：

typedef struct 
{Queue q1;Queue q2;
} MyStack;// 创建栈
MyStack* myStackCreate() 
{MyStack* tmp = (MyStack*)malloc(sizeof(MyStack));if (tmp == NULL) // 开辟空间可能失败，失败则终止程序{printf("Fail: myStackCreate\n");exit(1);}Init_Queue(&tmp->q1); // 我们的栈由两个队列组成，所以初始化要调用队列的初始化Init_Queue(&tmp->q2);return tmp;
}// 数据入栈
void myStackPush(MyStack* obj, int x) 
{if (Check_Empty(&obj->q1)) // 哪个队列有元素就往哪放，两个都没有就默认放q2，保证只有一个队列有数据{Push_Queue(&obj->q2, x);}elsePush_Queue(&obj->q1, x);
}// 数据出栈
int myStackPop(MyStack* obj) 
{//题目保证每次调用pop时栈都不为空，不用考虑为空时的popif (Check_Empty(&obj->q1)) // 哪个队列有数据就将n-1个数据放到另一个队列，剩下的最后一个元素就是栈顶元素，直接出栈{int sum = Queue_Size(&obj->q2); // 获取队列元素个数nfor (int i = 0; i < sum - 1; i++) // 将前n-1个数据放到另一个空队列{Push_Queue(&obj->q1, Queue_Front(&obj->q2));Pop_Queue(&obj->q2);}QDatatype tmp = Queue_Front(&obj->q2); // 保存最后一个元素的值，再pop，因为要返回出栈元素的值Pop_Queue(&obj->q2);return tmp;}else{int sum = Queue_Size(&obj->q1);for (int j = 0; j < sum - 1; j++){Push_Queue(&obj->q2, Queue_Front(&obj->q1));Pop_Queue(&obj->q1);}QDatatype tmp = Queue_Front(&obj->q1);Pop_Queue(&obj->q1);return tmp;}
}// 获取栈顶元素
int myStackTop(MyStack* obj) 
{//题目保证每次调用top时栈都不为空，不用考虑为空时的topif (Check_Empty(&obj->q1)) // 因为我们前面入栈时保证了只有一个队列有数据，所以队尾元素就是栈顶元素{return Queue_Back(&obj->q2);}elsereturn Queue_Back(&obj->q1);
}// 判断栈是否为空
bool myStackEmpty(MyStack* obj) 
{if (Check_Empty(&obj->q1) && Check_Empty(&obj->q2)) // 栈由两个队列组成，两个队列都为空栈就为空{return true;}elsereturn false;
}// 销毁栈
void myStackFree(MyStack* obj) 
{Destroy_Queue(&obj->q1); // 消耗栈要销毁里面的两个队列Destroy_Queue(&obj->q2);free(obj);
}

2. 用栈实现队列

题目描述：

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）。

实现 MyQueue 类：

  • void push(int x) 将元素 x 推到队列的末尾
  • int pop() 从队列的开头移除并返回元素
  • int peek() 返回队列开头的元素
  • boolean empty() 如果队列为空，返回 true ；否则，返回 false

注意：

  • 你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
  • 你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

示例 ：

输入：
[“MyQueue”, “push”, “push”, “peek”, “pop”, “empty”]
[ [ ], [1], [2], [ ], [ ], [ ] ]
输出：
[ null, null, null, 1, 1, false ]

解释：

MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

提示：

1 <= x <= 9
最多调用 100 次 push、pop、peek 和 empty
假设所有操作都是有效的 （例如，一个空的队列不会调用 pop 或者 peek 操作）

1.1 思路讲解

首先栈的特性是先入后出，而队列的特性是先入先出

题目说用两个栈实现一个队列

所以当队列为空时我们有两个空栈

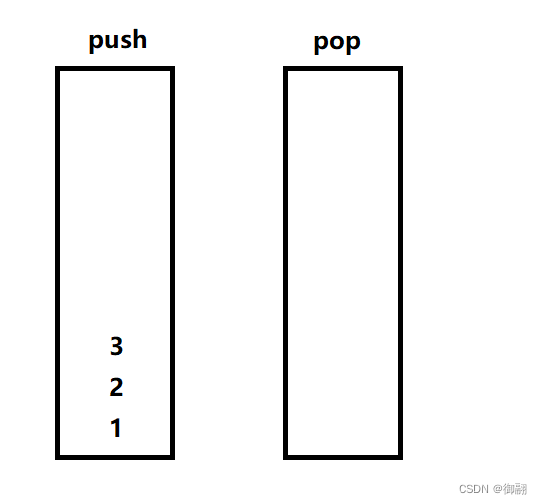
我们给这两个栈分别命名为push和pop

我们入数据只往push里放

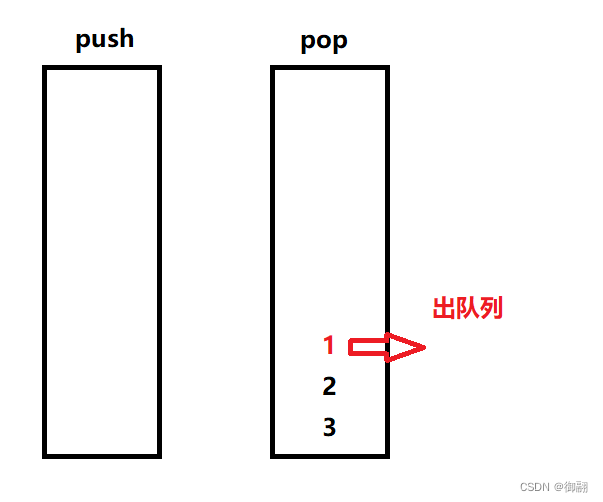
在这里插入图片描述

出数据的话，如果pop为空，我们就把push栈里面的数据全放进pop栈里，再出栈，就取到了队头的元素

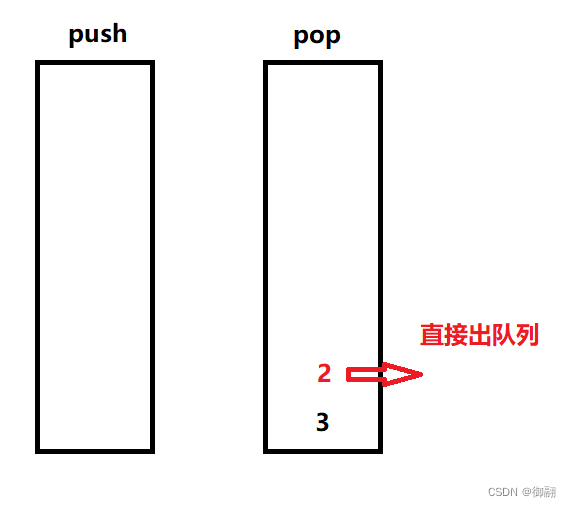
在这里插入图片描述

如果pop不为空，就直接出栈就好了

在这里插入图片描述

后序有数据也是直接放在push，push只进行入栈，pop只进行出栈，不像用队列实现栈一样要来回颠倒。

1.2 代码实现

栈代码：

#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
#include <assert.h>
#include <errno.h>typedef int STDataType;typedef struct Stack
{STDataType* stack;int size;int capacity;
}Stack;void Init_Stack(Stack* ptr)
{assert(ptr);STDataType* tmp = (STDataType*)malloc(3 * sizeof(STDataType));if (tmp == NULL){perror("Init_Stack\n");exit(1);}ptr->stack = tmp;ptr->capacity = 3;ptr->size = 0;
}void Destroy_Stack(Stack* ptr)
{assert(ptr);free(ptr->stack);ptr->stack = NULL;
}void Check_Capacity(Stack* ptr)
{assert(ptr);if (ptr->size == ptr->capacity){STDataType* tmp = (STDataType*)realloc(ptr->stack, 2 * ptr->capacity * sizeof(STDataType));if (tmp == NULL){perror("Check_Capacity\n");exit(1);}ptr->stack = tmp;ptr->capacity *= 2;}
}void Print_Stack(Stack* ptr)
{assert(ptr);for (int i = 0; i < ptr->size; i++){printf("%d ", ptr->stack[i]);}printf("\n");
}void Push_Stack(Stack* ptr, STDataType val)
{assert(ptr);Check_Capacity(ptr);ptr->stack[ptr->size] = val;ptr->size++;
}void Pop_Stack(Stack* ptr)
{assert(ptr);ptr->size--;
}STDataType Top_Stack(Stack* ptr)
{assert(ptr);return ptr->stack[ptr->size - 1];
}int Size_Stack(Stack* ptr)
{assert(ptr);return ptr->size;
}int Empty_Stack(Stack* ptr)
{assert(ptr);if (ptr->size == 0)return 1;elsereturn 0;
}typedef struct 
{Stack push;Stack pop;
} MyQueue;

栈实现队列代码：

// 创建队列
MyQueue* myQueueCreate() 
{MyQueue* queue = (MyQueue*)malloc(sizeof(MyQueue));if (queue == NULL) // 开辟空间有可能失败，失败则终止程序{perror("myQueueCreate");exit(1);}Init_Stack(&queue->push); // 初始化队列要初始化里面的栈Init_Stack(&queue->pop);return queue;
}// 数据入队列
void myQueuePush(MyQueue* obj, int x) 
{Push_Stack(&obj->push, x); // 数据只入push栈
}// 数据出队列
int myQueuePop(MyQueue* obj) 
{if (Empty_Stack(&obj->pop)) // 如果pop栈为空，就要从push栈里面把数据拿过来{int sum = Size_Stack(&obj->push); // 获取push中的元素个数nfor (int i = 0; i < sum; i++){Push_Stack(&obj->pop, Top_Stack(&obj->push));Pop_Stack(&obj->push);}}int ret = Top_Stack(&obj->pop); // 先储存队头元素再出队列，因为题目要返回队头元素Pop_Stack(&obj->pop);return ret;
}// 获取队头元素
int myQueuePeek(MyQueue* obj) 
{if (Empty_Stack(&obj->pop)) // 如果pop栈为空，那就把push栈里面的元素拿过来{int sum = Size_Stack(&obj->push);for (int i = 0; i < sum; i++){Push_Stack(&obj->pop, Top_Stack(&obj->push));Pop_Stack(&obj->push);}}return Top_Stack(&obj->pop); // 队头元素就是pop栈中的栈顶元素，因为pop栈内的元素是push栈内的元素顺序颠倒过来
}// 判断队列是否为空
bool myQueueEmpty(MyQueue* obj) 
{if (Empty_Stack(&obj->push) && Empty_Stack(&obj->pop)) // 两个栈都为空，队列就为空{return true;}elsereturn false;
}// 销毁队列
void myQueueFree(MyQueue* obj) 
{Destroy_Stack(&obj->push);  // 销毁队列要销毁里面的两个栈Destroy_Stack(&obj->pop);free(obj);					// 不要忘记释放这个空间
}

总结

两个队列实现栈需要来回颠倒。
两个栈实现队列要确定一个push和一个pop。

这篇关于C语言之数据结构之栈和队列的运用的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/960856。

相关文章

C语言中位操作的实际应用举例

C语言中位操作的实际应用举例

《C语言中位操作的实际应用举例》：本文主要介绍C语言中位操作的实际应用,总结了位操作的使用场景,并指出了需要注意的问题,如可读性、平台依赖性和溢出风险,文中通过代码介绍的非常详细,需要的朋友可以参... 目录1. 嵌入式系统与硬件寄存器操作2. 网络协议解析3. 图像处理与颜色编码4. 高效处理布尔标志集合
阅读更多...
Go语言开发实现查询IP信息的MCP服务器

Go语言开发实现查询IP信息的MCP服务器

《Go语言开发实现查询IP信息的MCP服务器》随着MCP的快速普及和广泛应用,MCP服务器也层出不穷,本文将详细介绍如何在Go语言中使用go-mcp库来开发一个查询IP信息的MCP... 目录前言mcp-ip-geo 服务器目录结构说明查询 IP 信息功能实现工具实现工具管理查询单个 IP 信息工具的实现服
阅读更多...
C 语言中enum枚举的定义和使用小结

C 语言中enum枚举的定义和使用小结

《C语言中enum枚举的定义和使用小结》在C语言里,enum（枚举）是一种用户自定义的数据类型,它能够让你创建一组具名的整数常量,下面我会从定义、使用、特性等方面详细介绍enum,感兴趣的朋友一起看... 目录1、引言2、基本定义3、定义枚举变量4、自定义枚举常量的值5、枚举与switch语句结合使用6、枚
阅读更多...
Java的栈与队列实现代码解析

Java的栈与队列实现代码解析

《Java的栈与队列实现代码解析》栈是常见的线性数据结构,栈的特点是以先进后出的形式,后进先出,先进后出,分为栈底和栈顶,栈应用于内存的分配,表达式求值,存储临时的数据和方法的调用等,本文给大家介绍J... 目录栈的概念（Stack）栈的实现代码队列（Queue）模拟实现队列(双链表实现)循环队列（循环数组
阅读更多...
Redis消息队列实现异步秒杀功能

Redis消息队列实现异步秒杀功能

《Redis消息队列实现异步秒杀功能》在高并发场景下,为了提高秒杀业务的性能,可将部分工作交给Redis处理,并通过异步方式执行,Redis提供了多种数据结构来实现消息队列,总结三种,本文详细介绍Re... 目录1 Redis消息队列1.1 List 结构1.2 Pub/Sub 模式1.3 Stream 结
阅读更多...
SpringKafka错误处理(重试机制与死信队列)

SpringKafka错误处理(重试机制与死信队列)

《SpringKafka错误处理(重试机制与死信队列)》SpringKafka提供了全面的错误处理机制,通过灵活的重试策略和死信队列处理,下面就来介绍一下,具有一定的参考价值,感兴趣的可以了解一下... 目录引言一、Spring Kafka错误处理基础二、配置重试机制三、死信队列实现四、特定异常的处理策略五
阅读更多...
Go 语言中的select语句详解及工作原理

Go 语言中的select语句详解及工作原理

《Go语言中的select语句详解及工作原理》在Go语言中,select语句是用于处理多个通道（channel）操作的一种控制结构,它类似于switch语句,本文给大家介绍Go语言中的select语... 目录Go 语言中的 select 是做什么的基本功能语法工作原理示例示例 1：监听多个通道示例 2：带
阅读更多...
C语言函数递归实际应用举例详解

C语言函数递归实际应用举例详解

《C语言函数递归实际应用举例详解》程序调用自身的编程技巧称为递归,递归做为一种算法在程序设计语言中广泛应用,：本文主要介绍C语言函数递归实际应用举例的相关资料,文中通过代码介绍的非常详细,需要的朋... 目录前言一、递归的概念与思想二、递归的限制条件 三、递归的实际应用举例（一）求 n 的阶乘（二）顺序打印
阅读更多...
C#数据结构之字符串(string)详解

C#数据结构之字符串(string)详解

《C#数据结构之字符串(string)详解》：本文主要介绍C#数据结构之字符串(string),具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录转义字符序列字符串的创建字符串的声明null字符串与空字符串重复单字符字符串的构造字符串的属性和常用方法属性常用方法总结摘
阅读更多...
C语言中的数据类型强制转换

C语言中的数据类型强制转换

《C语言中的数据类型强制转换》：本文主要介绍C语言中的数据类型强制转换方式,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录C语言数据类型强制转换自动转换强制转换类型总结C语言数据类型强制转换强制类型转换：是通过类型转换运算来实现的，主要的数据类型转换分为自动转换
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2