【经典论文阅读1】FM模型——搜推算法里的瑞士军刀

本文主要是介绍【经典论文阅读1】FM模型——搜推算法里的瑞士军刀，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

• 全文由『说文科技』原创出品，文章同步更新于公众号『说文科技』。版权所有，翻版必究。
  

FM模型发表于2010年，它灵活好用且易部署。作者行文极其流畅，作者首先对要处理的问题进行介绍，接着作者提出FM模型，这个模型与SVM的关键区别在于FM模型在稀疏数据上具备更好的性能。FM模型的底层思想就是用特征向量（可以看出本文已经初步具备embedding的思想）的点积代替简单的权重从而得到更好的权重表示，这种思想巧妙地绕开了稀疏数据的影响。现在FM模型仍然在搜推行业上发挥作用，对于业务刚起步的公司来说，它不仅效果好，而且性能强，故大多数人称之为搜索算法里的瑞士军刀。

0. 前言

看这篇文章前，首先需要理解one-hot向量和SVM。

0.1 理解one-hot向量。

其实在embedding被广泛接受之前，业界一直使用的都是one-hot向量。这个one-hot向量很好理解，举个例子来说：如果一个词表大小为7（假设词典就是：『别和捞女谈恋爱』），那么别这个字的表示就是[1,0,0,0,0,0,0]。但是使用one-hot的一个最大的缺点就是：向量太稀疏了，只有一个1，其它全是0。而业界之前的做法就是将类似词表这种特征信息作为模型的输入，所以模型就需要对稀疏值有一个很好的处理能力（，但实际上大多数模型做不到）。

0.2 熟悉SVM。

简单来说：SVM算法就是需要去构建一个超平面，这个超平面可以很好的将数据进行分类，达到的分类效果是：使得支持向量到超平面最短的距离达到最大。 如果对这段话不能理解，可以参考我之前的算法工程师面试题十之支持向量机（SVM） 进行学习。SVM在稀疏特征上的效果很差，所以才出现了本文的FM模型。

1. 摘要

FM模型，是一个将factorization model(因式分解)模型和SVM模型优点结合在一起的模型。它具备如下优点：

• FMs are a general predictor working with any real valued feature vector.
  这意思就是说：FMs是一个通用的预测器，这个预测器的输入可以是任何真实的特征向量

• 对于巨大稀疏值这一问题，FM模型依然可以做出交互。【这一点就是FM的关键思想】
  

• FMs subsume many of the most successful approaches for the task of collaborative filtering including biased MF, SVD++ [2], PITF [3] and FPMC.
  意思就是说：FMs 归纳了协同过滤任务中大多数的成功的方法：例如 biased MF，SVD++，PITF，FPMC等。

总结一下，就是如下这些优点：

2. 思想

下面这句话就是本文最核心的思想：

the FM models the interaction by factorizing it. 就是说通过因式分解的方式建模交互， 交互的过程就是通过点积实现。

3. 模型

3.1. FM 模型

下面这段表述就清楚地说明了FM模型长什么样子：

$x_i$ 、 $x_j$ 是特征向量 $x$ 的第$i$ 维和 第$j$ 维上的值。

通过式子（1），可以看出，FM模型与逻辑回归的不同之处就在于多计算了
$$\sum _{i=1}^n\sum _{j=i+1}^n<v_i,v_j>x_i{x}_j$$
这一部分。假设$V_{3\ast 2}$，那么这部分就等价于：$<v_1,v_2>x_1{x}_2+<v_1,v_3>x_1{x}_3+<v_2,v_3>x_2{x}_3$。这么做的效果就相当于让各个特征进行充分的交互，每个交互的权值由 $<x_i,x_j>$决定。

3.2. FM模型的表达能力

3.3. 稀疏数据下的参数估计

这段话看着挺头疼的，看懂了也就明白作者说的是哪会儿事儿了。这个思想很简单就是『因式分解』，再说的详细点儿，就是用embedding间点积的思想代替以前单个值作为特征交互的权重。

• 如果直接使用权重 $w_{A,ST}=0$ 表示Alice和 Star Wars间的交互，则显得过于绝对了（Alice没看过这部电影或者没评价这部电影，不代表她没情绪啊）；

那么有没有好的衡量方法呢？显然是有的？如果一步做不成的事儿，那就分两步做。将第$i$个特征都抽象成一个向量$v_i$(所有的特征向量的表示就成了一个矩阵$V$)，那么用向量间的点积去表示权重，这样总会避免得到0值吧！

上图完美的诠释了什么叫一图胜千言。说实话，在现在这个鱼龙混杂的论文年代，看到这种非常细致，非常认真的作图的论文真的很少（至少这个作者的论文比我本人写论文画的图要好太多）。

3.4. 复杂度

经过一系列的转换计算，可以得出FM模型的复杂度是 O(kn)。详细的转换计算过程如下：

3.5. 损失优化

使用随机梯度下降（SGD） 的方法来更新参数值。

3.6. d-way FM模型

上面介绍FM模型时，都是将交互矩阵的维度取成2，也就是所说的2-way FM模型，那么泛化成 d-way FM模型，就是下面这样：

4. 效果

4.1 FM vs SVM in sparse data

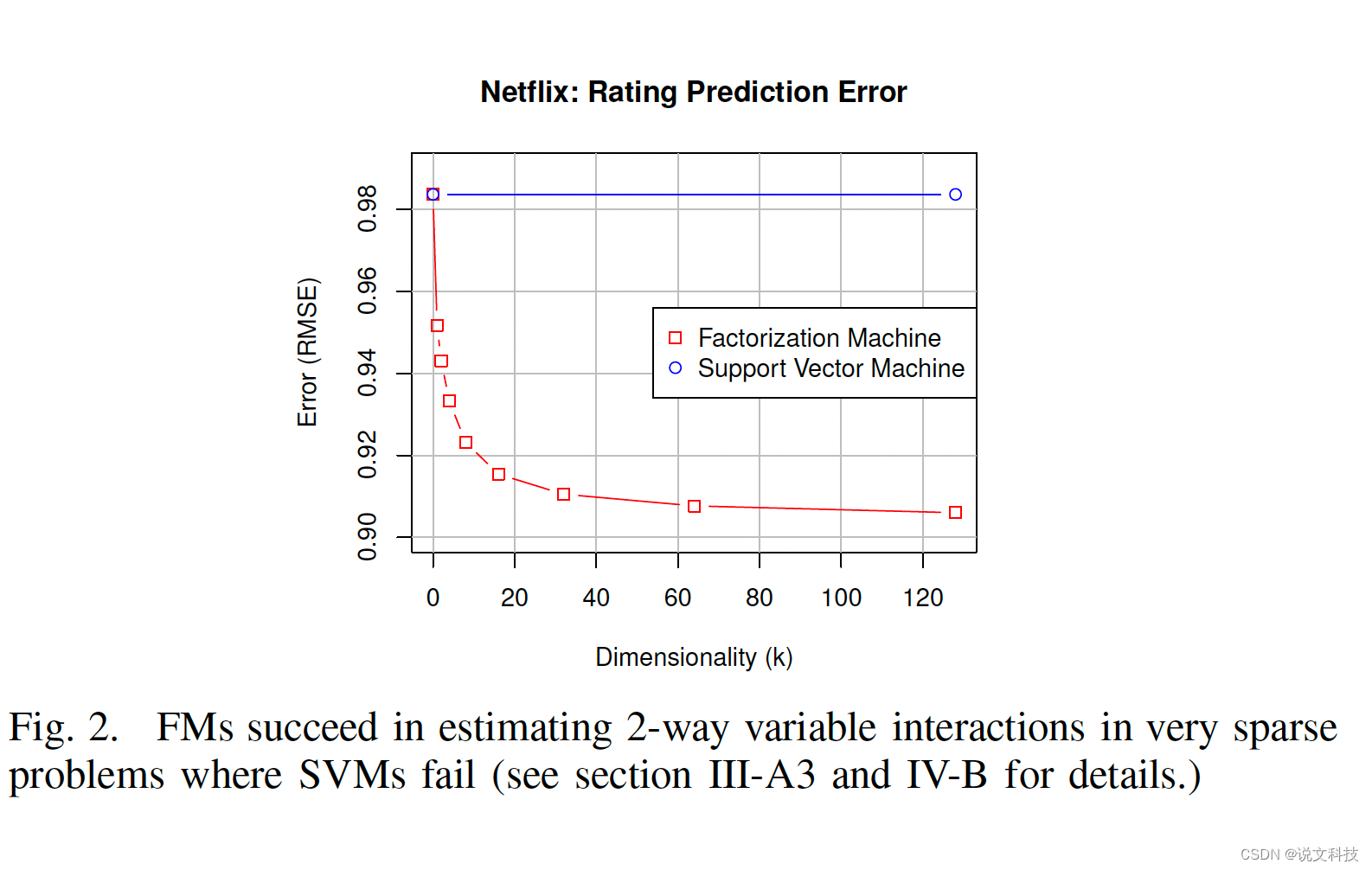
5. 疑问

5.1. 什么是pairwise training data？

也就是一个tuple = (x,y)，这个tuple (x,y) 表示 x 应该 比y 的排名更靠前，可以结合下面这篇文章理解：

5.2. 稀疏的含义是什么？

指的就是一个向量 x 的大多数元素都是zero。下面给出了一个简单的示例：

One reason for huge sparsity is that the underlying problem deals with large categorical variable domains.
原因就是：每项特征的类别都太多了，搞成one-hot 形式就会有很多稀疏值。

5.3 为啥拿特征之间的交互？

通过文章中的表达式：

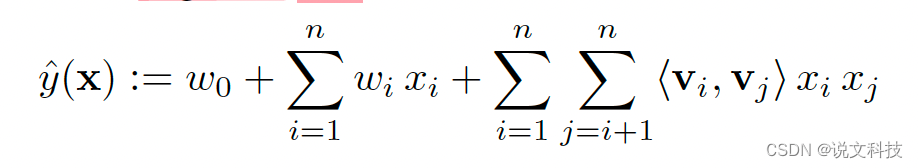
5.4 SVM 未能在collaborative filtering 领域发挥价值的原因是：

hyperplane 也就是分类的超平面；non-linear kernel 也就是让你学习过程中十分头疼的那些核方法。

5.5 复杂度里的k，n 分别表达什么？

上文中提到$k$是交互矩阵的纬度，$n$代表输入特征向量$x$的维度

5.6 下文中的 degree d = 2是啥意思？

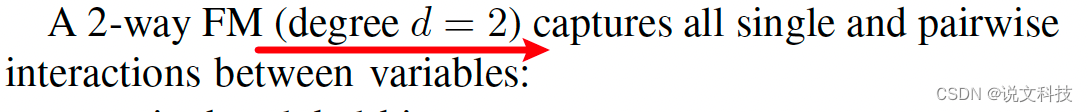
很简单，就是指交互向量的维度。

5.7 为啥用点积模拟交互？

那不然用啥捏？

6. 好句分享

In the remainder of this paper, we will show the relationships between factorization machines and support vector machines as well as matrix, tensor and specialized factorization models.

in the remainder of this paper, 在文章的剩余部分…

这篇关于【经典论文阅读1】FM模型——搜推算法里的瑞士军刀的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---