在2-3-4树上实现连接与分裂操作的算法与实现

本文主要是介绍在2-3-4树上实现连接与分裂操作的算法与实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

引言

2-3-4树是一种平衡搜索树，它保证了树的高度被有效控制，从而为查找、插入和删除操作提供了较好的时间复杂度。在本篇文章中，我们将探讨如何在2-3-4树上实现连接与分裂操作，这些操作对于动态集合的合并和划分非常有用。

1. 维护2-3-4树结点的高度属性

为了维护2-3-4树中每个结点的高度，我们可以将高度作为结点的一个属性。在进行插入、查找和删除操作时，需要适当更新相关结点的高度。

伪代码示例

class Node {int key[7]; // 最多4个关键字int count;  // 当前结点的关键字数量int height; // 当前结点的高度Node children[5]; // 最多4个孩子
}// 更新结点的高度
function updateHeight(node) {node.height = 1 + max(height(node.children[1]), height(node.children[2]), ..., height(node.children[4]))
}// 插入操作后更新高度
function insert(root, key) {// ... 插入操作逻辑updateHeight(parent)// 可能需要进行树的再平衡
}// 删除操作后更新高度
function delete(root, key) {// ... 删除操作逻辑updateHeight(parent)// 可能需要进行树的再平衡
}

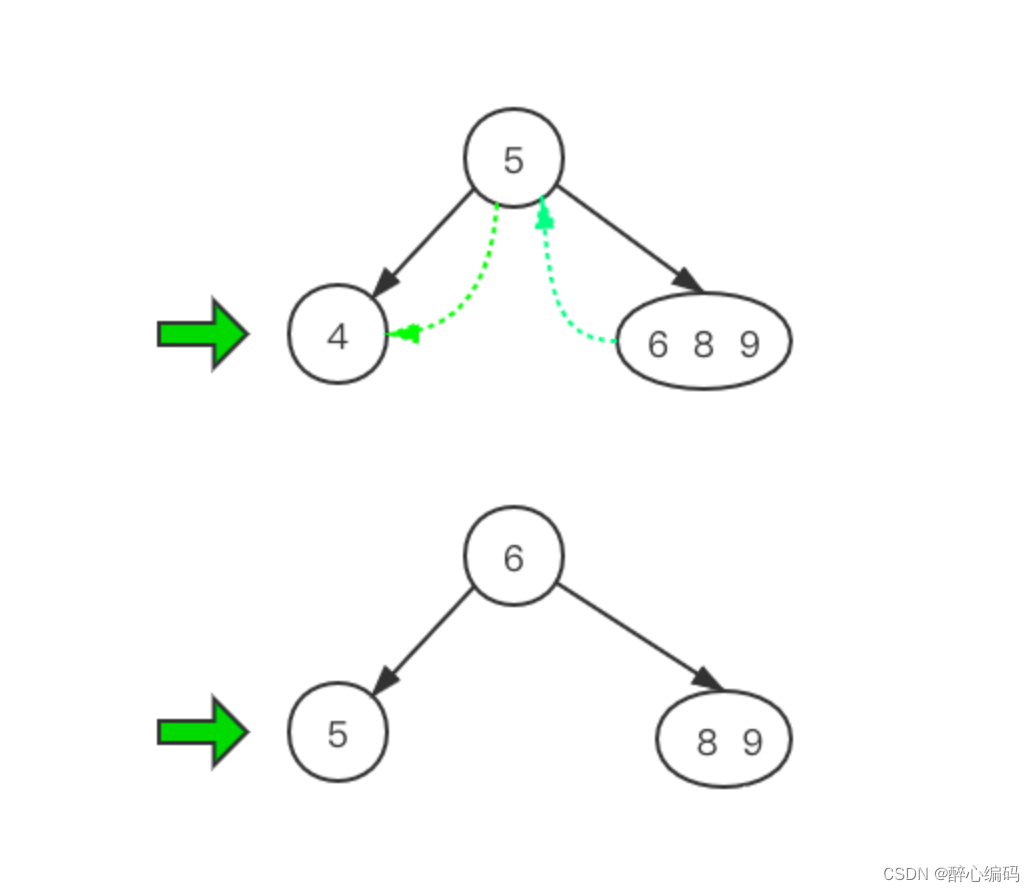
2. 实现连接操作

连接操作的目的是将两个2-3-4树和一个中间关键字合并为一个。操作的时间复杂度为O(1 + |h’ - h"|)，其中h’和h"分别是两棵树的高度。

伪代码示例

function combineTrees(T', T", key) {if height(T') > height(T") thenreturn combineTrees(T", T', key) // 保持T'为较矮的树end ifT'.root.key[T'.root.count] = key // 将中间关键字加入T'T'.root.count = T'.root.count + 1T'.root.children[T'.root.count + 1] = T".root // T"成为T'的一个孩子T".root = null // 移除T"的根return T'
}

3. 证明简单路径p的划分性质

对于一棵2-3-4树T，给定一个关键字k，路径p从根到k将小于k的关键字集合S’和大于k的关键字集合S"进行了划分。集合S’中的任意树Ti和集合S"中的任意关键字k’都满足y < k’ < x，其中y是Ti中的任意关键字。

4. 实现分裂操作

分裂操作是连接操作的逆过程，它将一个2-3-4树分成两个子树。利用连接操作，我们可以将S’和S"中的关键字分别拼成新的2-3-4树T’和T"。

伪代码示例

function splitTree(T, key) {S' = {} // 集合存储小于key的元素S" = {} // 集合存储大于key的元素node = T.rootwhile node.count > 0 and key > node.key[1] do // 寻找key的位置if shouldGoLeft(node, key) thenS'.add(node)node = node.children[1]elseS".add(node)node = node.children[2]end ifend whileif node.count > 0 thenS'.add(node) // key所在的结点加入S'elseS".add(node) // key应该被插入的位置在node之后end ifT' = buildTreeFromSet(S') // 从S'构建树T'T" = buildTreeFromSet(S") // 从S"构建树T"return T', T"
}// 从集合构建2-3-4树
function buildTreeFromSet(set) {// ... 构建树的逻辑
}

C代码示例

由于C语言中没有内置的树结构，实现2-3-4树的C代码会相当复杂，并且超出了简短回答的范围。通常，你需要定义一个结构体来表示树的结点，并实现一系列函数来维护树的平衡和进行连接与分裂操作。

结论

在2-3-4树上实现连接与分裂操作需要对树的结构和性质有深刻的理解。通过精心设计算法，我们可以确保这些操作的时间复杂度满足预期，从而保持2-3-4树作为一种高效的数据结构。

这篇关于在2-3-4树上实现连接与分裂操作的算法与实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---