本文主要是介绍【深度学习】第一门课 神经网络和深度学习 Week 4 深层神经网络,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
🚀Write In Front🚀
📝个人主页:令夏二十三
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏:深度学习
💬总结:希望你看完之后,能对你有所帮助,不足请指正!共同学习交流 🖊
文章目录
4.1 深层神经网络概述
4.2 前向传播和反向传播
4.2.1 前向传播
4.2.2 反向传播
4.5 使用深层表示的原因
4.7 参数和超参数
4.1 深层神经网络概述
深层神经网络,其实就是在浅层神经网络这篇文章中提到的示例的基础上增加隐藏层数量罢了,没有本质的区别:

4.2 前向传播和反向传播
4.2.1 前向传播
前向传播很简单,就是从左到右的计算罢了,使用向量化计算的话,就是先喂入神经网络第一层的输入值,也就是 A[0] ,一整个训练样本的输入特征,这就是这条链的第一个前向函数的输入,重复这个步骤就可以计算出这个神经网络的前向传播结果了。
4.2.2 反向传播
从右到左,逐步计算导数,这就是反向传播,步骤如下:
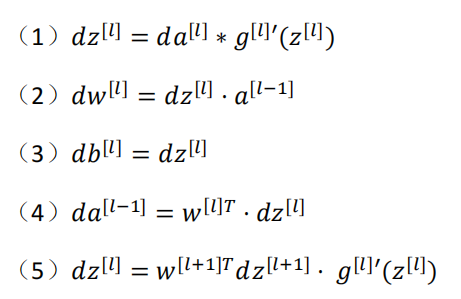
下面用智谱总结一下前向传播和反向传播的目的:
神经网络中的前向传播(Forward Propagation)和反向传播(Back Propagation)是训练神经网络的两个关键过程。
前向传播的目的是为了计算神经网络的输出。在监督学习的情况下,给定的输入数据通过神经网络各层的加权运算和非线性激活函数的作用,最终得到预测结果。这一过程是逐层进行的,每层神经元的输出成为下一层的输入,直到最后一层输出结果。前向传播可以理解为神经网络对输入数据的响应过程,它展示了网络在当前权重和偏置参数配置下如何处理信息。
反向传播的目的是为了调整神经网络的参数(即权重和偏置),使得神经网络的预测结果更接近于真实标签。在计算出前向传播的预测结果后,通过比较预测结果和真实结果之间的差异(即损失函数),反向传播算法计算这些差异如何影响网络的每一层参数。基于这些计算,使用梯度下降等优化算法来调整网络参数,目的是减少损失函数的值,提高模型的性能。反向传播是神经网络能够从错误中学习并逐步改进的关键机制。
总结来说,前向传播是神经网络进行预测的过程,而反向传播则是神经网络学习的过程。两者共同作用,使得神经网络能够通过训练数据不断优化自身参数,提高预测的准确性。
4.5 使用深层表示的原因
深度神经网络之所以通常需要一定深度的层次结构,主要是因为深度结构能够提供以下几个优势:
特征层次化:深度神经网络能够通过多个隐藏层逐步将输入数据从原始特征转换成更高层次、更抽象的特征表示。每一层都可以学习到不同层次的特征,例如,第一层可能只识别边缘和纹理,而更高层则能识别复杂的对象结构。这种层次化的特征学习是深度学习相比于浅层学习的一个重要优势。
非线性建模能力:由于每个隐藏层都使用了非线性激活函数,深度神经网络能够建模非常复杂的函数。深度网络可以通过组合多个非线性变换来捕捉输入和输出之间复杂的关系。
参数共享和泛化:在深度网络中,尤其是在卷积神经网络中,参数是通过在输入数据的多个位置共享来减少模型参数数量的。这种参数共享不仅减少了过拟合的风险,还提高了模型对未见数据的泛化能力。
层次化的表征:深度网络能够学习到数据的层次化表征,这种表征可以捕捉到数据中的内在结构和分布。这种层次化表征有助于网络在不同的抽象层次上理解和处理信息。
复杂的决策边界:在分类问题中,深度网络能够学习到非常复杂的决策边界,这对于处理高度重叠的分类问题非常有用。
然而,并不是所有问题都需要非常深的网络。有些问题可能比较简单,使用浅层网络就足够了。深度网络的训练通常需要更多的数据和计算资源,并且可能更难以调试。因此,选择网络的深度需要根据具体问题的复杂性和可用的资源来决定。在实际应用中,通常会通过实验来确定最佳的网络结构。
4.7 参数和超参数
在深度神经网络中,参数和超参数是两个不同的概念:
参数(Parameters): 参数是神经网络模型内部的变量,它们是模型通过训练数据学习到的。参数决定了神经网络如何将输入映射到输出。在监督学习中,这些参数是通过优化过程(如梯度下降)调整的,以便模型能够更好地拟合训练数据。主要的参数包括:
- 权重(Weights):连接神经网络的每个神经元之间的数值,它们决定了信息在网络中的传递强度。
- 偏置(Biases):加到每个神经元输出上的常数,它们允许模型输出不为零,即使输入全部为零。
在训练过程中,目标是最小化损失函数,这通常是通过更新权重和偏置来实现的。
超参数(Hyperparameters): 超参数是模型外部的配置参数,它们不是通过训练数据学习到的,而是由研究人员或工程师设置的。超参数决定了模型的架构、学习过程和训练方式。超参数的选择对模型的性能有重要影响,通常需要通过实验和经验来确定。主要的超参数包括:
- 学习率(Learning Rate):在参数更新过程中,决定参数更新步长的数值。
- 批量大小(Batch Size):在每次参数更新中使用的数据样本数量。
- 迭代次数(Number of Epochs):在整个数据集上运行梯度下降的次数。
- 网络层数(Number of Layers):神经网络中隐藏层的数量。
- 每层的神经元数量(Number of Neurons per Layer):每个隐藏层中神经元的数量。
- 激活函数(Activation Functions):用于引入非线性到网络中的函数,如ReLU、Sigmoid或Tanh。
- 正则化参数(Regularization Parameters):如L1/L2正则化中的惩罚系数,用于防止过拟合。
超参数通常需要通过交叉验证等方式进行调整和优化,以便找到最优的模型配置。与参数不同,超参数的调整不直接涉及损失函数的最小化过程。
这篇关于【深度学习】第一门课 神经网络和深度学习 Week 4 深层神经网络的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







