本文主要是介绍R语言学习—6—多元相关与回归分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1、引子
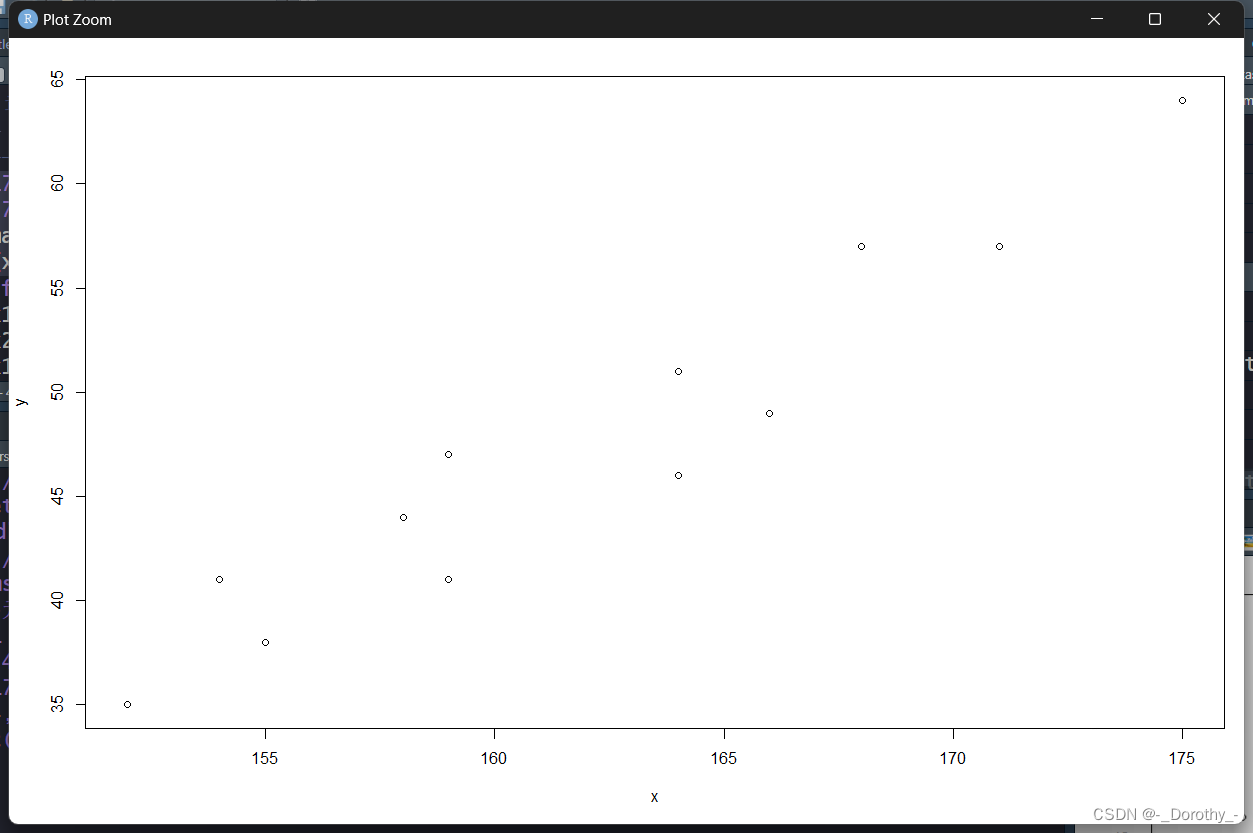
x=c(171,175,159,155,152,158,154,164,168,166,159,164) #身高
y=c(57,64,41,38,35,44,41,51,57,49,47,46) #体重
par(mar=c(5,4,2,1)) #设定图距离画布边缘的距离:下5,左4,上2,右1
plot(x,y)

2、相关系数假设检验


3、简单回归分析



4、案例
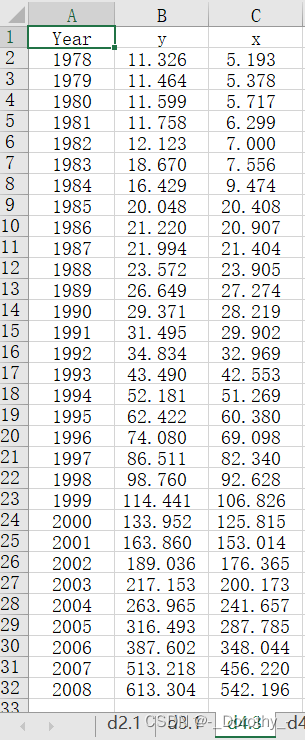
代码
install.packages("openxlsx")
library(openxlsx)d4.3=read.xlsx('adstats.xlsx','d4.3',rowNames=T);d4.3 #读取adstats.xlsx表格d4.3数据
fm=lm(y~x,data=d4.3) #一元线性回归模型
fm #显示回归结果
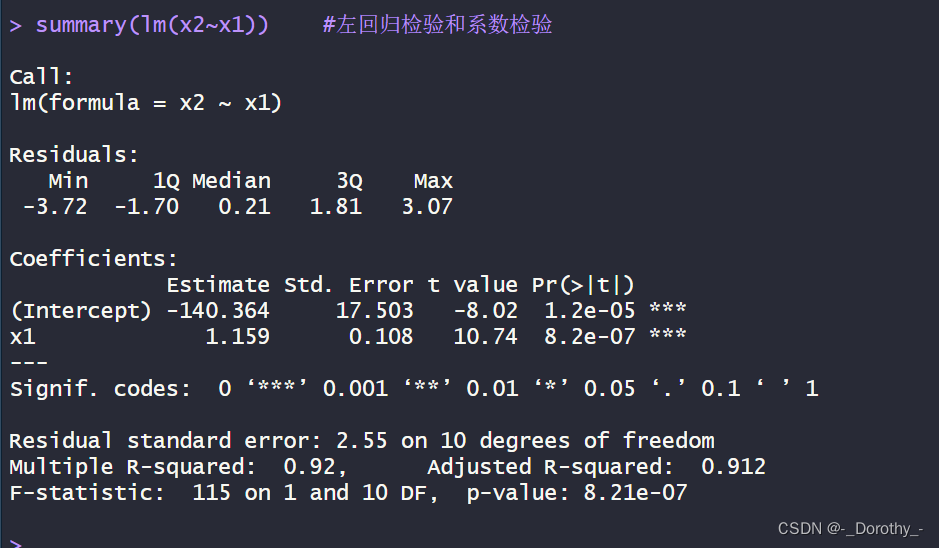
summary(lm(x2~x1)) #左回归检验和系数检验
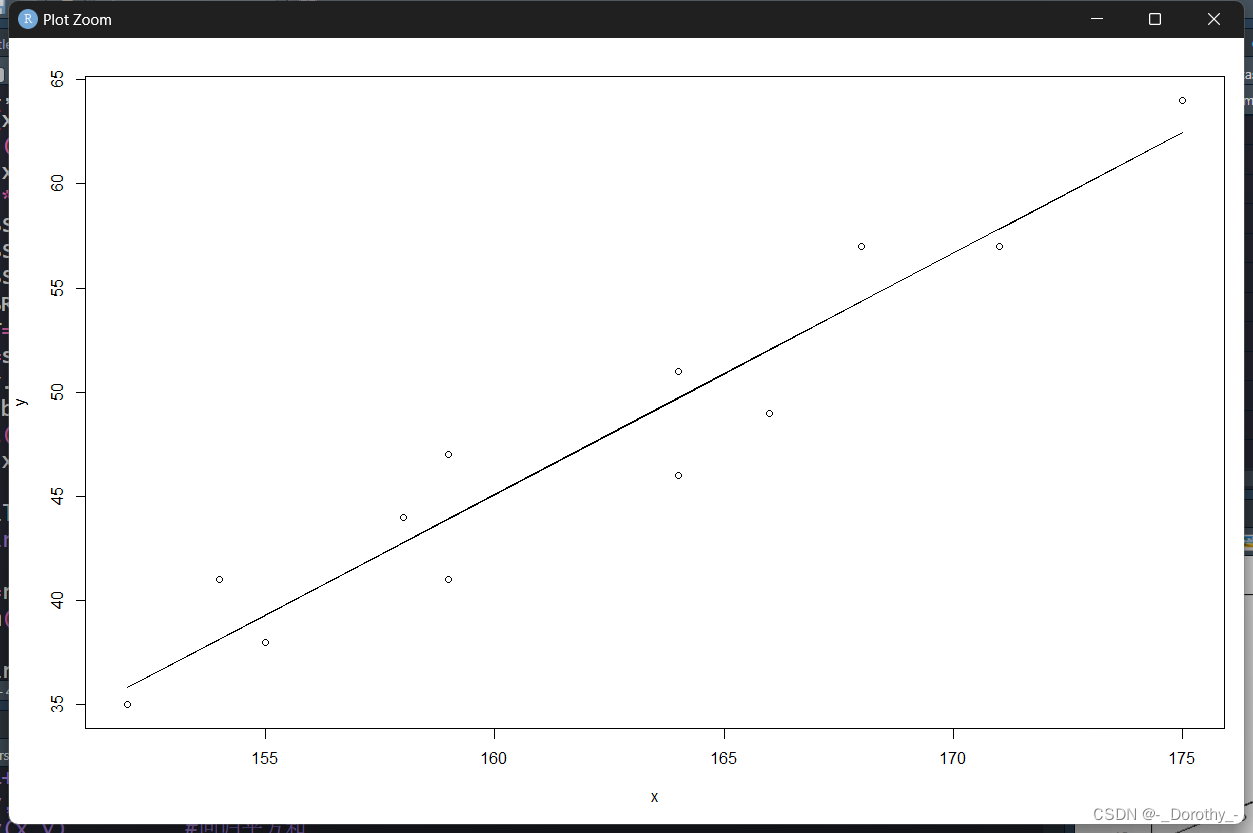
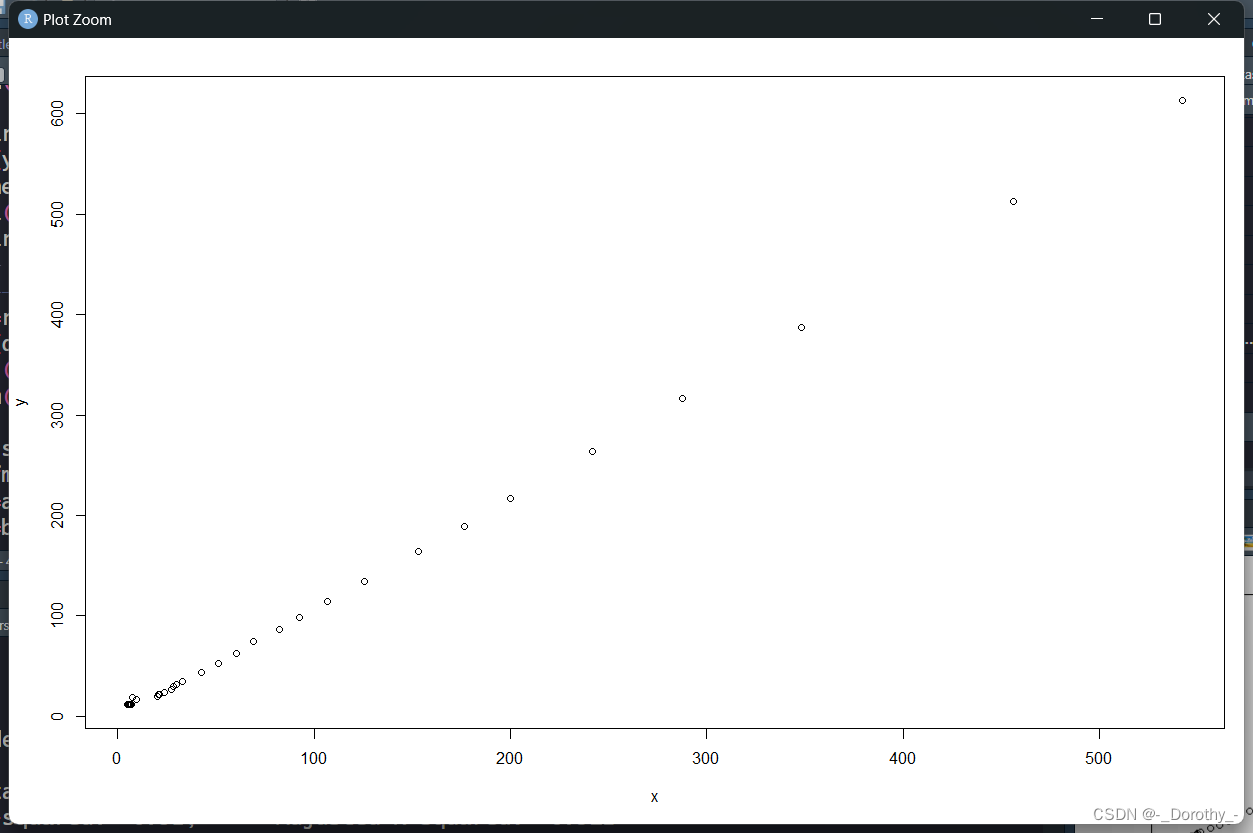
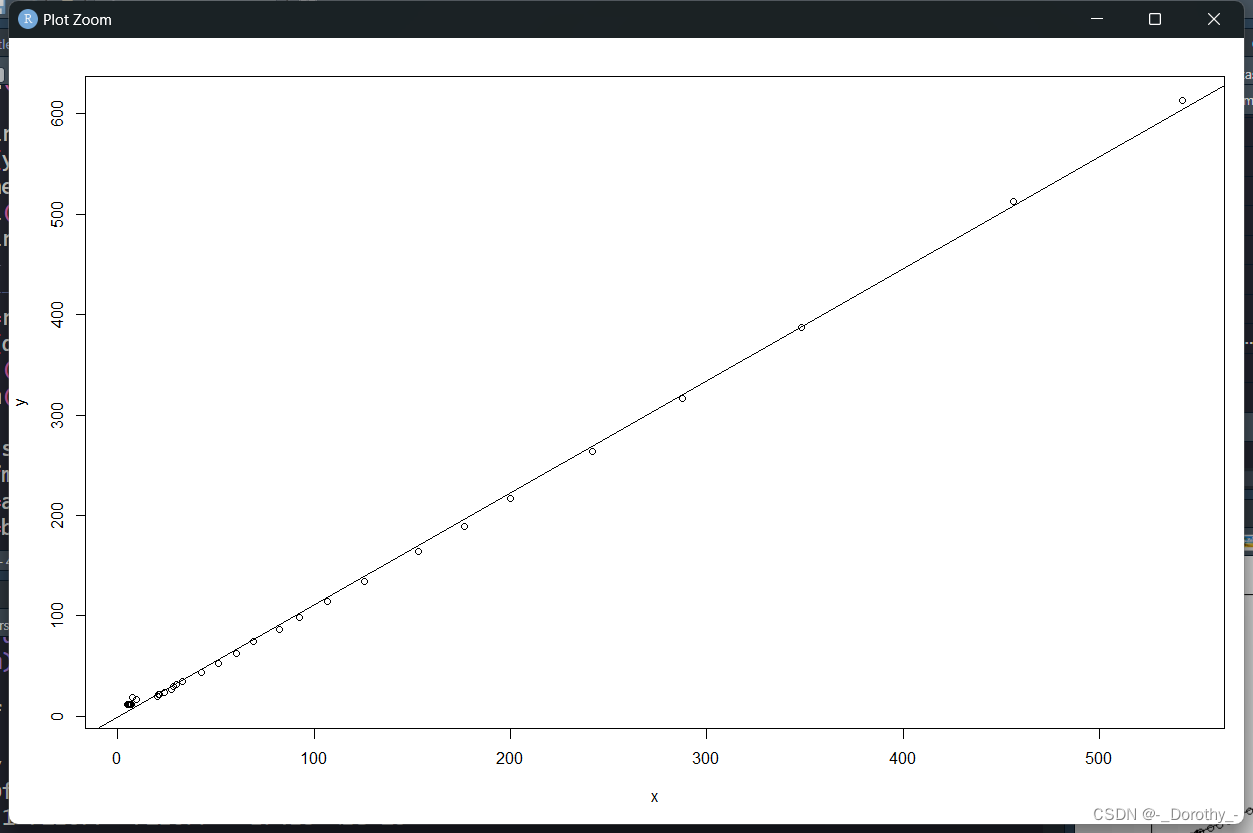
plot(y~x,data=d4.3) #做散点图
abline(fm) #添加回归线
anova(fm) #模型方差分析
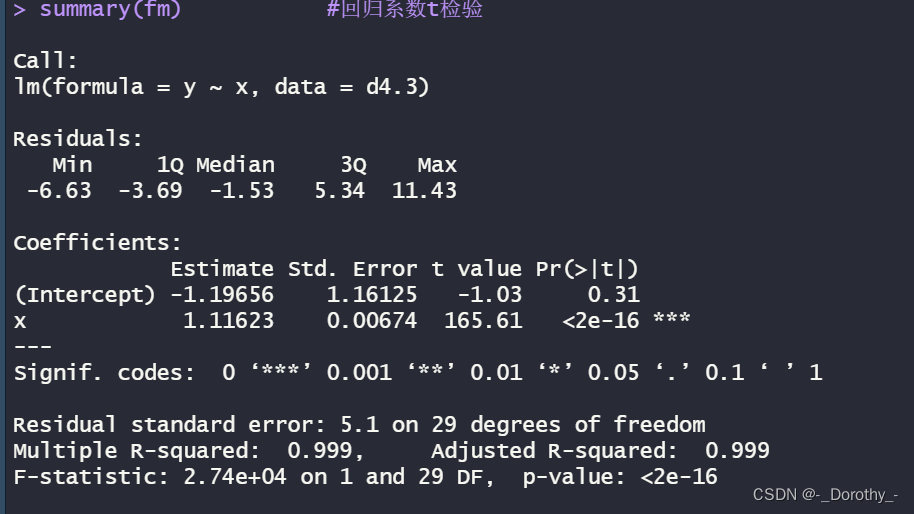
summary(fm) #回归系数t检验






5、多元线性回归分析
(1)d4.4数据
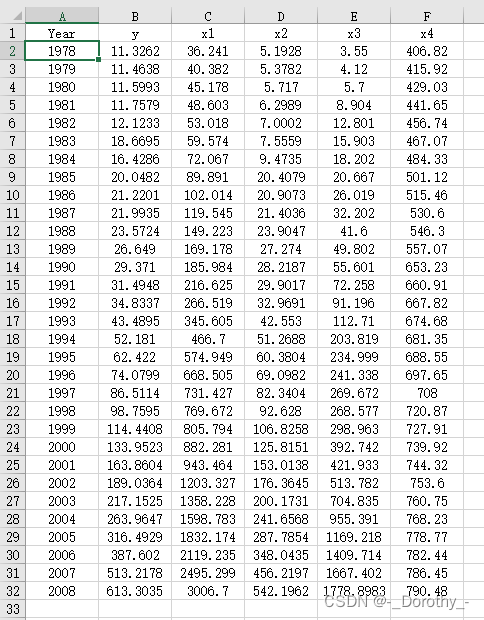
(2)代码
d4.4=read.xlsx('adstats.xlsx','d4.4',rowNames=T);d4.4 #读取adstats.xlsx表格d4.4数据
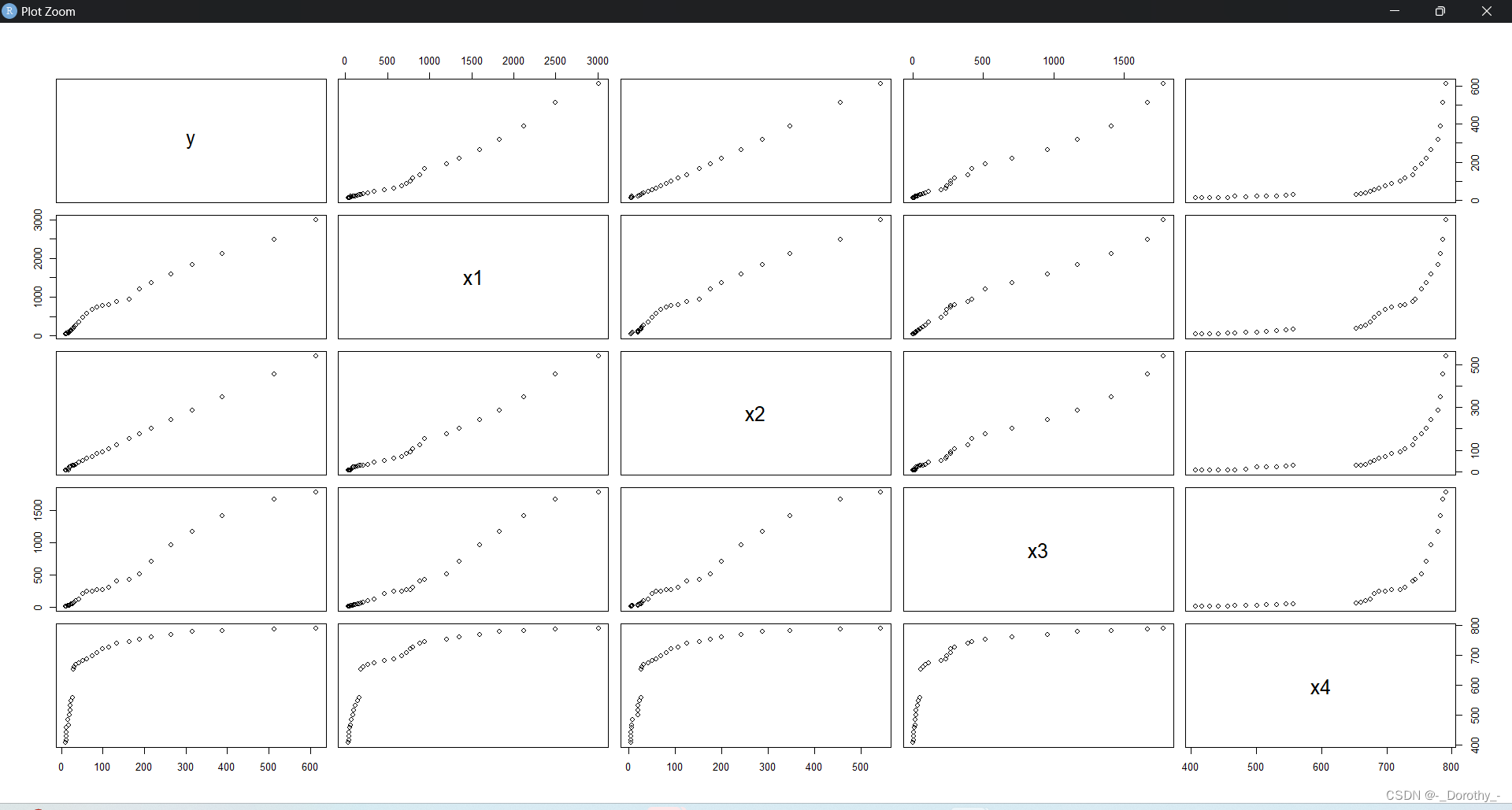
plot(d4.4,gap=0) #两两变量的散点图,参数gap为每个小图形之间的距离
pairs(d4.4,gap=0) #绘制散点图
fm=lm(y~x1+x2+x3+x4,data=d4.4);fm #建立多元回归模型coef.sd<-function(fm){ #标准回归系数b=fm$coef;bsi=apply(fm$model,2,sd);sibs=b[-1]*si[-1]/si[1]bs
}
coef.sd(fm) #标准回归系数
(3)矩阵图
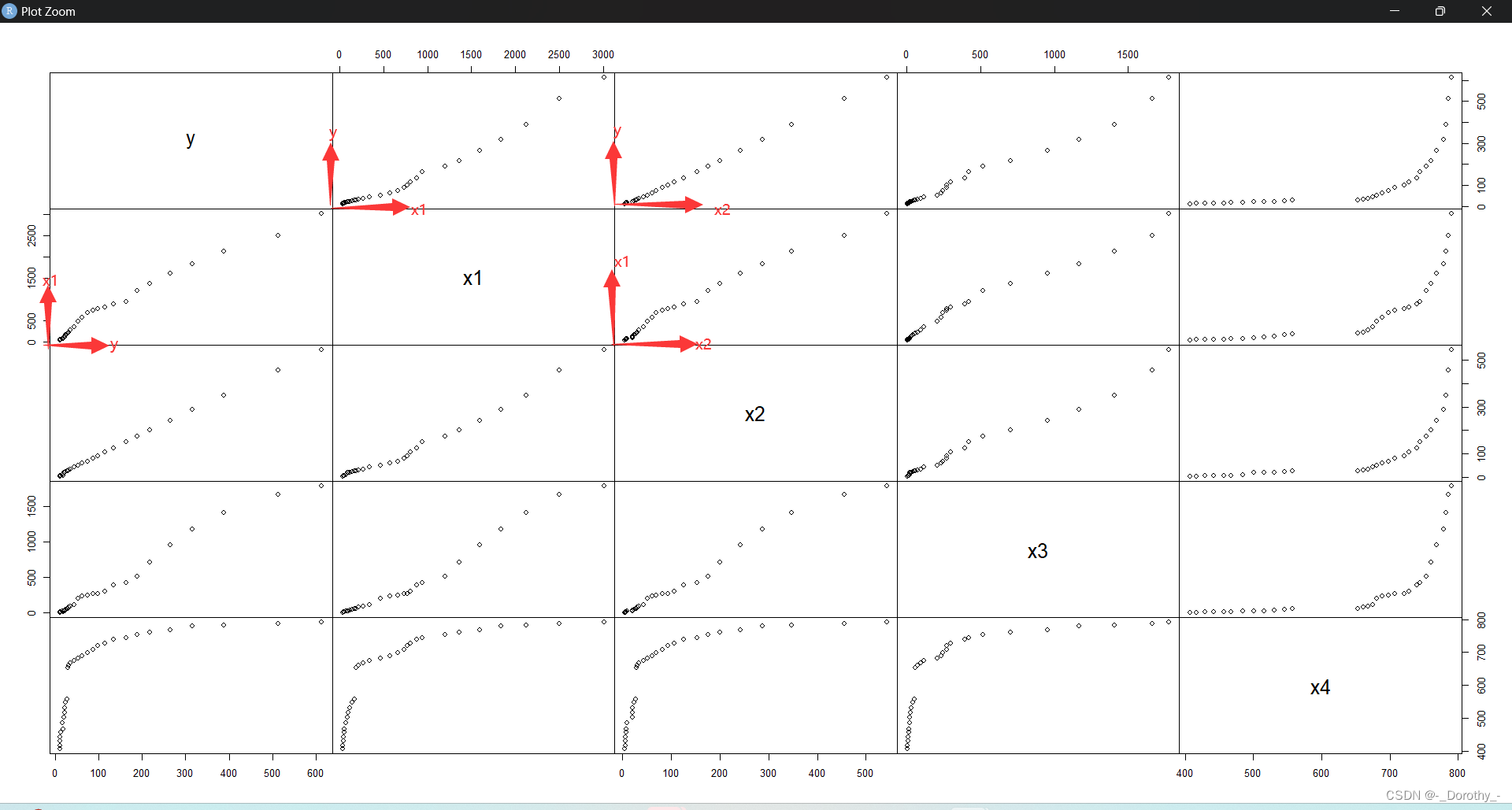
(4)回归模型
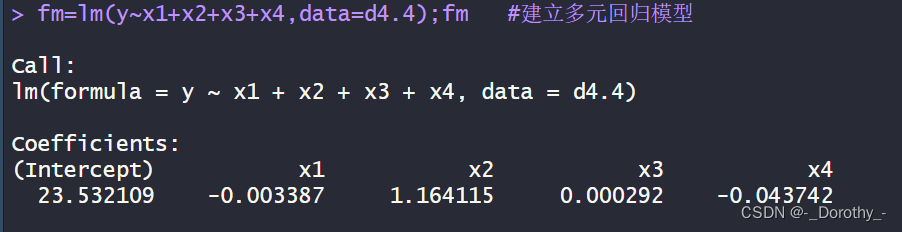
(5)计算标准回归系数
1、coef.sd <- function(fm):这行代码定义了一个名为 coef.sd 的函数,它接受一个参数 fm,表示一个回归模型。
2、b = fm c o e f ; b :这行代码从回归模型 f m 中提取出系数,并将其赋值给变量 b 。然后将这些系数返回。 3 、 s i = a p p l y ( f m coef; b:这行代码从回归模型 fm 中提取出系数,并将其赋值给变量 b。然后将这些系数返回。 3、si = apply(fm coef;b:这行代码从回归模型fm中提取出系数,并将其赋值给变量b。然后将这些系数返回。3、si=apply(fmmodel, 2, sd); si:这行代码计算了每个自变量(模型中的解释变量)的标准差。fm$model 提取了回归模型 fm 的模型数据(包括自变量和因变量),apply 函数在每列上应用 sd 函数来计算标准差,并将结果存储在变量 si 中。
4、bs = b[-1] * si[-1] / si[1]:这行代码计算了标准化的回归系数。首先,b[-1] 提取了除截距以外的所有系数,si[-1] 提取了除因变量以外的所有标准差,然后通过除以第一个标准差 si[1] 来标准化这些系数。结果存储在变量 bs 中。
5、bs:最后,函数返回标准化的回归系数 bs。

6、多元线性回归模型检验
(1)方差分析
anova(fm)
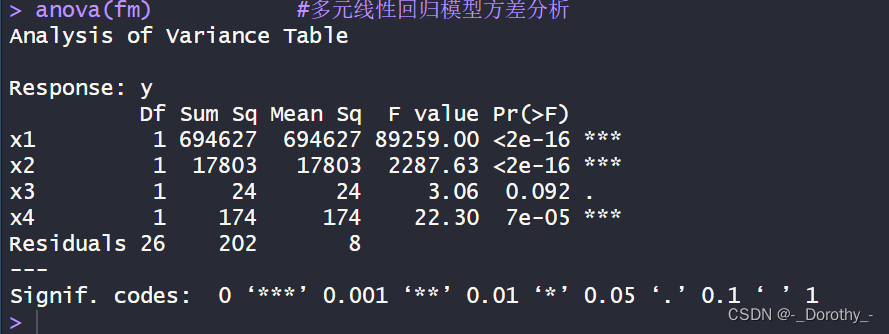
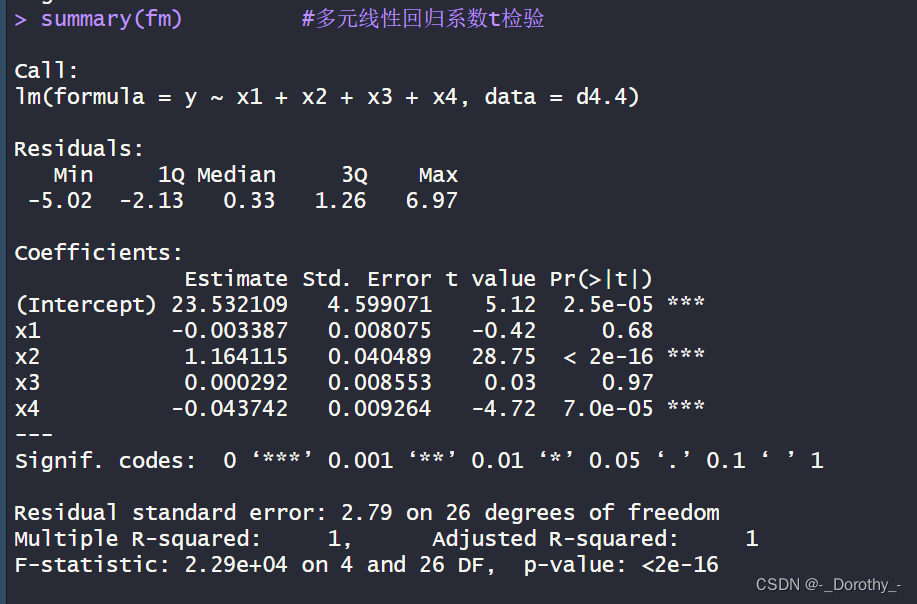
(2)多元线性回归t检验
summary(fm)
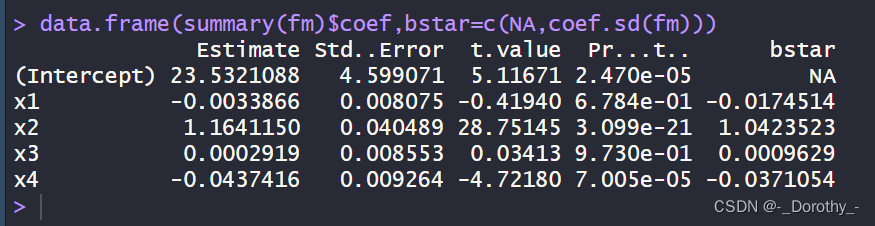
data.frame(summary(fm)$coef,bstar=c(NA,coef.sd(fm)))
首先,data.frame(summary(fm) c o e f ) 这部分代码是在创建一个数据框,其中包含了对象 f m (回归模型)的系数摘要。 s u m m a r y ( f m ) coef) 这部分代码是在创建一个数据框,其中包含了对象fm(回归模型)的系数摘要。summary(fm) coef)这部分代码是在创建一个数据框,其中包含了对象fm(回归模型)的系数摘要。summary(fm)coef会返回一个包含模型系数及其统计信息的列表,然后data.frame()函数将这些信息转化为一个数据框的形式。
其次,bstar=c(NA,coef.sd(fm)) 这部分代码是在设置一个名为’bstar’的参数,其值为c(NA,coef.sd(fm))。这里,NA表示该位置是缺失的或未定义的,而coef.sd(fm)是在获取模型系数的标准差。
总结来说,这段代码的目的是创建一个包含模型系数摘要和标准差的数据框,并将’bstar’参数设置为模型系数的标准差和缺失值的组合。
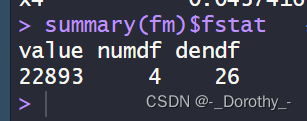
(3)提取F统计量的相关信息
summary(fm)$fstat

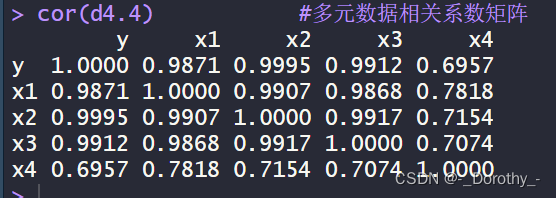
7、多元相关分析
cor(d4.4) #多元数据相关系数矩阵
yX = d4.4
pairs(yX) #多元数据散点图
msa.cor.test(d4.4) #多元数据相关系数检验
msa.cor.test(d4.4) #多元数据相关系数检验

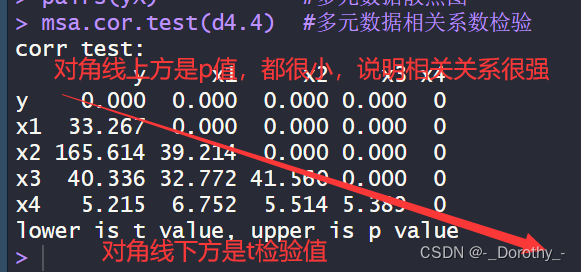
8、复相关分析
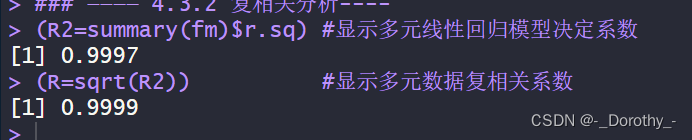
(2)多元线性回归模型的决定系数(决定系数R^2)
多元线性回归模型的决定系数(决定系数R^2)用于衡量模型对观察变量方差的解释程度。决定系数是一个介于0和1之间的数值,其值越接近1,表示模型对数据的解释能力越强。
具体而言,决定系数表示模型中自变量与因变量的总体方差之间的比例。例如,如果因变量的总方差是100,而模型解释了其中75的方差,那么决定系数就是75%。
在多元线性回归模型中,决定系数R2是对模型整体解释能力的总体评估。它可以帮助我们了解模型中自变量对因变量的贡献程度,以及模型预测的准确性。决定系数R2的值越大,说明模型对数据的拟合程度越好。
(1)复相关系数r
多元数据复相关系数是一种统计量,用于衡量多个变量之间的复相关程度。在多元回归分析中,它表示因变量与多个自变量之间的复相关关系。
具体来说,多元数据复相关系数描述了因变量与所有自变量之间的总效应,即所有自变量的总效应对因变量的影响程度。如果多元数据复相关系数较高,说明因变量与多个自变量之间的复相关关系较强,即因变量受多个自变量的共同影响较大。
在实际应用中,多元数据复相关系数可以用于评估多个变量之间的相关性,帮助我们理解这些变量之间的相互作用关系,并为我们提供更全面、深入的信息,以便做出更明智的决策。
9、回归变量的选择方法
(1)变量选择标准

cp统计量和bic统计量


1、x1, x2, x3, x4:这些是模型中的自变量。每个星号 * 表示该自变量被模型选中了。
2、adjR2:这是调整后的 R-squared 值,用于衡量模型对数据的拟合程度。数值越接近1,表示模型对数据的拟合程度越好。
3、Cp:这是 Mallows’ Cp 统计量,用于评估模型的预测准确度和模型的复杂度。通常情况下,Cp 越接近于自变量的数量,表示模型越好。
4、BIC:这是贝叶斯信息准则(Bayesian Information Criterion),也是一种模型选择准则,用于在考虑模型拟合优度和模型复杂度的情况下选择模型。BIC 值越小越好。
- 根据给出的结果
1、调整后的 R-squared 值都非常接近于1,这表示模型对数据的拟合程度很好。
2、Mallows’ Cp 统计量和 BIC 值也都很小,这说明模型的预测准确度较高且模型的复杂度较低。
因此,根据给出的结果,可以得出结论:这个模型的拟合程度很好,且没有明显的过拟合现象。
(2)逐步回归分析
(1)向前引入,向后剔除
这段输出展示了逐步回归法(stepwise regression)中向前引入法和向后剔除法的变量选择结果。
-
向前引入法(forward selection):从一个空模型开始,逐步引入自变量,直到不再有改进(AIC值最小)为止。在这个例子中,初始模型包含了所有的自变量(x1、x2、x3、x4),然后根据AIC逐步引入,直到不再有改进为止。最终,最佳模型包含了自变量 x1、x2、x4。
-
向后剔除法(backward elimination):从包含所有自变量的模型开始,逐步剔除自变量,直到不再有改进(AIC值最小)为止。在这个例子中,初始模型也包含了所有的自变量,然后根据AIC逐步剔除,直到不再有改进为止。最终,最佳模型同样包含了自变量 x1、x2、x4。
这些结果反映了模型的拟合程度和模型的复杂度之间的平衡。最终的模型选择了 x1、x2、x4 这三个自变量,因为它们能够在保持模型简洁的同时最大程度地解释因变量的变异。
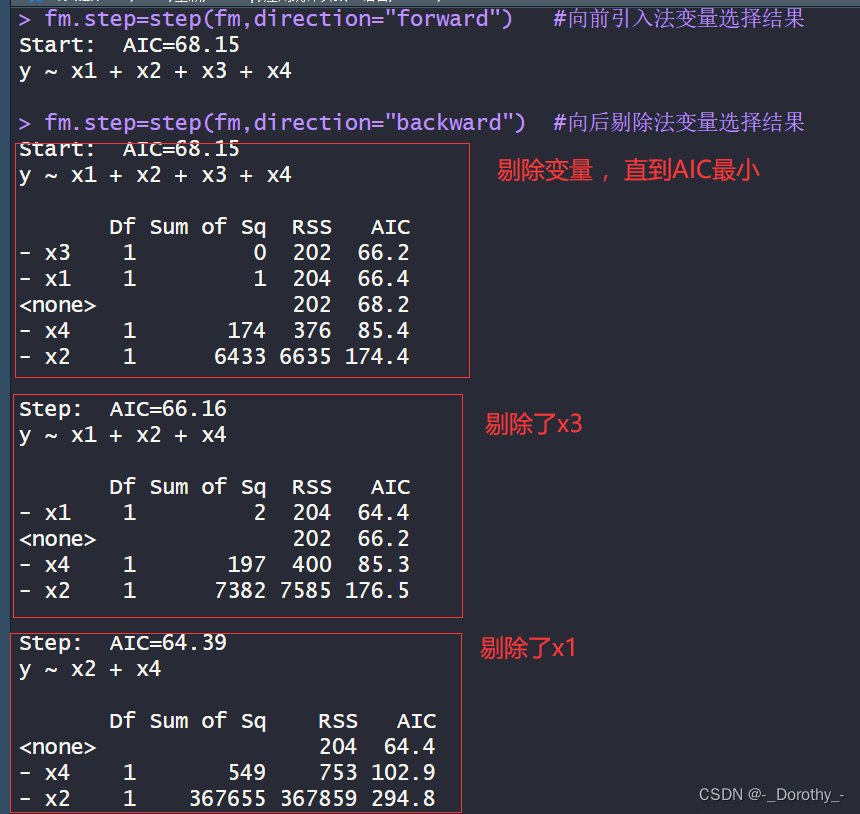
(2)逐步筛选法
这段输出展示了逐步筛选法(stepwise selection)的变量选择结果,结合了向前引入法和向后剔除法。
- 从一个包含所有自变量的模型开始。
- 首先,根据 AIC(Akaike Information Criterion)的准则,逐步剔除自变量,直到不再有改进(AIC值最小)为止。在这个过程中,自变量 x3 被剔除。
- 接着,在剔除了 x3 后,再根据 AIC 的准则逐步剔除自变量,直到不再有改进为止。在这个过程中,自变量 x1 被剔除。
- 最终的模型保留了自变量 x2 和 x4。
这些结果提供了一个平衡模型拟合度和模型复杂度的方案。最终的模型选择了 x2 和 x4 这两个自变量,因为它们能够在保持模型简洁的同时最大程度地解释因变量的变异。
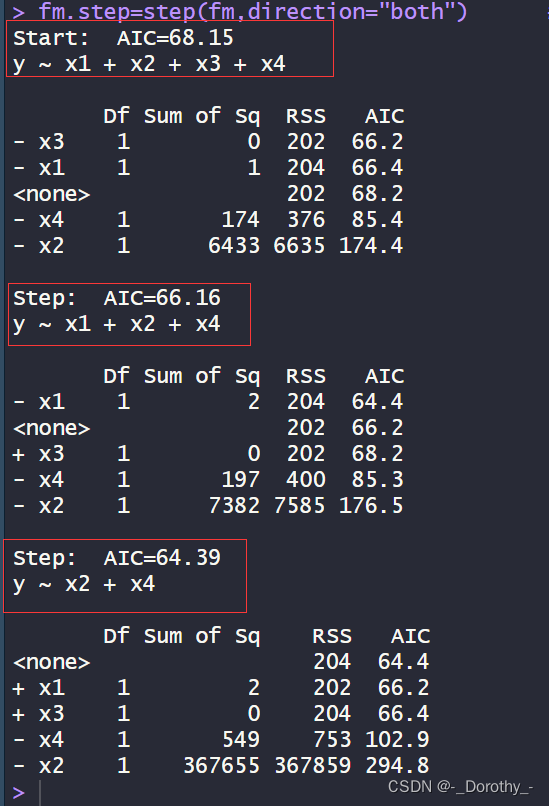
当模型含有不同变量时,对应的AIC值如下:
- 初始模型:y ~ x1 + x2 + x3 + x4,AIC=68.15
- 剔除了 x3:y ~ x1 + x2 + x4,AIC=66.16
- 剔除了 x1:y ~ x2 + x4,AIC=64.39
这些AIC值反映了模型的拟合程度和模型的复杂度之间的权衡。较小的AIC值表示模型对数据的拟合更好,同时考虑了模型的复杂度。
(3)模型拟合结果
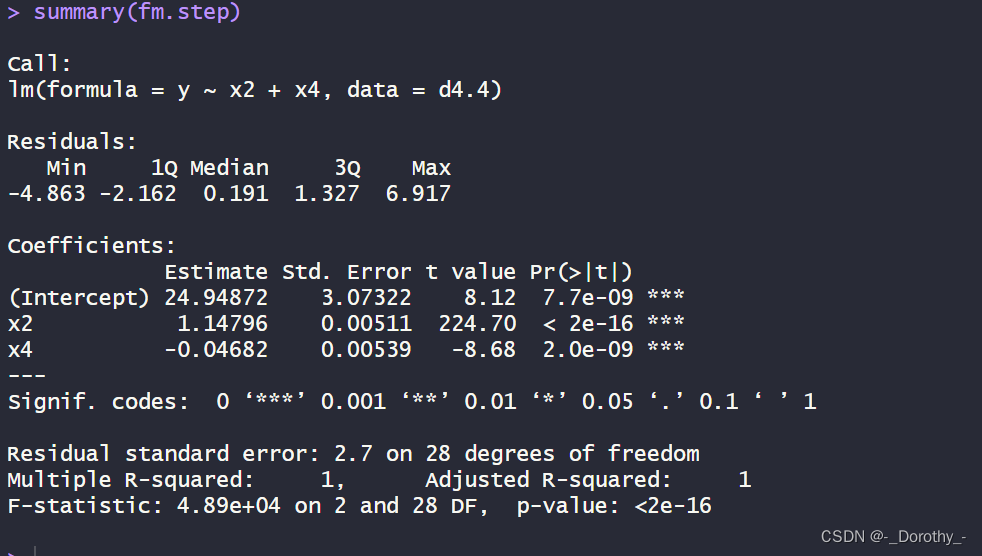
这段代码描述了一个多元线性回归模型的拟合结果,包括了模型的系数估计、p值、F检验等重要信息。
10、案例——财政收入的相关与回归分析
(1)case4数据
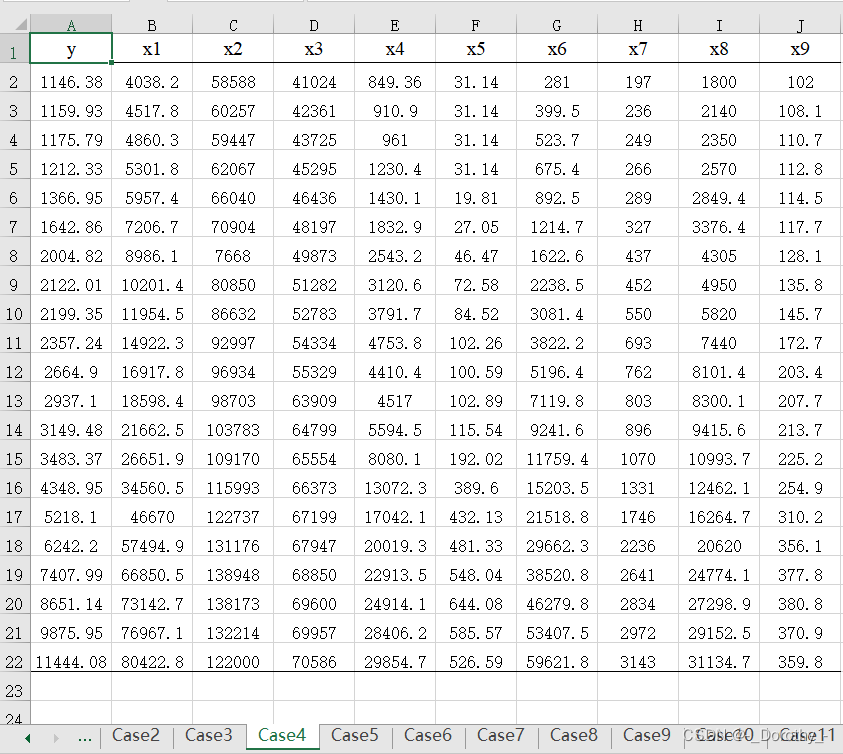
(2)代码
Case4=read.xlsx('adcase.xlsx','Case4');
summary(Case4)
cor(Case4) #相关分析
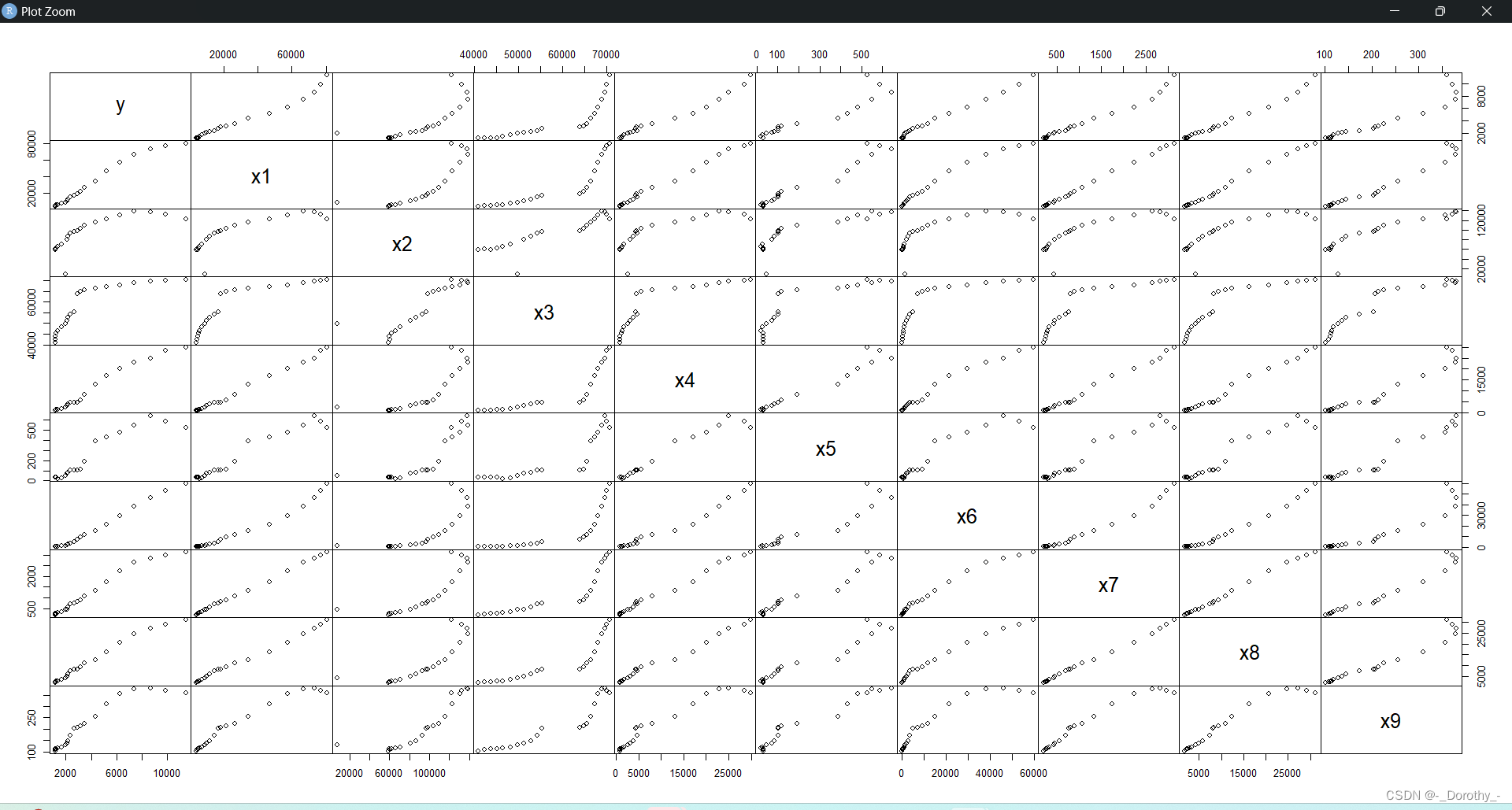
plot(Case4,gap=0) #矩阵散点图
msa.cor.test(Case4)
fm=lm(y~.,data=Case4);summary(fm)
sfm=step(fm);summary(sfm)
plot(Case4$y);lines(sfm$fitted)
(3)结果
(1)汇总统计
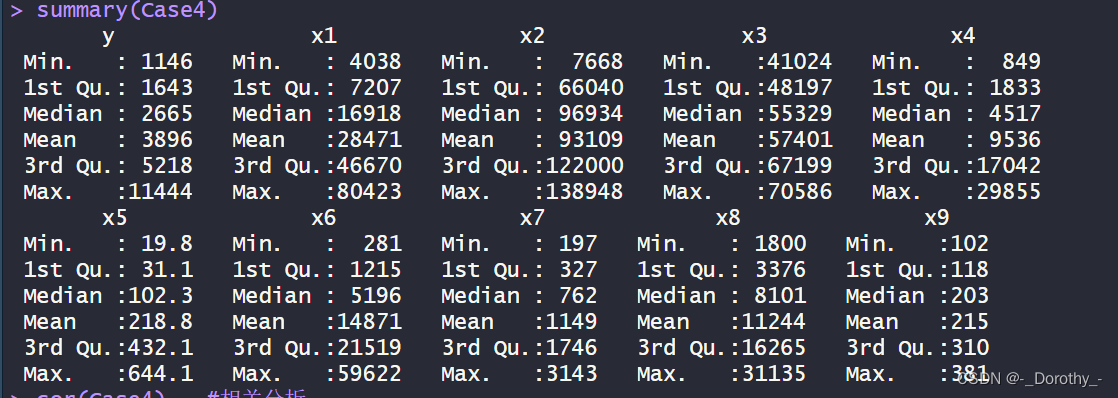
(2)相关分析
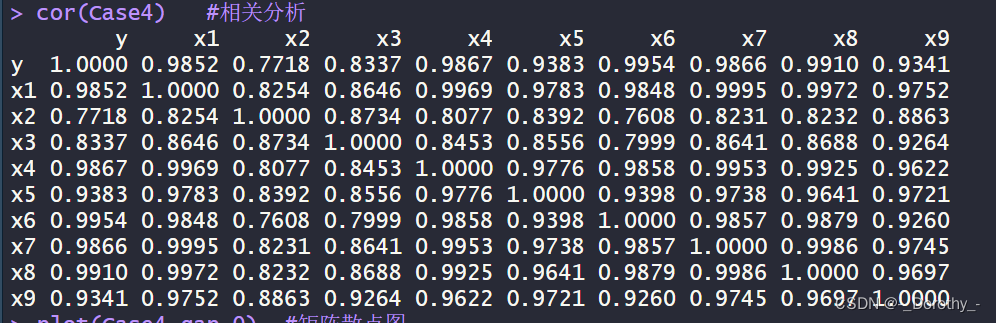
(3)矩阵散点图
(4)相关性检验
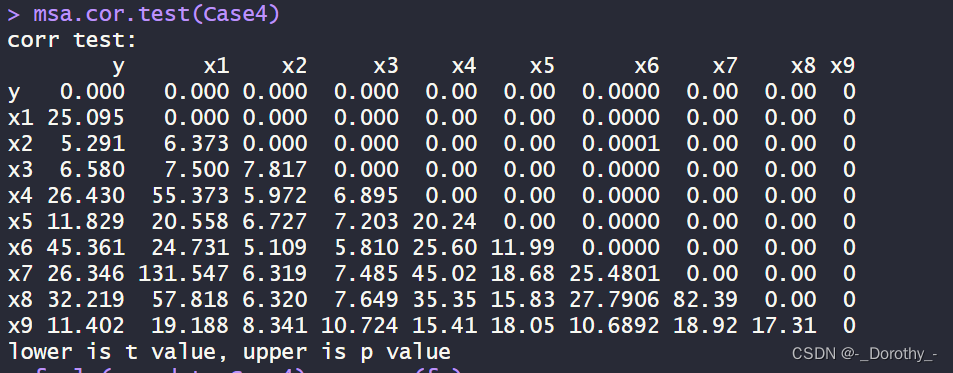
这段代码使用了 msa.cor.test 函数对 Case4 数据框中的变量进行了相关性检验,输出了相关性检验的结果。
-
目的:检验各个变量之间的相关性。
-
包含的信息:
- 相关系数(上三角矩阵):对角线上是每个变量自身的相关系数,其他位置是各个变量之间的相关系数。
- t值和p值(下三角矩阵):用于检验相关系数是否显著不等于0。
- t值表示检验统计量,用于判断相关系数是否显著不等于0。
- p值表示t检验的双侧p值,用于判断相关系数是否显著。
-
结论:
- t值较大或p值较小的相关系数意味着相关性较强且可能显著不等于0。
- t值和p值都为0的对角线位置表示每个变量自身与自身的相关系数,这是必然的。
通过这些信息,我们可以得出各个变量之间的相关性程度,并进一步分析各个变量之间的关联关系。
(5)线性回归分析
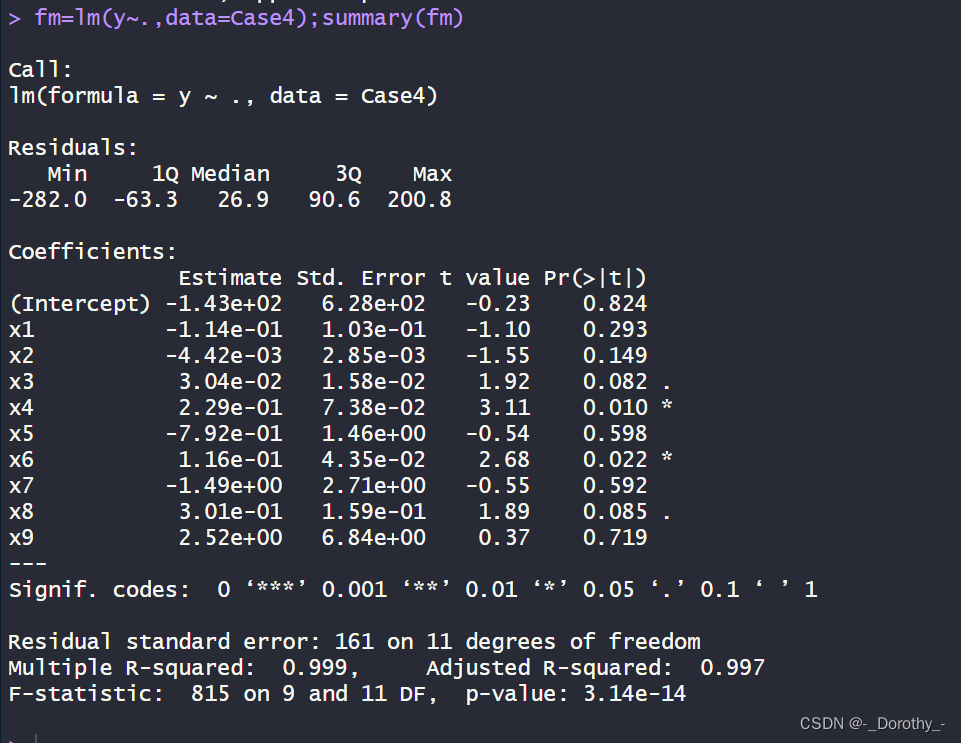
这段代码进行了线性回归分析,其中:
-
目的:通过最小二乘法拟合了一个线性模型,该模型用于预测因变量 y,该模型包含了自变量 x1 到 x9。
-
包含的信息:
- 模型系数(Estimate):对应每个自变量的系数估计值,表示自变量对因变量的影响程度。
- 标准误差(Std. Error):系数的标准误差,用于衡量估计系数的准确性。
- t值(t value):系数估计值除以标准误差的比值,用于检验系数是否显著不等于0。
- p值(Pr(>|t|)):t检验的双侧p值,用于判断系数是否显著不等于0。
- 残差标准误差(Residual standard error):残差的标准偏差,用于衡量模型对数据的拟合程度。
- 拟合优度(Multiple R-squared):表示模型对因变量的解释程度,值越接近1表示模型拟合程度越好。
- 调整后的拟合优度(Adjusted R-squared):考虑了模型中自变量数量的调整后的拟合优度,用于避免过度拟合的情况。
- F统计量(F-statistic):用于检验模型整体拟合优度的统计量。
- p值(p-value):F统计量的双侧p值,用于判断模型整体拟合优度是否显著。
-
结论:
- 模型整体拟合优度很高,Multiple R-squared为0.999,Adjusted R-squared为0.997,这表明模型能够很好地解释因变量的变异。
- 模型中有一些自变量的系数在统计上显著不等于0,如x4和x6,这些自变量可能对因变量有重要影响。
- 其他自变量的系数则不显著,如x1、x2、x5、x7、x8、x9,这些自变量可能对因变量的影响不显著。
(6)模型优化——逐步回归法
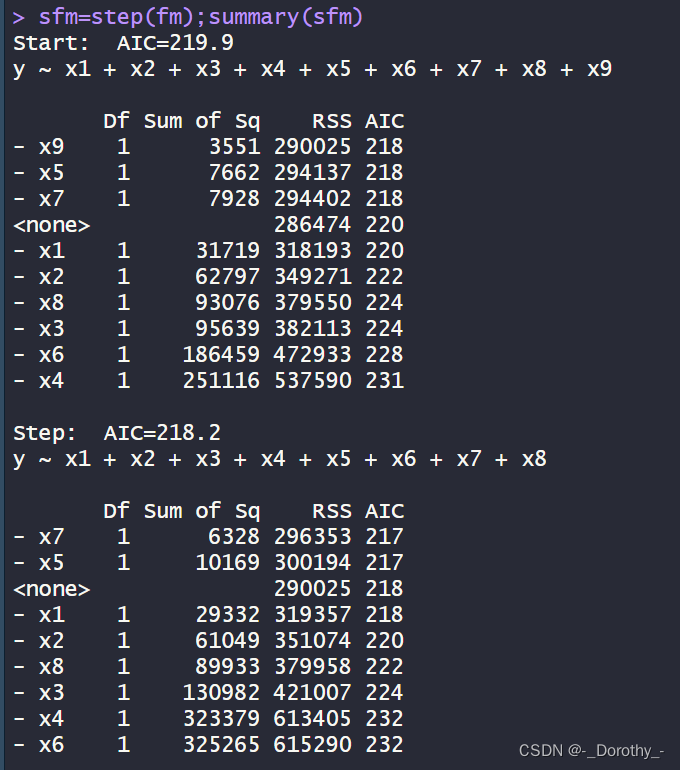
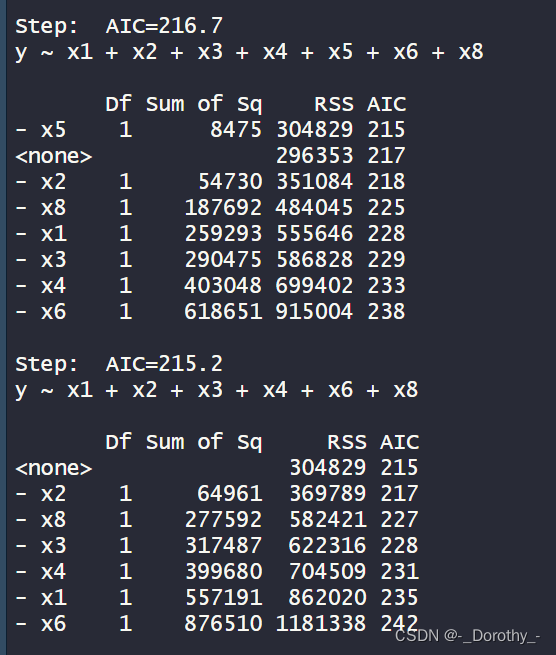
这段代码使用了逐步回归方法来选择模型,最终得到了一个相对较优的模型。逐步回归的目的是根据某个准则(如AIC)逐步添加或删除自变量,以得到一个在预测性能和模型复杂度之间达到平衡的模型。
-
模型选择过程:
- 初始模型包含了所有自变量 x1 到 x9。
- 逐步根据AIC值选择自变量:首先删除x9,然后删除x5和x7,最终得到了一个包含了x1、x2、x3、x4、x6和x8的最优模型。
- 每一步选择都会显示相应的自变量被删除后的模型的AIC值,以及相应的自变量的Sum of Sq、RSS和AIC值。
-
结论:
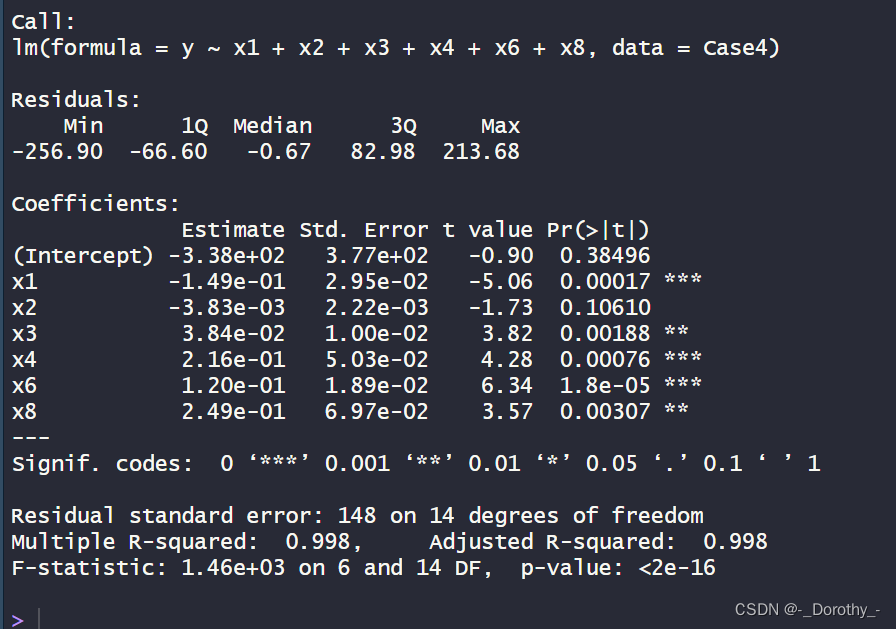
- 最终的模型包含了自变量 x1、x2、x3、x4、x6 和 x8。
- 这些自变量的系数估计值、标准误差、t值和p值显示在最终的模型汇总中。
- 可以用这个最终模型来预测因变量 y,且该模型在考虑了预测性能和模型复杂度后得到了一定的优化。
(7) 实际值和拟合值可视化
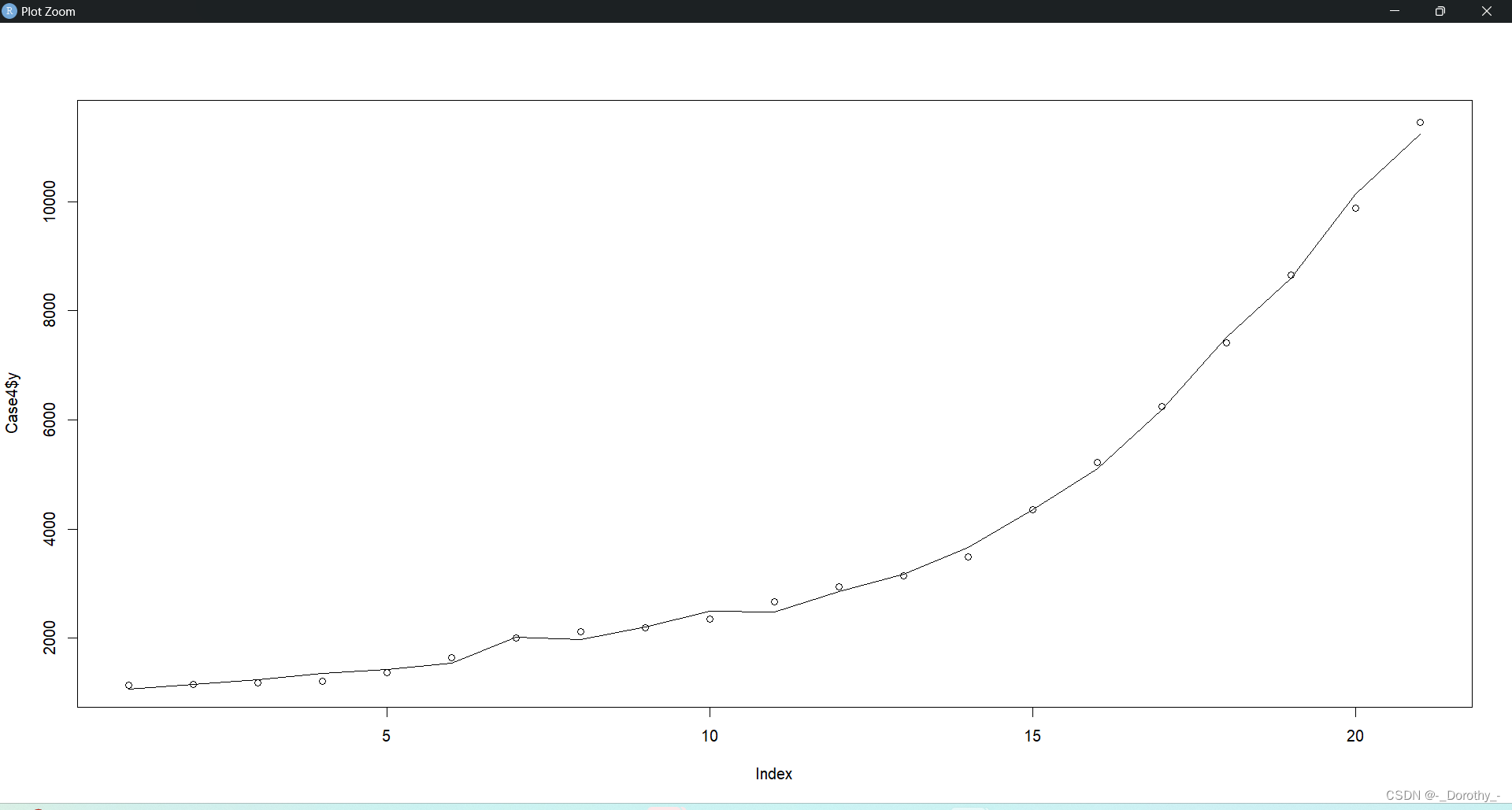
这段代码的目的是在同一张图上绘制实际观测值(Case4数据框中的y变量)和逐步回归模型(sfm)的拟合值。
-
plot(Case4$y):这个语句绘制了因变量 y 的实际观测值。在图中,每个点表示一个观测值。 -
lines(sfm$fitted):这个语句绘制了逐步回归模型 sfm 对应的拟合值。在图中,这些拟合值将作为一条曲线或折线,表示模型对每个观测值的预测值。
结论:
- 通过将实际观测值和模型拟合值绘制在同一张图上,可以直观地比较模型对数据的拟合程度。如果拟合值与实际观测值非常接近,则说明模型能够较好地解释数据的变异性。
- 如果拟合值与实际观测值有较大偏差,则可能需要重新评估模型的拟合情况或考虑改进模型。
这篇关于R语言学习—6—多元相关与回归分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







