每日OJ题_DFS爆搜深搜回溯剪枝⑧

每日OJ题_DFS爆搜深搜回溯剪枝⑧_力扣980. 不同路径 III

本文主要是介绍每日OJ题_DFS爆搜深搜回溯剪枝⑧_力扣980. 不同路径 III，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

力扣980. 不同路径 III

解析代码

力扣980. 不同路径 III

980. 不同路径 III

难度困难

在二维网格 grid 上，有 4 种类型的方格：

1 表示起始方格。且只有一个起始方格。
2 表示结束方格，且只有一个结束方格。
0 表示我们可以走过的空方格。
-1 表示我们无法跨越的障碍。

返回在四个方向（上、下、左、右）上行走时，从起始方格到结束方格的不同路径的数目。

每一个无障碍方格都要通过一次，但是一条路径中不能重复通过同一个方格。

示例 1：

输入：[[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
输出：2
解释：我们有以下两条路径：
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)

示例 2：

输入：[[1,0,0,0],[0,0,0,0],[0,0,0,2]]
输出：4
解释：我们有以下四条路径： 
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)

示例 3：

输入：[[0,1],[2,0]]
输出：0
解释：
没有一条路能完全穿过每一个空的方格一次。
请注意，起始和结束方格可以位于网格中的任意位置。

提示：

1 <= grid.length * grid[0].length <= 20

class Solution {
public:int uniquePathsIII(vector<vector<int>>& grid) {}
};

解析代码

可以用DP解决，但是这道题的DP是竞赛级别的，所以这里用爆搜的方法：对于四个方向，我们可以定义一个二维数组 next ，大小为 4 ，每一维存储四个方向的坐标偏移量。题目要求到达目标位置时所有无障碍方格都存在路径中，我们可以定义一个变量记录 num 当前状态中剩余的未走过的无障碍方格个数，则当我们走到目标地点时只需要判断 num 是否为 0 即可。在移动时需要判断是否越界。

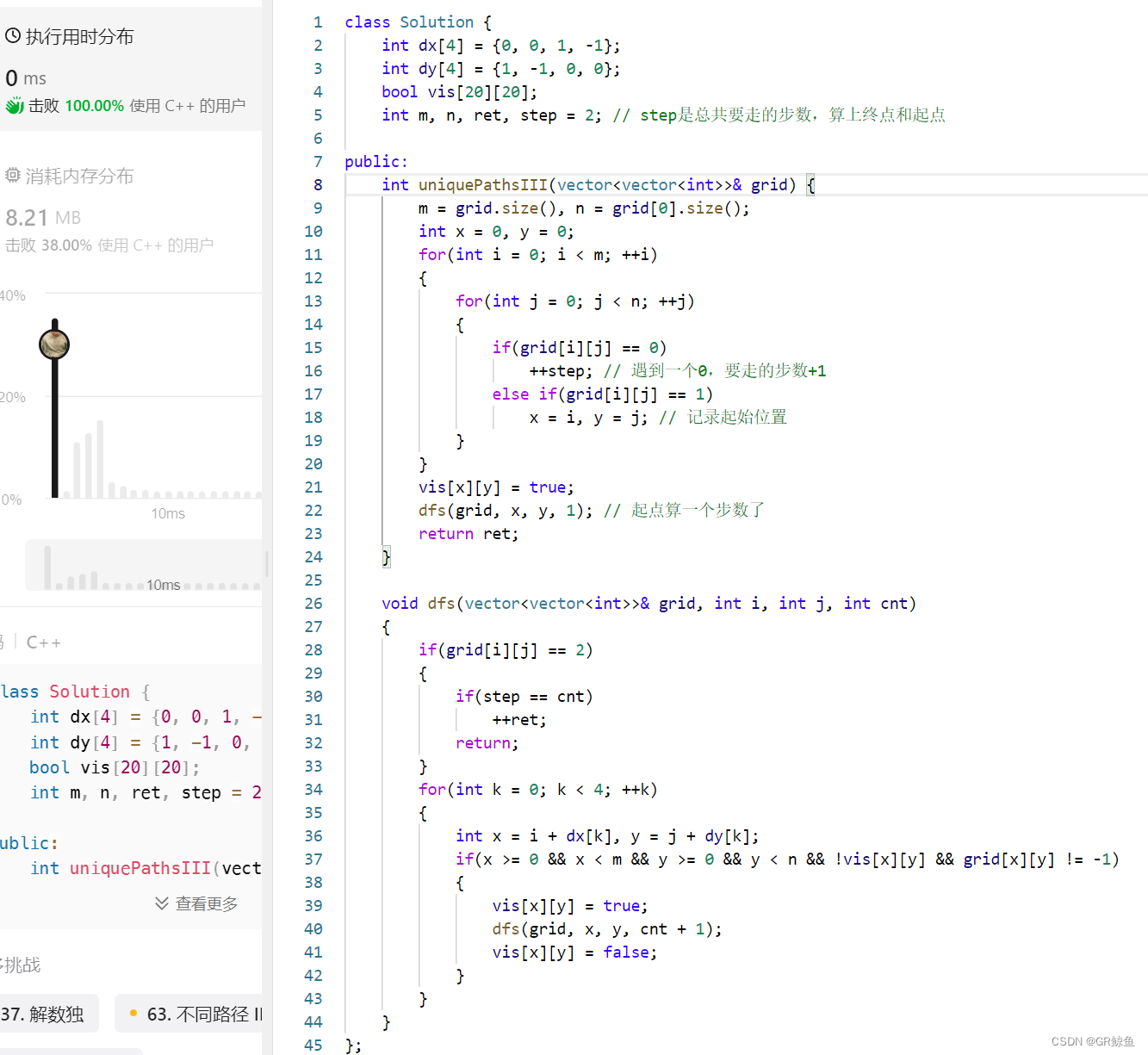
class Solution {int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};bool vis[20][20];int m, n, ret, step = 2; // step是总共要走的步数，算上终点和起点public:int uniquePathsIII(vector<vector<int>>& grid) {m = grid.size(), n = grid[0].size();int x = 0, y = 0;for(int i = 0; i < m; ++i){for(int j = 0; j < n; ++j){if(grid[i][j] == 0)++step; // 遇到一个0，要走的步数+1else if(grid[i][j] == 1)x = i, y = j; // 记录起始位置}}vis[x][y] = true;dfs(grid, x, y, 1); // 起点算一个步数了return ret;}void dfs(vector<vector<int>>& grid, int i, int j, int cnt){if(grid[i][j] == 2){if(step == cnt)++ret;return;}for(int k = 0; k < 4; ++k){int x = i + dx[k], y = j + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] != -1 && !vis[x][y]){vis[x][y] = true;dfs(grid, x, y, cnt + 1);vis[x][y] = false;}}}
};