2024五一杯：钢板最优切割路径问题（完整建模过程，仅供参考）

本文主要是介绍2024五一杯：钢板最优切割路径问题（完整建模过程，仅供参考），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

提高钢板下料切割过程中的工作效率，是模具加工企业降低成本和增加经济效益的重要途径，其中钢板切割的路径规划是钢板切割过程的一个关键环节。
钢板切割就是使用特殊的切割技术，基于给定的下料切割布局图纸对钢板进行加工。切割过程中设计切割路径至关重要，最优切割路径要满足空程最短的原则。

图1 钢板切割过程示意图

注：(1) 空程是指在切割设备所进行的一系列操作中不产生切割效果的水平运动路径(垂直运动路径不计入空程)；(2) 本题默认切割起始点均为右下角点(见各图所示)；(3) 本题下料切割布局图中的实线均为切割线。
请查阅相关资料，完成下列四个切割任务N1~N4：

问题一

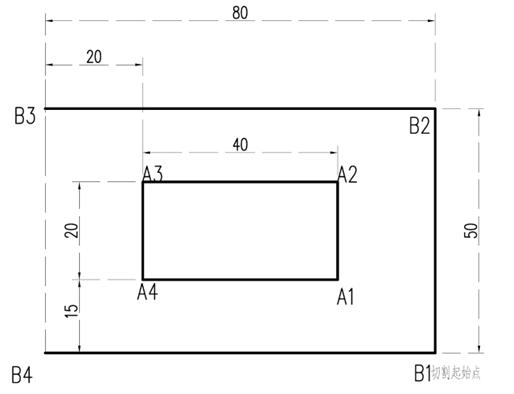
问题1：给定如图2所示的下料切割布局N1，其中B3-B4为钢板边界线，不用切割，B1为切割起始点。请建立数学模型，设计最优切割路径方案，并给出最优切割路径的空程总长度。

问题二

问题2：给定下料切割布局N2见图3，构件的外边界切割成上下对称的锯齿状，同时内部切割出四个半径为3的圆形和一个椭圆形。请根据下料切割布局N2的参数信息，建立数学模型，设计最优切割路径方案，并给出最优切割路径的空程总长度。

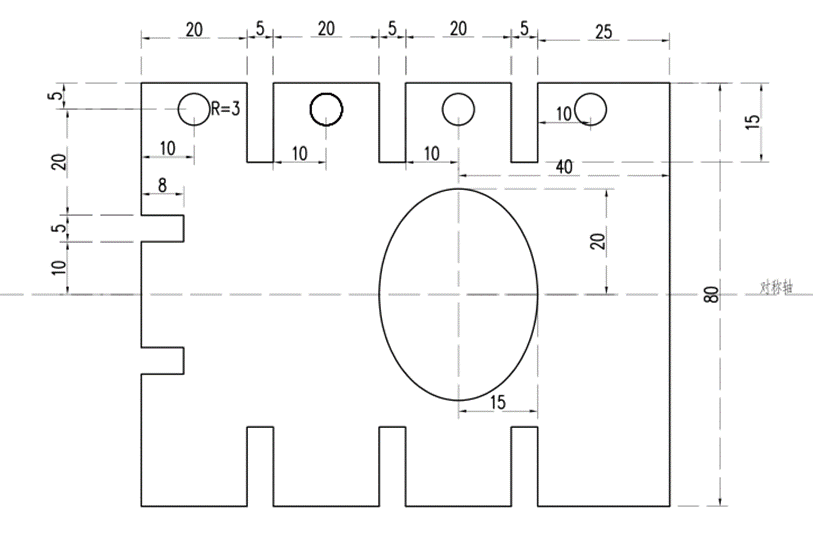
图3 含多个孔的下料切割布局N2

问题三

问题3：给定下料切割布局N3见图4。N3与N2相比，需要在椭圆中多切割出12个矩形件(它们在椭圆中的位置是对称分布的，左右相邻的两个矩形件的中心距离为6，上下相邻的两个矩形件的中心距离为5)。请建立数学模型，设计最优切割路径方案，并给出最优切割路径的空程总长度(要求椭圆内部的所有矩形件要先于椭圆切割)。

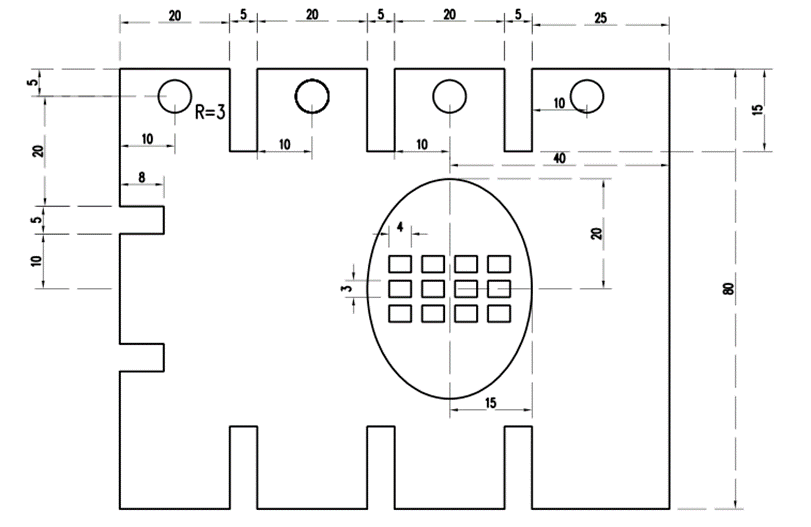
图4 含矩形件嵌套的下料切割布局N3

问题四

问题4：给定下料切割布局N4见图5，需要在椭圆中切割出4个矩形小零件。由于小零件尺寸较小，为防止小零件掉落，两个相邻的小零件之间需要采用“过桥”的方式，使得相邻零件连接成一个大尺寸零件，要求“过桥”与矩形小零件顶点的最短距离至少为1。“过桥”的宽度为2，且在空程计算中不可以忽略“过桥”的宽度。
请根据N4的具体情况，建立数学模型，确定“过桥”的数目和位置，设计最优切割路径方案，给出最优切割路径的空程总长度(要求切割起始点设计在钢板的右下角，N4中的小圆形切割件不考虑过桥问题)。

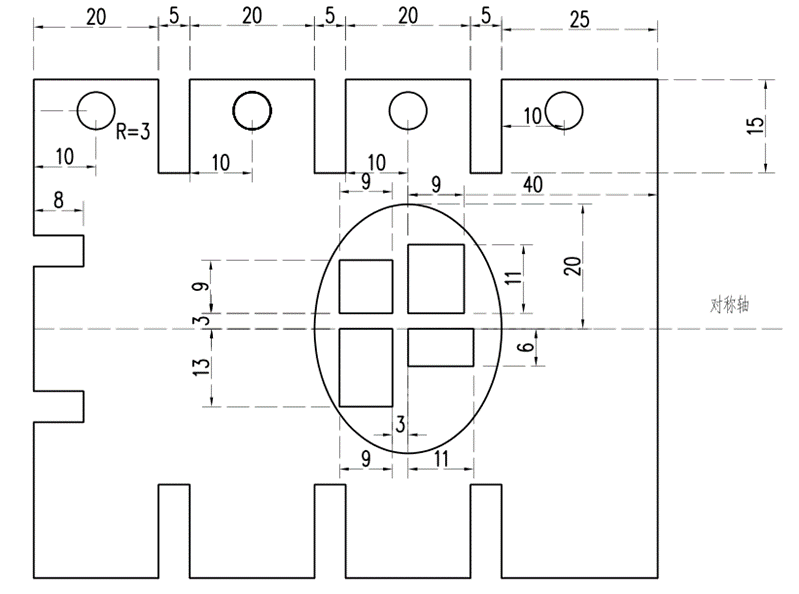
图5 需要添加过桥的嵌套矩形件套料图N4

题目解读

钢板切割是模具加工企业中常见的一个工序，目的是从大块钢板中切割出特定形状和尺寸的小块，用于后续的加工或制造过程。这个过程要求高效率和精确度以减少材料浪费，并提高生产效率。

空程（Idle Path）
这是指在切割过程中切割头进行的不进行切割的水平运动。题目特别指出，我们只关注水平方向上的空程，垂直方向的移动不计入空程。这主要是因为在许多切割设备中，水平移动的速度和控制与垂直移动不同，可能更耗时或更影响效率。

切割起始点：
题目说明了切割起始点总是位于钢板的右下角，即B1点。这意味着任何切割操作都从这一点开始，我们需要规划从这一点到第一次切割点的路径，以最小化空程。

下料切割布局图：
提供的图示展示了需要切割的内部矩形区域及其在整块钢板中的定位。内部矩形的四条边需要被完全切割，而外围的B3-B4线则是钢板的边界，不需要切割。(第一题为例）

切割路径的设计要求
目标是设计一条路径，从B1开始，切割完内部矩形的四条边，同时尽量减少没有切割效果的水平移动距离。理想的路径应该最小化空程，即在不进行切割的情况下的水平运动应尽可能短。（第一题为例）

规划：
基于上述的定义和要求，我们需要计算从B1（起始点）到A1（切割起始点）的水平距离，这是整个切割过程中唯一的空程部分，因为后续的动作都是围绕着内部矩形的边界进行的切割操作。

问题一建模过程

我们应该寻找一个直线路径，从起始点B1直接到切割点，这通常是两点之间最短的路径。

计算直线距离
从右下角B1到内部矩形的最近点（A4的左下角）：

1. B1的位置：右下角，坐标可以认为是 ((80, 0))。
2. A4左下角的位置：由于A4位于内部矩形左下角，其坐标为 (x = 15), (y = 20)。

因此，从B1到A4左下角的直线距离 (d) 可以通过勾股定理计算：

$$[d=\sqrt{(80-15{)}^2+(20-0{)}^2}=\sqrt{65^2+20^2}=\sqrt{4225+400}=\sqrt{4625}=10\sqrt{41}$$

切割方案

1. 直线移动：从B1 ((80, 0)) 直线移动到A4 ((15, 20))。
2. 切割顺序：
   • 从A4开始向上切割到A3（长度20mm）。
   • 从A3向右切割到A2（长度40mm）。
   • 从A2向下切割到A1（长度20mm）。
   • 从A1向左切割到A4（长度40mm）。

这样的切割方案利用了最短直线距离开始切割，符合减少空程的要求，并且完成了内部矩形的切割。

问题二建模过程

图纸详细解读
钢板的尺寸为80mm宽，50mm高。布局中包含了多个几何形状，包括几个小圆和一个大的椭圆形，以及钢板边缘的几个缺口。我们的任务是从右下角的切割起始点开始，计算到达第一个切割点的最短空程。

图形位置和尺寸

• 椭圆形：
  • 中心位于 ( (x, y) = (35, 25) )，长轴20mm，短轴15mm。
• 最右侧的小圆：
  • 半径3mm，中心位于 ( (x, y) = (80 - 5 - 3, 5 + 3) = (72, 8) )。

计算到第一个切割点的距离
由于切割起始点B1在右下角，我们考虑最右侧的小圆作为第一个切割目标。由于题目要求计算水平空程，我们应考虑从起始点B1到小圆的中心在垂直方向上的投影点的直线距离。

1. 起始点B1 的坐标是 (80, 0)。
2. 小圆中心点 的坐标是 (72, 8)。

计算直线距离
使用勾股定理计算B1到小圆中心的直线距离。从B1到小圆中心的水平和垂直距离分别是：

• 水平距离$$|80-72|=8\text{mm}$$
• 垂直距离$$|0-8|=8\text{mm}$$

因此，总的直线距离 ( d ) 是：
$$d=\sqrt{8^2+8^2}=\sqrt{64+64}=\sqrt{128}=8\sqrt{2}\text{ mm}$$

这条直线路径代表了从起始点到第一个切割点的最短路径，同时也是整个切割过程中唯一的空程。

问题三建模过程

为了解决问题三，我们需要规划一个从右下角B1开始的切割路径，该路径应包括首先切割大椭圆中的12个矩形件，然后再切割椭圆外围，同时确保路径的空程（没有切割效果的水平运动路径）最短。

加粗样式图纸详细解读

从图纸上可以看出，钢板尺寸为80mm宽，50mm高。大椭圆位于钢板中心偏右的位置，其长轴为20mm，短轴为15mm。椭圆中心大约位于 (x = 35 + 20/2 = 45, y = 15 + 15 = 30)。椭圆内部包含12个矩形，这些矩形按照一定的对称分布。

为了进一步细化问题三的解决方案，并确保我们提供最优切割路径，我们需要精确计算椭圆内部各个矩形中心的位置，从而确定从B1点到这些矩形的确切最短距离。同时，我们将验证切割顺序以确保遵循要求先切割所有椭圆内的矩形，然后切割椭圆。

图纸信息：
假设椭圆内部的12个矩形均匀分布，根据图纸信息：

• 椭圆中心位于 (45, 30)。
• 椭圆半长轴20mm，半短轴15mm。
• 矩形间的水平和垂直间距分别为6mm和5mm，不过具体矩形的尺寸没有详细标明。

计算假设
假设每个矩形的大小较小，我们可以初步估计靠近椭圆右下角的矩形中心位置。如果矩形相对较小，那么靠近椭圆右下角的矩形中心可以假设位于接近椭圆右下角的边缘。

最短路径计算
从B1（右下角，坐标(80, 0)）到靠近右下角的椭圆内矩形中心的位置可以假设为：

• 假定一个矩形位于椭圆的右下部分，考虑椭圆的几何中心和边界，可能的一个矩形中心位置是(65, 18)（这是一个估计位置，具体需要矩形的精确位置来确定）。

$$d=\sqrt{(80-65{)}^2+(18-0{)}^2}=\sqrt{15^2+18^2}=\sqrt{225+324}=\sqrt{549}$$

切割顺序和策略

1. 从靠近B1的矩形开始切割：开始于计算得出的最近矩形中心，顺序连接其他矩形中心。
2. 完成所有椭圆内部矩形后切割椭圆：由最后一个矩形移向椭圆边界，沿椭圆外边缘切割。

问题四建模过程

要为问题四建立数学模型并解决，我们首先需要完全理解切割要求、图纸布局、以及过桥的配置。然后，我们将确定最佳的切割路径，以最小化空程的长度。下面是这个过程的详细步骤。

1. 确定过桥的数量和位置

从图纸可以看到，四个矩形围绕一个椭圆排列。每个矩形的大小为3mm x 3mm，矩形之间的距离允许过桥连接。

• 过桥数量：由于矩形围绕椭圆布局，每两个相邻的矩形之间需要一个过桥。这样一共需要四个过桥。
• 过桥位置：
  • 两个水平过桥：连接左右相邻的两个矩形。
  • 两个垂直过桥：连接上下相邻的两个矩形。

过桥宽度为2mm，距离每个矩形的顶点至少为1mm。

2. 计算最优切割路径

确定最佳切割路径的关键是从起始点（右下角，坐标(80, 0)）到第一个切割点的直线距离最短。

• 首个切割点的选择：选择最接近起始点B1的矩形或过桥。从图中可以估算最接近的可能是位于椭圆右下方的矩形或其相邻的过桥。

3. 空程距离计算

假设最近的矩形位于椭圆的右下角，我们先估算该点的坐标。从椭圆中心(40, 25)到右下角矩形中心的大致位置可以是(40 + 6, 25 + 1.5) = (46, 26.5)。计算空程：

$$\text{空程}=\sqrt{(80-46{)}^2+(26.5-0{)}^2}=\sqrt{34^2+26.5^2}=\sqrt{1156+702.25}=\sqrt{1858.25}=43.1\text{ mm}$$

4. 切割路径设计

• 起始于：(46, 26.5)的矩形。
• 继续：连接相邻的矩形及过桥。
• 最后：切割椭圆外围。

5. 总结和实现

• 确定起始点和首个切割点，最小化从B1到首个切割点的空程。
• 连接所有矩形及过桥，保证切割的完整性和小矩形的安全。
• 最后切割椭圆外围，完成整体布局的切割。

这个模型满足了过桥的结构要求，最小化了空程，同时确保了小矩形在切割过程中的稳定性。通过这种方式，我们提供了一个系统的解决方案来高效地完成切割任务，同时保证切割件的质量和安全。

暂时没时间更新，以上过程仅供参考，并非最佳答案，有时间的同学调整优化下。更多的可以参考GPT站点：https://share.mosha.cloud/list

这篇关于2024五一杯：钢板最优切割路径问题（完整建模过程，仅供参考）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---