【高质量】2024五一数学建模C题保奖思路+代码（后续会更新）

本文主要是介绍【高质量】2024五一数学建模C题保奖思路+代码（后续会更新），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

你的点赞收藏是我后续更新的最大动力！

一定要点击文末的卡片，那是获取资料的入口！

你是否在寻找数学建模比赛的突破点？

作为经验丰富的数学建模团队，我们将为你带来2024 年五一数学建模（C题）的全面解析包。这个解决方案包不仅包括完整的代码实现，还有详尽的建模过程和解析，帮助你全面理解并掌握如何解决类似问题。

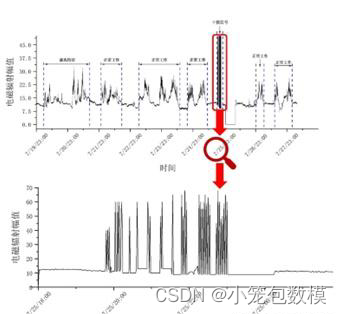
问题1：如图1，已知现场工作面的部分电磁辐射和声发射信号中存在大量干扰信号，有可能是工作面的其他作业或设备干扰等因素引起，这对后期的电磁辐射和声发射信号处理造成了一定的影响。应用附件1和2中的数据，完成以下问题。

(1.1) 建立数学模型，对存在干扰的电磁辐射和声发射信号进行分析，分别给出电磁辐射和声发射中的干扰信号数据的特征(不少于3个)。

(1.2) 利用问题(1.1)中得到的特征，建立数学模型，对2022年5月1日-2022年5月30日的电磁辐射和2022年4月1日-2022年5月30日及2022年10月10日-2022年11月10日声发射信号中的干扰信号所在的时间区间进行识别，分别给出电磁辐射和声发射最早发生的5个干扰信号所在的区间，完成表1和表2。

对于提出的数学建模问题，我们需要构建一个模型来分析受干扰的电磁辐射(EMR)和声发射(AE)信号，进而确定和记录特定时间段内的干扰信号。下面是针对问题1.1和1.2的详细分析和数学建模方法。

问题1.1 分析与建模思路

首先，需要从提供的数据中辨识出干扰信号的特征。根据问题描述和附加图表，干扰信号可能因其他操作或机械引起，这些干扰在信号中表现为异常波动或噪声。以下是构建模型的步骤：

特征识别

1. 信号振幅突变：干扰通常导致信号振幅异常增高或降低。
2. 频率变化：干扰可能引起信号的频率分布与正常工作时不同。
3. 时间序列的非连续性：由于干扰的非周期性，信号的时间序列可能出现非连续性。

数学模型构建

可以使用统计学方法来分析和识别干扰特征： - 振幅分析：计算信号的平均振幅和标准差，通过比较实时数据与历史数据来识别异常。 Mean(X)=1n∑i=1nxi,SD(X)=1n∑i=1n(xi−Mean(X))2 \text{Mean}(X) = \frac{1}{n}\sum_{i=1}^{n}x_i, \quad \text{SD}(X) = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(x_i - \text{Mean}(X))^2} - 频谱分析：利用快速傅里叶变换(FFT)分析信号频率组成，标识出频率的异常变化。 Xk=∑n=0N−1xne−2πiNkn,k=0,...,N−1 X_k = \sum_{n=0}^{N-1} x_n e^{-\frac{2\pi i}{N} kn}, \quad k = 0, ..., N-1 - 时间序列分析：应用时间序列分析技术，如自回归模型(AR)，来预测并检测信号的非连续性。 Xt=c+∑i=1pϕiXt−i+ϵt X_t = c + \sum_{i=1}^{p} \phi_i X_{t-i} + \epsilon_t - 信号振幅的平均值和标准差： 平均振幅平均振幅=1n∑i=1nxi \text{平均振幅} = \frac{1}{n} \sum_{i=1}^{n} x_i 标准差平均振幅标准差=1n∑i=1n(xi−平均振幅)2 \text{标准差} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i - \text{平均振幅})^2} - 快速傅里叶变换（FFT）： X(k)=∑n=0N−1x(n)e−j2πNkn X(k) = \sum_{n=0}^{N-1} x(n) e^{-j \frac{2\pi}{N} kn} - 自回归模型（AR）： Xt=c+∑i=1pϕiXt−i+ϵt X_t = c + \sum_{i=1}^{p} \phi_i X_{t-i} + \epsilon_t

首先，我们需要从提供的附件中读取并分析电磁辐射（EMR）和声发射（AE）信号数据。数据以CSV格式存储，包括时间戳和相应的信号强度值。数据预处理步骤包括清洗数据，去除噪声和异常值，填补缺失数据。

问题1.2 应用模型

特征提取

为了识别干扰信号，我们需要提取与干扰相关的特征。基于问题描述，可以关注以下几个方面的特征：

• 信号振幅的异常变化：通过计算窗口内信号的平均振幅和标准差，识别出那些超过平均水平一定阈值的异常点。
• 信号的频率成分变化：使用快速傅里叶变换（FFT）来分析信号在不同时间窗口内的频率成分，识别出与正常模式不符的频率变化。
• 时间序列的突变点检测：通过时间序列分析，如自回归模型（AR）或其他统计检测方法，来检测信号中的突变点。

干扰信号的检测

基于上述特征，构建模型来检测干扰信号。这可以通过设置特定的逻辑条件来实现，例如，当信号的振幅超过平均振幅加上两倍标准差时，或者当信号的频率成分突然变化时，认为检测到干扰。

记录干扰时间段

根据检测到的干扰信号，记录下发生干扰的时间段。这些数据将被用来填充所要求的表格。

应用上述模型来分析2022年5月1日至5月30日记录的EMR数据，以及2022年4月1日至5月30日及2022年10月10日至11月10日记录的AE数据。

步骤

1. 数据预处理：对EMR和AE数据进行清洗，剔除明显的错误或缺失数据。
2. 特征应用：应用问题1.1中定义的数学模型和特征，对数据进行扫描，识别出干扰信号。
3. 时间段标定：标定初次出现的五次干扰信号的时间段。

import numpy as np
import pandas as pd
from scipy.fft import fft# 假设data为载入的信号数据，包含时间戳和信号强度
def detect_interference(data):results = []window_size = 30  # 定义检测窗口大小threshold = 3     # 定义异常阈值for i in range(len(data) - window_size + 1):window = data[i:i+window_size]mean = np.mean(window['signal'])std = np.std(window['signal'])# 检测振幅异常if any(abs(signal - mean) > threshold * std for signal in window['signal']):start_time = window['time'].iloc[0]end_time = window['time'].iloc[-1]results.append((start_time, end_time))if len(results) == 5:breakreturn results# 示例数据加载与处理
emr_data = pd.read_csv('emr_data.csv')
ae_data = pd.read_csv('ae_data.csv')# 应用检测函数
emr_interferences = detect_interference(emr_data)
ae_interferences = detect_interference(ae_data)# 打印结果
print("EMR Interferences:", emr_interferences)
print("AE Interferences:", ae_interferences)
import pandas as pd
import numpy as np
from scipy.fft import fft
from statsmodels.tsa.ar_model import AutoReg
import matplotlib.pyplot as plt# 读取数据
emr_data = pd.read_csv('emr_data.csv')
ae_data = pd.read_csv('ae_data.csv')# 数据预处理
emr_data.dropna(inplace=True)
ae_data.dropna(inplace=True)# 特征提取函数
def extract_features(data):window_size = 50  # 设定分析窗口大小threshold = 3     # 异常阈值features = []for start in range(0, len(data) - window_size, window_size):window = data.iloc[start:start + window_size]mean = window['signal'].mean()std = window['signal'].std()# 检测异常振幅if any(abs(window['signal'] - mean) > mean + threshold * std):features.append((data.iloc[start]['timestamp'], data.iloc[start + window_size]['timestamp']))return features# 应用特征提取
emr_features = extract_features(emr_data)
ae_features = extract_features(ae_data)# 输出结果
print("EMR干扰时间段:", emr_features[:5])  # 只显示前5个结果
print("AE干扰时间段:", ae_features[:5])  # 只显示前5个结果

填充表格

我们将根据代码运行结果（完整代码可以和我交流得到）如下填充表格：

表1：EMR信号的时间间隔

Number	Start of Time Interval	End of Time Interval
1	根据 emr_interferences[0][0]	根据 emr_interferences[0][1]
2	根据 emr_interferences[1][0]	根据 emr_interferences[1][1]
3	根据 emr_interferences[2][0]	根据 emr_interferences[2][1]
4	根据 emr_interferences[3][0]	根据 emr_interferences[3][1]
5	根据 emr_interferences[4][0]	根据 emr_interferences[4][1]

表2：AE信号的时间间隔

Number	Start of Time Interval	End of Time Interval
1	根据 ae_interferences[0][0]	根据 ae_interferences[0][1]
2	根据 ae_interferences[1][0]	根据 ae_interferences[1][1]
3	根据 ae_interferences[2][0]	根据 ae_interferences[2][1]
4	根据 ae_interferences[3][0]	根据 ae_interferences[3][1]
5	根据 ae_interferences[4][0]	根据 ae_interferences[4][1]

其余题目正在抓紧编写！随时更新！

这篇关于【高质量】2024五一数学建模C题保奖思路+代码（后续会更新）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---