一文学会回溯算法解题技巧

本文主要是介绍一文学会回溯算法解题技巧，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

上文我们学习了深度优先搜索和广度优先搜索，相信大家对这两者的算法有了比较清楚的认识，值得一提的，深度优先算法用到了回溯的算法思想，这个算法虽然相对比较简单，但很重要，在生产上广泛用在正则表达式，编译原理的语法分析等地方，很多经典的面试题也可以用回溯算法来解决，如八皇后问题，排列组合问题，0-1背包问题，数独问题等，也是一种非常重要的算法。

本文将会从以下几个方面来讲述回溯算法，相信大家看了肯定有收获！

1. 什么是回溯算法
2. 回溯算法解题通用套路
3. 经典习题讲解

什么是回溯算法

回溯算法本质其实就是枚举，在给定的枚举集合中，不断从其中尝试搜索找到问题的解，如果在搜索过程中发现不满足求解条件 ，则「回溯」返回，尝试其它路径继续搜索解决，这种走不通就回退再尝试其它路径的方法就是回溯法，许多复杂的，规模较大的问题都可以使用回溯法，所以回溯法有「通用解题方法」的美称。

回溯算法解题通用套路

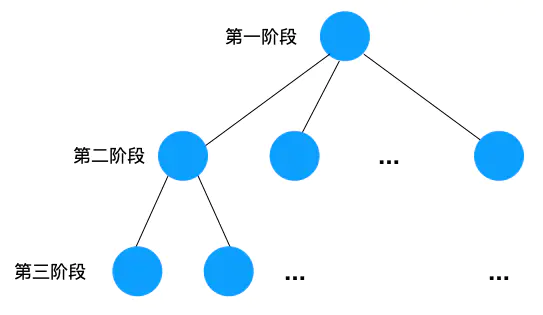
为了有规律地求解问题，我们把问题分成多个阶段，每个阶段都有多个解，随机选择一个解，进入下一个阶段，下一个阶段也随机选择一个解，再进入下一个阶段...

image

每个阶段选中的解都放入一个 「已选解集合」 中，并且要判断 「已选解集合」是否满足问题的条件（base case）,有两种情况

1. 如果「已选解集合」满足问题的条件，则将 「已选解集合」放入「结果集」中，并且「回溯」换个解再遍历。
2. 如果不满足，则「回溯」换个解再遍历

根据以上描述不难得出回溯算法的通用解决套路伪代码如下:

 

function backtrace(已选解集合,每个阶段可选解) {if (已选解集合满足条件) {结果集.add(已选解集合);return;}// 遍历每个阶段的可选解集合for (可选解 in 每个阶段的可选解) {// 选择此阶段其中一个解,将其加入到已选解集合中已选解集合.add(可选解)// 进入下一个阶段backtrace(已选解集合,下个阶段可选的空间解)// 「回溯」换个解再遍历已选解集合.remove(可选解)}
}

通过以上分析我们不难发现回溯算法本质上就是深度优先遍历，它一般解决的是树形问题（问题分解成多个阶段，每个阶段有多个解，这样就构成了一颗树），所以判断问题是否可以用回溯算法的关键在于它是否可以转成一个树形问题。

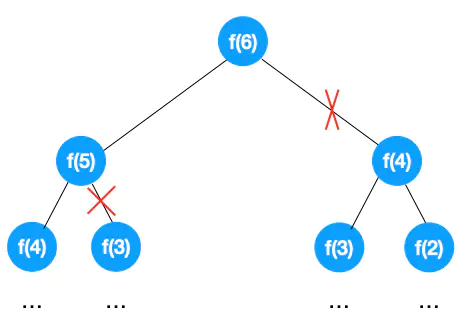
另外我们也发现如果能缩小每个阶段的可选解，就能让问题的搜索规模都缩小，这种就叫「剪枝」，通过剪枝能有效地降低整个问题的搜索复杂度！之前我们在一文学会递归解题中求解斐波那契问题时就用到了减枝的技巧，使问题的空间大大减少（如下图示）

image

综上，我们可以得出回溯算法的基本套路如下：

1. 将问题分成多个阶段，每个阶段都有多个不同的解，这样就将问题转化成了树形问题，这一步是问题的关键！如果能将问题转成树形问题，其实就成功了一半，需要注意的是树形问题要明确终止条件，这样可以在 DFS 的过程中及时终止遍历，达到剪枝的效果
2. 套用上述回溯算法的解题模板，进行深度优先遍历，直到找到问题的解。

只要两个步骤，是不是很简单！接下来我们套用以上的解题模板来看看怎么使用以上回溯算法解题套路来解几道经典的问题。

经典习题讲解

一、全排列

给定数字 1，2，3，求出 3 位不重复数字的全排列

1、将问题转为树形结构

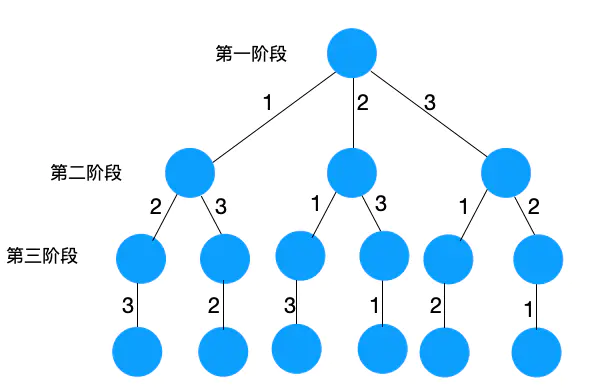
由于求的是 3 位数的全排列，所以问题分解为 3 个阶段，第一个阶段可以选 1，2，3 三个解，如果第一阶段选完数字后，第二个阶段可以选另外 2 个解，同理第三个阶段也可以选择剩下一个解。树形结构如下：

image

2、套用上述回溯算法的解题模板，进行深度优先遍历，直到找到问题的解

代码如下:

 

public class Solution {/*** 结果集*/private static List<String> RESULT = new ArrayList<>(10);/*** 参与全排列的数字*/private static List<Integer> NUMS = Arrays.asList(1, 2, 3);/*** 遍历当前阶段的解* @param selectedNums   已选解集合* @param selectableNums 可选的解集合*/public static void permutation(List<Integer> selectedNums, List<Integer> selectableNums {// 满足条件，加入结果集if (selectedNums.size() == NUMS.size()) {RESULT.add(Arrays.toString(selectedNums.toArray()));return;}// 遍历每个阶段的可选解集合for (int i = 0; i < selectableNums.size(); i++) {Integer num = selectableNums.get(i);// 去除不符合条件的解，减枝if (selectedNums.contains(num)) {continue;}// 选择当前阶段其中一个解selectedNums.add(num);// 选完之后再进入下个阶段遍历permutation(selectedNums, selectableNums);// 回溯,换一个解继续遍历selectedNums.remove(num);}}public static void main(String[] args) {List<Integer> selectedNums = new ArrayList<>();permutation(selectedNums, NUMS);System.out.println(Arrays.toString(RESULT.toArray()));}
}

为了让大家更好地理解上述代码，我一步步地画出了每个阶段的解题图解，对照着以上代码看相信大家应该能看明白

 

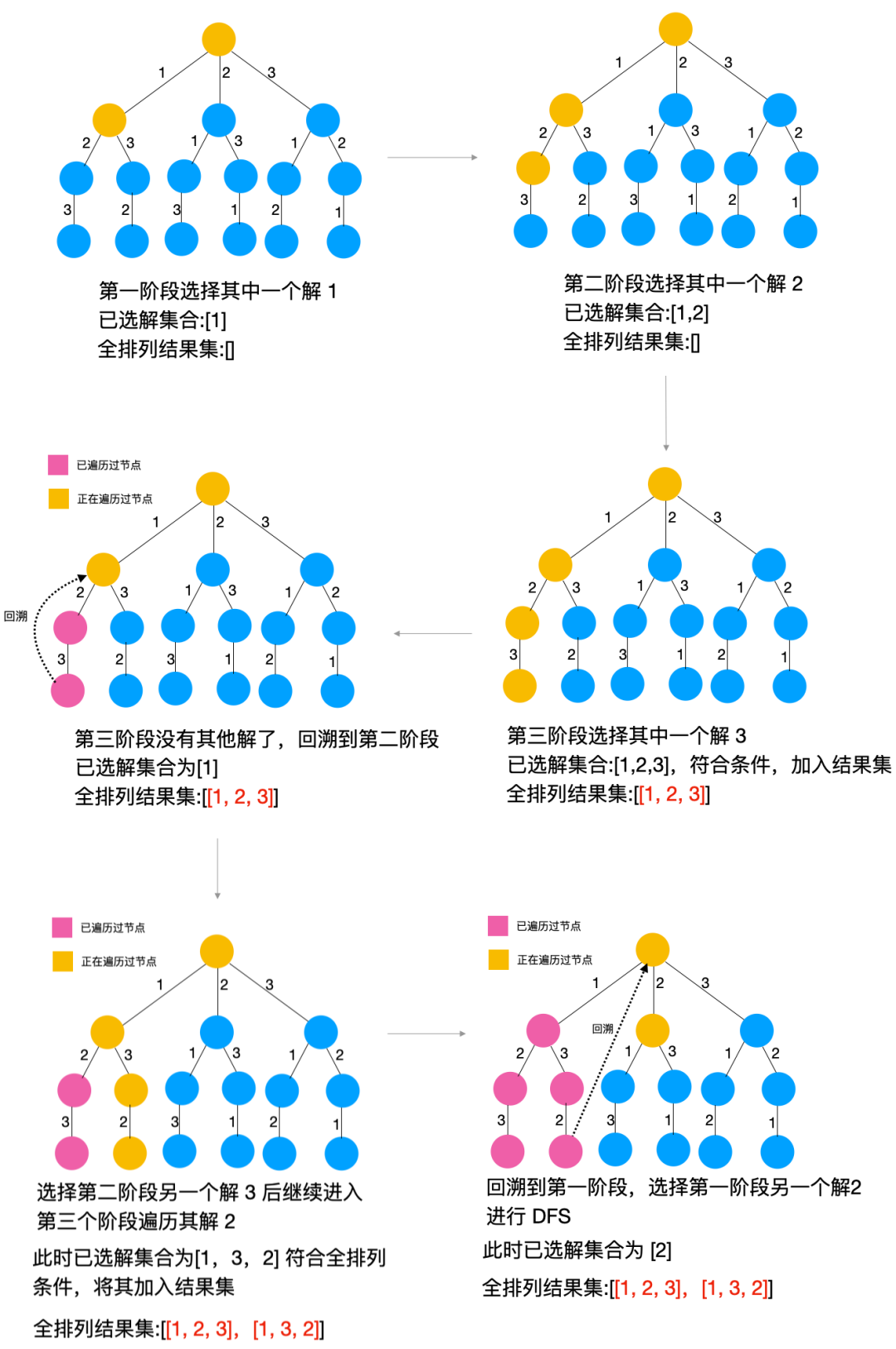
二、0-1背包问题

这里介绍一下一种比较简单的背包问题：

有一个背包，背包总的承载重量是 Wkg。现在我们有 n 个物品，每个物品的重量不等，并且不可分割。我们现在期望选择几件物品，装载到背包中。在不超过背包所能装载重量的前提下，如何让背包中物品的总重量最大？假设这 n 个物品的质量分别 3kg, 4kg, 6kg, 8kg，背包总的承载重量是 10kg。

套用回溯算法解题思路

1、将问题转为树形结构

由于有 n 个物品，所以问题可以分解成 n 个阶段，第一个阶段可以有 n 个物品可选，第二个阶段有 n-1 个物品可选,,,,,,最后一个阶段有 1 个物品可选，不难画出以下递归树

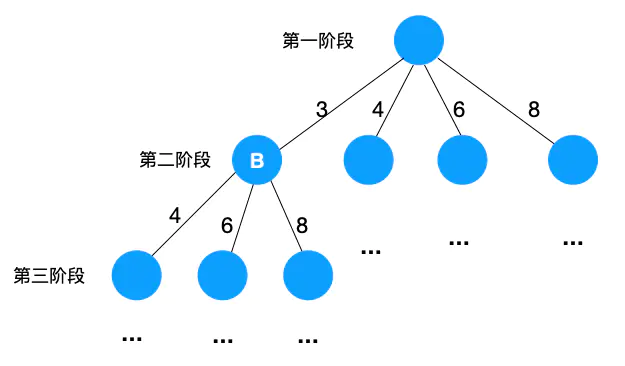
image

既然能转成树形结构，那我们进入步骤 2

2、套用上述回溯算法的解题模板，进行深度优先遍历，直到找到问题的解

需要注意的，进行 DFS 的终止条件是什么呢，显然是所选物品质量（遍历的节点）和大于等于背包质量，稍加变形不难得出以下代码

 

public class Solution {/*** 结果集*/private static Integer RESULT = 0;/*** 背包最大承载质量*/private static Integer KNAPSACK_MAX_WEIGHT = 10;/*** 现有背包*/private static List<Integer> WEIGHTS = Arrays.asList(3, 4, 6, 8);/*** 遍历当前阶段的解** @param selectedWeights  已选解集合* @param selectableWeight 可选的解集合*/public static void knapsack(List<Integer> selectedWeights, List<Integer> selectableWeight) {{// 求已选物品的总重量int sumOfWeights = selectedWeights.stream().mapToInt(Integer::intValue).sum();if (sumOfWeights == KNAPSACK_MAX_WEIGHT) {RESULT = Math.max(RESULT, sumOfWeights);return;} else if (sumOfWeights > KNAPSACK_MAX_WEIGHT) {// 如果已选物品的总重量超过背包最大承受质量，则要把最后一个选择的物品移除，再求质量和selectedWeights.remove(selectedWeights.size() - 1);sumOfWeights = selectedWeights.stream().mapToInt(Integer::intValue).sum();RESULT = Math.max(RESULT, sumOfWeights);return;} else {RESULT = Math.max(RESULT, sumOfWeights);}}// 遍历每个阶段的可选解集合for (int i = 0; i < selectableWeight.size(); i++) {Integer num = selectableWeight.get(i);// 去除不符合条件的解，减枝if (selectedWeights.contains(num)) {continue;}// 选择子节点的其中一个解selectedWeights.add(num);// 选完之后再进行 dfsknapsack(selectedWeights, selectableWeight);// 「回溯」换个解再遍历selectedWeights.remove(num);}}public static void main(String[] args) {List<Integer> selectedNums = new ArrayList<>();knapsack(selectedNums, WEIGHTS);System.out.println("result = " + RESULT);}
}

可以看到套用模板我们又轻松解决了0-1背包问题，可能有人会说以上问题比较简单，接下来我们来看看如何用上模板来解八皇后问题。

3、八皇后

老读者对八皇后问题应该并不陌生，之前我们在位运算的文章中详细地讲解了如何用位运算来求解八皇后问题，当时也说了，用位运算来求解，是效率最高的，其实八皇后问题也可以用我们的回溯算法来求解，只不过不是那么高效而已，不过可读性更好。

来简单回顾上什么是八皇后问题。

八皇后问题：8x8 的棋盘，希望往里放 8 个棋子（皇后），每个棋子所在的行、列、对角线都不能有另一个棋子

如下所示是 8 皇后问题的一种放法。

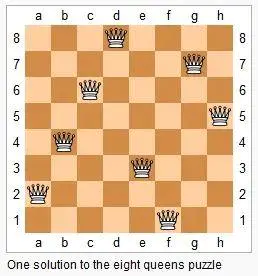
image

1、将问题转为树形结构

对于 N 皇后问题，问题可以分解为 N 个阶段， 第一个阶段即第一行有 N 个解（N 列中的做生意一个解）， 第二阶段（第二行）由于受第一行限制（皇后所在列，斜线不能放），解肯定是少于 N 个解，它的解视第一行所放皇后位置而定,... ，第 N 个阶段的解受前面 N-1 个阶段解的影响。N 皇后树形结构如下

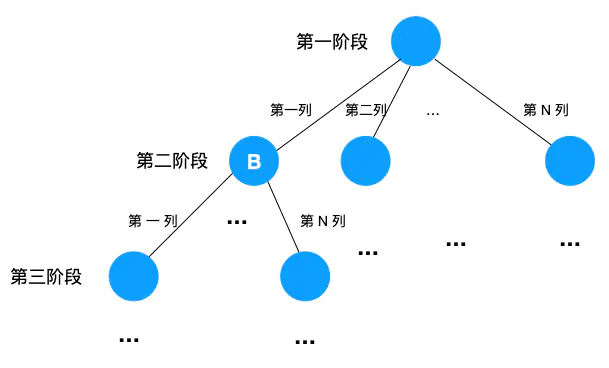
image

2、套用上述回溯算法的解题模板，进行深度优先遍历，直到找到问题的解

套用以上模板时，注意终止条件与每个阶段（每一行）所选解是否合法（剪枝）即可。注意看下 queenSettle 的方法，这是套用我们的回溯算法解题模板所得出来的，其他方法都是在此模板上进行添砖加瓦而已。

 

public class Solution {private static Integer N = 8;/**** @param selectedColumns 已选解集合,下标表示行,值表示queen存储在哪一列* @param row             可选的空间解,第 n 行可选*/public static void queenSettle(int[] selectedColumns, int row) {// 终止条件if (row > N - 1) {// 说明前 N 行都已经都选完皇后了，printQueens(selectedColumns);return;}for (int i = 0; i < N; i ++) {// 剔除不合法的格子if (!isValid(row, i, selectedColumns)) {continue;}// 选择子节点（当前行）其中一个解selectedColumns[row] = i;// 选完之后再进入下个阶段的（下一行）遍历queenSettle(selectedColumns, row + 1);// 回溯,换一个解继续 dfs，回溯时要把回溯节点的解移除selectedColumns[row] = -1;}}/*** 判断相应的格子放置皇后是否OK* @param row* @param column* @param selectedColumns* @return*/private static boolean isValid(int row, int column, int[] selectedColumns) {//判断row行column列放置是否合适int leftup = column - 1, rightup = column + 1;for (int i = row-1; i >= 0; --i) { // 逐行往上考察每一行if (selectedColumns[i] == column) return false; // 第i行的column列有棋子吗？if (leftup >= 0) { // 考察左上对角线：第i行leftup列有棋子吗？if (selectedColumns[i] == leftup) return false;}if (rightup < 8) { // 考察右上对角线：第i行rightup列有棋子吗？if (selectedColumns[i] == rightup) return false;}--leftup; ++rightup;}return true;}public static void main(String[] args) {int[] selectedColumn = new int[N];// 从第 0 行开始 DFSqueenSettle(selectedColumn, 0);}private static void printQueens(int[] result) { // 打印出一个二维矩阵for (int row = 0; row < 8; ++row) {for (int column = 0; column < 8; ++column) {if (result[row] == column) System.out.print("Q ");else System.out.print("* ");}System.out.println();}System.out.println();}
}

可以看到八皇后这么复杂的问题套用以上的解题模板也被我们轻松解决了！

总结

使用回溯算法解题的关键是把问题分成多阶段，每个阶段都有相应的解，于是就把问题转成了树形问题，转成树形问题后，剩下的只需要套用上文总结的解题模板即可，尤其需要注意的是，当遍历当前阶段解的时候，可以根据之前阶段的解作「剪枝」操作，这样使问题的搜索规模变小，有效降低了问题的复杂度。

巨人的肩膀

• https://mp.weixin.qq.com/s/nMUHqvwzG2LmWA9jMIHwQQ 回溯算法详解
• https://time.geekbang.org/column/article/74287 回溯算法：从电影《蝴蝶效应》中学习回溯算法的核心思想

作者：码农小光
链接：https://www.jianshu.com/p/8c8aad53ce38
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

这篇关于一文学会回溯算法解题技巧的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---