【Leetcode 377】组合总和 Ⅳ —— 动态规划

本文主要是介绍【Leetcode 377】组合总和 Ⅳ —— 动态规划，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

377. 组合总和 Ⅳ

给你一个由 不同 整数组成的数组nums，和一个目标整数target。请你从nums中找出并返回总和为target的元素组合的个数。

题目数据保证答案符合 32 位整数范围。

示例 1：

输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同的组合。

示例 2：

输入：nums = [9], target = 3
输出：0

题目分析

经典动态规划问题，更多案例可见 Leetcode 动态规划详解

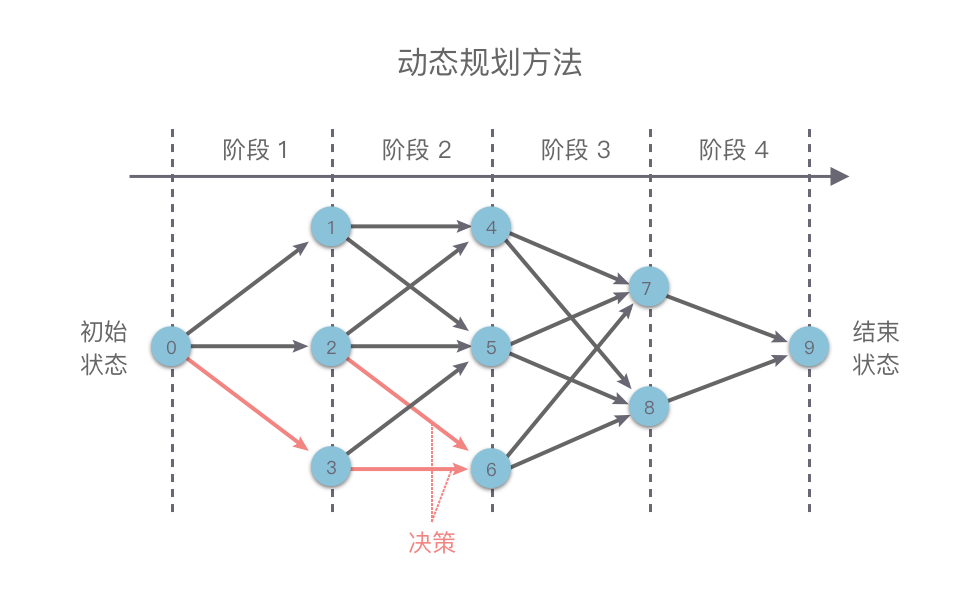
我们可以使用动态规划解决本题，解题思路：

1. 状态定义：
   • dp[i] 表示总和为i的元素组合的个数
2. 状态转移方程：对于总和为i的组合，我们可以选择一个数num，然后在剩余的总和为i - num的情况下选择其他数，所以总的组合个数为dp[i - num]

$$dp[i][j]=\sum _{num=0}^{i}dp[i-num]$$

3. 初始状态dp[0] = 1即空集，最终答案为 dp[target]

动态规划一般用于求解具有重叠子问题和最优子结构的问题，例如最长公共子序列、背包问题、最短路径等。重叠子问题指的是在求解问题的过程中，多次用到相同的子问题，最优子结构指的是问题的最优解可以通过子问题的最优解来构造

class Solution {public int combinationSum4(int[] nums, int target) {int[] dp = new int[target + 1];dp[0] = 1;for (int i = 1; i <= target; i++) {for (int num : nums) {if (i >= num) {dp[i] += dp[i - num];}}}return dp[target];}
}

这篇关于【Leetcode 377】组合总和 Ⅳ —— 动态规划的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---