本文主要是介绍DS进阶:二叉搜索树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、概念
二、搜索二叉树相关操作
1.查找
2.插入
3.删除(难点)
第一类:
第二类:
第三类:
三、性能分析
一、概念
二叉搜索树,又称二叉排序树,它或者是一颗空树,也是具有一下特征:
1.若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
2.若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
因此,二叉搜索树中没有重复的元素。
3.它的左右子树也分别为二叉搜索树
其次,二叉搜索树进行中序遍历会得到一个升序的序列。
如图:
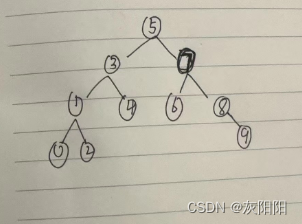
二、搜索二叉树相关操作
搜索二叉树的基本结构和普通二叉树没有任何区别:

1.查找
对于给定的元素int val
在搜索二叉树root(先假设root是已经创建好的二叉搜索树)中进行查找:
//方法也很简单,只要依照二叉搜索树右子树永远大于双亲节点,左子树永远小于双亲节点的性质即可public TreeNode findNode(int val){if(root==null)return null;//如果树是空的,就无法寻找了TreeNode cur=root;//cur用来遍历整棵树while(cur!=null){if(cur.val<val){//往右边走cur=cur.right;}else if(cur.val>val){//往左边走cur=cur.left;}else{//cur.val==val就是要找的节点return cur;}}return null;//在这颗树中没有找到,直接返回空}2.插入
二叉搜索树的插入有点不同,想要在二叉搜索树中插入一个元素:
那么必须在叶子节点下面插入,才能够保证结构特点不发生改变。
以下面这颗二叉搜索树为例:

如果要插入一个val=10的结点:

如果要插入一个val=-1的结点:

上述的插入,都是在叶子节点操作的,且最后插入完成之后,仍然是二叉搜索树。
至于如何找对叶子结点,请看下面代码以及注释:
public boolean insertNode(int val) {//插入成功返回真,否则假TreeNode newNode = new TreeNode(val);//先创建好一个结点if (root == null) {root = newNode;//首次插入return true;//直接返回}TreeNode cur = root;//用来遍历树,找到合适的叶子结点TreeNode parent = null;//用来记录cur的双亲结点//插入的结点必须也要满足二叉搜索树的性质,所以如果val大于根结点的值,就往右树走,反之往左树走while (cur != null) {parent = cur;if (cur.val < val) {cur = cur.right;} else if (cur.val > val) {cur = cur.left;} else {//cur.val==valreturn false;//这种情况是不允许的,因为二叉搜索树,每个元素各不相同}}//出循环之后,cur=null parent就是正确的叶子结点//还是依照二叉搜索树的性质,来判断位置if(parent.val<val){parent.right=newNode;}else{//parent.val>valparent.left=newNode;}//注意下面这种写法是不行的,因为cur已经等于空了,如果parent左右都空,那么就可能出现插入位置错误
/* if (cur == parent.right) {parent.right = newNode;} else {//cur==parent.leftparent.left = newNode;}*/return true;}3.删除(难点)
设待删除的结点为cur
待删除的结点的双亲结点为parent
想要删除某一个结点,而又不破坏二叉搜索树的结构,依据不同的情况,分为三大类:
第一类:cur.left==null(cur.right可以是空,也可以不是空)
第二类:cur.right==null(cur.left可以是空,也可以不是空)
注意:前两类有一个重叠情况,就是cur.left和cur.right都是空的情况,不过都不影响,往下看就知道了
第三类:cur.right!=null&&cur.left!=null
第一类:
cur.left==null(cur.right可以是空,也可以不是空)
删除val=7的结点:

在第一类中,cur.left肯定是空的,要安全删除,接可以直接这样:

这样不就大功告成了吗?
我们再回头看看这个val=8的结点,如果这个结点是空,即原先的条件是cur.left==null&&cur.right==null是不是也可以用这个逻辑,显然也是可以的嘛,parent.right=null呗。
所以前文说即使前两类有所重叠但是其实没有影响。
第二类:
cur.right==null(cur.left可以是空,也可以不是空)
第二类和第一类,不说一摸一样,完全相同肯定是有的 ƪ(˘⌣˘)ʃ
删除val=6的结点:
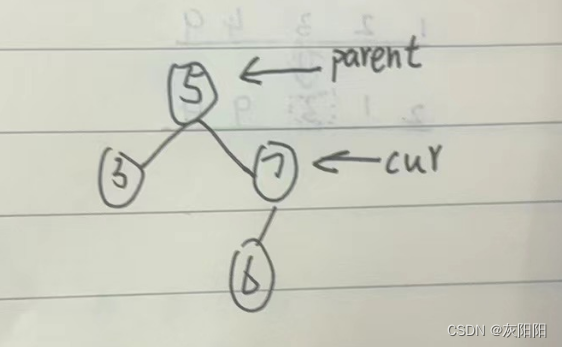
因为是第二类,所以cur.right肯定是空嘛
parent.right=cur.left就可以咯,就是第一类的左右颠倒:
显然,val=6的结点可有可无,反正我的parent.right指向的就是你,管你是啥呢。
第三类:
cur.right!=null&&cur.left!=null
第三类相对来讲有点特殊,不过他转来转去,用的还是是前面两类的方法。
此话怎讲?
活动一下僵硬的嘎吱窝,俺娓娓道来:
删除val=7 的结点:

第一步:
找到cur结点右子树中,val值最小的结点,命名为:replace
第二步:
cur.val和replace.val进行互换:
要删除的是val=7这个结点,您看这图眼熟不眼熟。
这不就是第一类中的情况吗?
没错,此时我们成功的把问题,转化为了前面两类的其中之一了。
第三步:
使用第一类中的逻辑,最终实现删除。
注意:
有时候,替换完可能是第一类的情况,也可能是第二类的情况,但是思路都一样的呢。
转化为代码:
public boolean remove(int val){//首先要找到cur(要删除的结点)和parent(cur的双亲结点)TreeNode cur=root;TreeNode parent=null;while(cur!=null){//一直遍历这颗树去寻找parent=cur;if(cur.val<val){//往右边,找大的cur=cur.right;}else if(cur.val>val){//往左边,找小的cur=cur.left;}else{//cur.val==val//找到了的情况/*下面代码嵌套的比较多,封装一个方法来实现*/_remove(parent,cur);return true;}}//程序到这,说明要删除的结点都没有找到,直接返回假return false;}private void _remove(TreeNode parent,TreeNode cur){if(cur.left==null){//第一类if(parent.left==cur){//要先判断双亲结点哪一个子树是curparent.left=cur.right;}else{//parent.right==curparent.right=cur.right;}}else if(cur.right==null){//第二类if(parent.left==cur)parent.left=cur.left;else parent.right=cur.left;}else{//要删除的结点左右两个子树都不为空------>第三类/* 对于第三类*///第一步:在cur的右子树中找到最小值的结点TreeNode min=cur.right;TreeNode minDad=null;//min的双亲结点while(min.left!=null){//一直遍历cur右子树的左树,因为左子树永远更小minDad=min;min=min.left;}//出了这个循环,叶子结点已经找到了//第二步:叶子节点和要要删除的结点的val进行交换cur.val=min.val;//反正min结点要交换,更改cur结点的val就可以了//第三步:以min结点作为要删除的结点,执行第一类逻辑即可完成if(min==minDad.left){//要先判断双亲结点的那个子结点是要删除的结点minDad.left=min.right;//min.left一定是空的,因为我们找的就是最小的叶子节点}else{//min==minDad.rightminDad.right=min.right;//min.left一定是空的,因为我们找的就是最小的叶子节点}}}三、性能分析
插入和删除操作都必须先查找,所以查找效率代表了二叉搜索树中各个操作的性能。
由于二叉搜索树储存元素的特点,查找效率就和这颗二叉树的深度有关系,结点越深,比较次数就越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
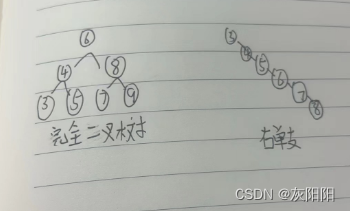
显而易见:
最优情况下,二叉搜索树是完全二叉树,比较次数为:logN
最差情况下,二叉搜索树是单分支树,比较次数为:N
为了优化搜索二叉树的效率,由此在二叉搜索树的基础上,诞生了AVL树,和红黑树,等等。这里就不展开了,留在下一篇在介绍吧。
完
这篇关于DS进阶:二叉搜索树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








