本文主要是介绍24.4.28(板刷dp,拓扑判环,区间dp+容斥算回文串总数),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
星期一:
昨晚cf又掉分,小掉不算掉
补ABC350 D atc传送门

思路:对每个连通块,使其成为一个完全图,完全图的边数为 n*(n-1)/2 , 答案加上每个连通块成为完全图后的边数,最后再减去m即可
代码如下(dfs实现:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
int m;
vector<int>ve[N];
int co[N],cnt[N];
inline void dfs(int u,int c){ //染色if(co[u]!=-1) return ;co[u]=c;for(auto v:ve[u]) dfs(v,c);
}
void solve(){cin >> n >> m;for(int i=1;i<=m;i++){int a,b; cin >> a >> b;ve[a].push_back(b);ve[b].push_back(a);}memset(co,-1,sizeof co);for(int i=1;i<=n;i++) dfs(i,i);for(int i=1;i<=n;i++) cnt[co[i]]++; //计算每个连通块的点的个数ll ans=0;for(int i=1;i<=n;i++){if(!cnt[i]) continue;ans+=1ll*cnt[i]*(cnt[i]-1)/2; //此连通块成为完全图后的边数}ans-=m; //减去已有的m条边cout << ans;
}代码如下(并查集实现:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
int m;
int fa[N],sum[N];
inline int fnd(int x){return fa[x]==x?x:fa[x]=fnd(fa[x]);
}
void solve(){cin >> n >> m;for(int i=1;i<=n;i++) fa[i]=i,sum[i]=1;for(int i=1;i<=m;i++){int u,v; cin >> u >> v;u=fnd(u),v=fnd(v);if(u==v) continue;fa[v]=u;sum[u]+=sum[v];}ll ans=0;for(int i=1;i<=n;i++){if(fa[i]!=i) continue;ans+=1ll*sum[i]*(sum[i]-1)/2;}cout << ans-m;
}补cf round940 C: cf传送门

思路:dp【i】表示消去 i 个行列的方案数
当棋子的摆放结果相同时,棋子的摆放顺序没有意义,所以考虑一行一行的放,dp【i】可以由 dp【i-1】放在(i,i)转移,除此位置,第 i 行剩余 i - 1个位置将会消去两行列,且颜色不同也算不同方案,于是得到状态转移方程如下
初始状态dp【0】和dp【1】都为1
代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
ll k;
ll dp[N];
void solve(){cin >> n >> k;while(k--){int r,c; cin >> r >> c;if(r==c) n--;else n-=2;}dp[0]=dp[1]=1;for(int i=2;i<=n;i++)dp[i]=dp[i-1]+2*(i-1)*dp[i-2],dp[i]%=mod;cout << dp[n] << "\n";
}星期二:
补cf round940 D(异或难题 cf传送门

思路:先把条件转化一下,f ( x,z) 异或 ay 大于 f ( x,z),再转化一下,ay 被多少区间穿过且该区间异或和在 ay最高位 为0,这样异或后此位为1,无论低位如何变化都大于原数
cnt【i】【j】表示到 i 为止,有多少点的前缀异或和在二进制 j 位上为1,两区间在二进制 j 位上异或和相同,异或后结果为0, 统计后用乘法原理计算
代码如下:
const int N=2e5+10,M=210;
const int mod=1e9+7;
ll n;
int a[N];
int cnt[N][33];
void solve(){cin >> n;for(int i=1,s=0;i<=n;i++){cin >> a[i];s^=a[i]; //前缀异或和for(int j=32;j>=0;j--)cnt[i][j]=cnt[i-1][j]+(s>>j&1);}ll ans=0;for(int i=1;i<=n;i++){int k=__lg(a[i]); //ai的最高位ans+=1ll*cnt[i-1][k]*(cnt[n][k]-cnt[i-1][k]);ans+=(i-cnt[i-1][k])*(n-i+1-(cnt[n][k]-cnt[i-1][k]));}cout << ans << "\n";
}记录下午比赛一题: cf传送门

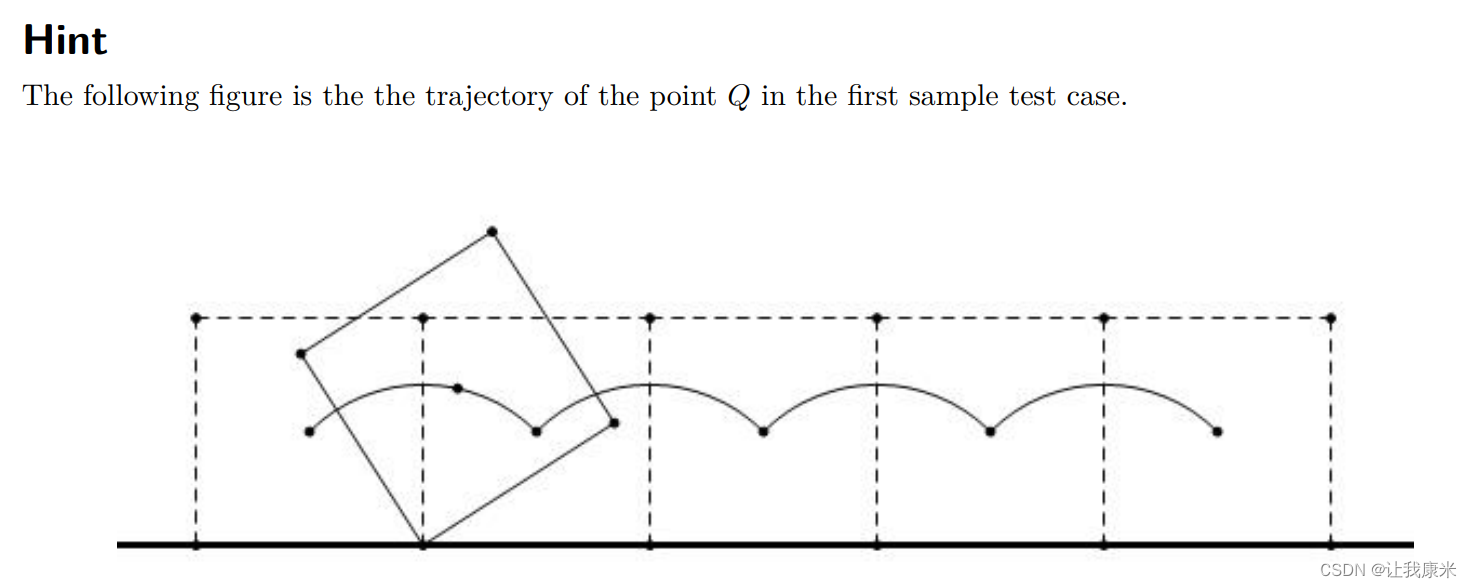
题意:一多边形在地上滚一圈,问图形内一点的轨迹长度
思路:每次转动,轨迹为一扇形,角度为触地角的补角,半径为q点到触地点的距离,使用数学公式计算即可
代码如下:
ll n;
pair<double,double> q[55];
double xx,yy;
double ans;
double cal(int idx){double x1,y1,x2,y2,x3,y3;if(idx==1) x1=q[n].first,y1=q[n].second;else x1=q[idx-1].first,y1=q[idx-1].second;if(idx==n) x3=q[1].first,y3=q[1].second;else x3=q[idx+1].first,y3=q[idx+1].second;x2=q[idx].first,y2=q[idx].second;double r=sqrt((xx-x2)*(xx-x2)+(yy-y2)*(yy-y2)); //扇形的半径 rdouble a=sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));double b=sqrt((x2-x3)*(x2-x3)+(y2-y3)*(y2-y3));double c=sqrt((x1-x3)*(x1-x3)+(y1-y3)*(y1-y3)); //三角形的三条边,用于计算角度double cs=(c*c-a*a-b*b)/(2*a*b); //cos值为其补角cos值的负数double j=acos(cs); //算出角度,弧度表示return j*r; //弧长即为弧度*半径
}
void solve(){int tt; cin >> tt;for(int ii=1;ii<=tt;ii++){cin >> n;for(int i=1;i<=n;i++)cin >> q[i].first >> q[i].second;cin >> xx >> yy;for(int i=1;i<=n;i++) ans+=cal(i);ans*=1000,ans=round(ans),ans/=1000; //四舍五入三位小数cout << "Case #" << ii << ": ";printf("%.3f\n",ans);ans=0;}
}复习了下单调栈
dp题单 线性dp 第四题 麻将 cf传送门

思路:定义 i 三连为 i,i+1,i+2 三个连续麻将,dp【i】【j】【k】表示考虑到第 i 个麻将,有 j 个 i 三连,k 个 i-1 三连
三个 i 三连等价于 三个 i,三个 i+1,三个i+2,于是存在最优解满足最多的 i 三连个数<=2
i 三连的个数选择,受到 i-1 三连和 i-2 三连的个数的影响,那么为什么不把 i-2 三连的个数也设在状态里呢,因为在转移时 dp【i-1】【k】【t】的 t 就是 i-2 三连的个数 (有点像状压,然后枚举 j,k,t 转移即可,答案为 dp【m】【0】【0】,因为没有 m+1 的麻将
代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
int a[N],m;
ll dp[N][4][4];
void solve(){cin >> n >> m;for(int i=1;i<=n;i++){int x; cin >> x;a[x]++;}for(int i=1;i<=m;i++){for(int j=0;j<=2;j++){for(int k=0;k<=2;k++){for(int t=0;t<=2;t++){if(a[i]<j+k+t) continue; //不合法dp[i][j][k]=max(dp[i-1][k][t]+j+(a[i]-j-k-t)/3,dp[i][j][k]);}}}}cout << dp[m][0][0];
}星期三:
开始做点树形dp
树形dp入门题(没有上司的舞会 洛谷传送门
思路:dp【i】【0/1】表示第 i 人来或不来
代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
ll dp[N][2];
int r[N];
vector<int>ve[N];
bool vi[N];
void dfs(int x){dp[x][1]=r[x],dp[x][0]=0;for(int v:ve[x]){dfs(v);dp[x][1]+=dp[v][0]; //x来,v肯定不来dp[x][0]+=max(dp[v][0],dp[v][1]); //x不来,v可来可不来}
}
void solve(){cin >> n;for(int i=1;i<=n;i++) cin >> r[i];for(int i=1;i<n;i++){int u,v; cin >> u >> v;ve[v].push_back(u);vi[u]=1;}int s=0;for(int i=1;i<=n;i++)if(!vi[i]){s=i; break;}dfs(s);cout << max(dp[s][0],dp[s][1]);
}dp题单 背包第三题 沙拉(很新的背包 cf传送门

思路:要求a的总和等于k倍b的总和,可以将每个物品当作价值为a【i】,重量为k*b【i】- a【i】的01背包来做,最终答案为dp【n】【0】,但因为重量可能为负数,所以考虑将下标转换一下
计算后发现重量和最大1e5,最小为-1e4,所以把dp【0】【1e4】作为起点,防止越界
代码如下:
ll n;
int k;
int a[110],b[110];
ll dp[110][110010];
void solve(){cin >> n >> k;for(int i=1;i<=n;i++) cin >> a[i];for(int i=1;i<=n;i++) cin >> b[i],b[i]=b[i]*k-a[i];memset(dp,-1,sizeof dp);dp[0][10000]=0;for(int i=1;i<=n;i++){for(int j=110000;j>=0;j--){if(j-b[i]>110000 || j-b[i]<0) continue;if(dp[i-1][j-b[i]]==-1) dp[i][j]=dp[i-1][j]; //无可转移状态else dp[i][j]=max(dp[i-1][j-b[i]]+a[i],dp[i-1][j]);}}if(!dp[n][10000]) cout << "-1";else cout << dp[n][10000];
}补周二比赛一题 F(变形弗洛伊德 cf传送门

思路:先将城市按危险度从小到大排序,三维dp数组dp【k】【u】【v】表示城市 u和 v通过危险度前 k小的城市能达到的最小距离, 转移方程如下
代码如下:
ll n;
int r[220],o[220];
ll dp[220][220][220];
bool cmp1(int a,int b){return r[a]<r[b];
}
void solve(){int tt; cin >> tt;for(int ii=1;ii<=tt;ii++){int q; cin >> n >> q;for(int i=1;i<=n;i++){cin >> r[i];o[i]=i;}sort(o+1,o+n+1,cmp1);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)cin >> dp[0][i][j];}for(int k=1;k<=n;k++){for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)dp[k][i][j]=min(dp[k-1][o[k]][j]+dp[k-1][o[k]][i],dp[k-1][i][j]);}cout << "Case #" << ii << ":\n";while(q--){int u,v,w; cin >> u >> v >> w;int k=0;for(int i=n;i;i--)if(r[o[i]]<=w){k=i; break;}cout << dp[k][u][v] << "\n";}}
}星期四:
dp题单里做了道2200的图论 cf传送门

思路:对于一个满足题目条件的n个点的连通块来说,如果无环,至少需要 n-1条边构成一棵树,如果有环,则至少需要n条边构成一个环
不考虑m的情况下,答案最大是n,即把n个点连成一个环,而对于无环的连通块,则可使答案减一
根据 m个要求建立有向图,对每个连通块判断有无环,没被m提到的点也会被拓扑排序,视为一个点的树,最后答案为 n减去树联通量的个数
代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
int m;
vector<int>ve[N];
int in[N],fa[N];
bool vi[N],d[N];
int fnd(int x){return fa[x]==x?x:fa[x]=fnd(fa[x]);
}
void tp(){queue<int>qu;for(int i=1;i<=n;i++)if(!in[i]) qu.push(i),vi[i]=1;while(!qu.empty()){int t=qu.front(); qu.pop();for(int v:ve[t]){in[v]--;if(!in[v]) qu.push(v),vi[v]=1; //拓扑排序判断有无环}}
}
void solve(){cin >> n >> m;for(int i=1;i<=n;i++) fa[i]=i;while(m--){int u,v; cin >> u >> v;ve[u].push_back(v);in[v]++;u=fnd(u),v=fnd(v);if(u!=v) fa[v]=u; //并查集维护连通块}tp();map<int,int>mp;for(int i=1;i<=n;i++)if(!vi[i]) d[fnd(i)]=1; //没在tp里出现过,说明此联通量有环for(int i=1;i<=n;i++)if(!d[fnd(i)]) mp[fnd(i)]++; //如果无环,此联通量为树cout << n-mp.size();
}dp题单 状压第四题(3rd missed) cf传送门
加深了我对状压的认知,但还有许多疑惑
思路:dp【mask】【i】表示经过点集为mask,目标点为 i的路径数
参考题解:Codeforces C. A Simple Task(状态压缩dp) - 小张人 - 博客园 (cnblogs.com)
代码如下:
ll n;
int m;
bool ve[22][22];
ll dp[1<<20][22];
ll ans;
void solve(){cin >> n >> m;for(int i=1;i<=m;i++){int u,v; cin >> u >> v;ve[u][v]=ve[v][u]=1;}for(int i=1;i<=n;i++) dp[1<<(i-1)][i]=1;for(int mask=0;mask<1<<n;mask++){for(int u=1;u<=n;u++){if(!dp[mask][u]) continue;int st=__builtin_ctz(mask)+1; //路径的起点for(int v=st;v<=n;v++){ //下一个点需大于等于起点,状态才合法if(!ve[u][v]) continue;int nmask=mask|1<<v-1;if(!(mask&1<<v-1)) dp[nmask][v]+=dp[mask][u];else if(v==st) ans+=dp[mask][u]; //目标点就是起点,即成环}}}ans-=m,ans/=2;cout << ans;
}星期五:
dp题单 线性dp 第五题(偏区间dp cf传送门

思路:虽在线性dp题单,但数据范围和题目给出的操作让人很容易想到区间dp,也确实是区间dp
f【l】【r】表示 l 到 r 范围内最大可合成的数,使用区间dp预处理,然后找出最小的分块方式
代码如下:
ll n;
int a[550];
int f[550][550];
int dp[550];
void solve(){cin >> n;memset(f,-1,sizeof f);for(int i=1;i<=n;i++){cin >> a[i];f[i][i]=a[i];}for(int len=2;len<=n;len++){for(int l=1;l+len-1<=n;l++){int r=l+len-1;for(int k=l;k<r;k++){if(f[l][k]==-1 || f[k+1][r]==-1) continue;if(f[l][k]!=f[k+1][r]) continue;f[l][r]=f[l][k]+1; //合成}}}memset(dp,0x3f,sizeof dp);dp[0]=0;for(int i=1;i<=n;i++){for(int l=1;l<=i;l++){if(f[l][i]==-1) continue;dp[i]=min(dp[l-1]+1,dp[i]); //找出最佳分块方案}}cout << dp[n];
}线性dp 第六题(仍是区间dp cf传送门

题意:给一字符串,q次询问,每次给出 l 和 r,求 s下标 l到 r的子串中有多少子串为回文串
思路:isp【l】【r】表示 l 到 r 子串是否为回文串,用区间dp预处理
dp【l】【r】表示 l 到 r 子串中有多少子串为回文串,用容斥原理求出(?
代码如下:
ll n;
string s;
bool isp[5050][5050];
int dp[5050][5050];
void solve(){cin >> s;n=s.size(),s=" "+s;for(int i=1;i<=n;i++){isp[i][i]=1;if(i<n && s[i]==s[i+1]) isp[i][i+1]=1;dp[i][i]=1;dp[i][i+1]=2;dp[i][i+1]+=(isp[i][i+1]==1);}for(int len=3;len<=n;len++){for(int l=1;l+len-1<=n;l++){int r=l+len-1;if(s[l]==s[r] && isp[l+1][r-1]) isp[l][r]=1;}}for(int len=3;len<=n;len++){for(int l=1;l+len-1<=n;l++){int r=l+len-1;dp[l][r]=dp[l][r-1]+dp[l+1][r]-dp[l+1][r-1]+isp[l][r];//容斥原理}}int q; cin >> q;while(q--){int l,r; cin >> l >> r;cout << dp[l][r] << "\n";}
}星期六:
下午图森未来杯
晚上ABC351止步于D
cf round941 div2止步于D
周日:
ABC351的D比较简单(怎么赛时没出 传送门
思路:暴力bfs每个点,复杂度为O(n^4),毫无疑问会T,其实只需对每个连通块处理一次即可
代码如下:
ll n;
int h,w;
char c[1010][1010];
bool ifm[1010][1010];
bool vi[1010][1010];
int dx[]={0,0,-1,1};
int dy[]={-1,1,0,0};
map<PII,int>mp;
int dfs(int x,int y){if(ifm[x][y]){if(mp[{x,y}]) return 0;mp[{x,y}]=1; return 1; //对磁铁邻点的特殊处理}vi[x][y]=1;int res=1;for(int i=0;i<4;i++){int xx=x+dx[i],yy=y+dy[i];if(xx<1 || xx>h || yy<1 || yy>w || vi[xx][yy]) continue;if(c[xx][yy]=='#') continue;res+=dfs(xx,yy);}return res;
}
void solve(){cin >> h >> w;for(int i=1;i<=h;i++){for(int j=1;j<=w;j++){cin >> c[i][j];if(c[i][j]=='#')for(int k=0;k<4;k++) ifm[i+dx[k]][j+dy[k]]=1;}}int ans=0;for(int i=1;i<=h;i++){for(int j=1;j<=w;j++){if(c[i][j]=='#' || vi[i][j]) continue;if(ifm[i][j]){ans=max(ans,1); continue;}ans=max(ans,dfs(i,j));mp.clear();}}cout << ans;
}cf round941 的 D,很刁的一道构造 cf传送门

思路:首先如果没有 k 的限制,会很自然想到二进制的构造方案,那么问题就变成了如何魔改二进制,使其唯独不能组成 k
不能组成 k,比较自然的想到先删去 k 的二进制表达最高位,记为 h位,没了 2^h后,再看看除 k之外的数如何组成,结论是需要额外添加三个数,k-2^h,k+1,k+1+2^h
第一种数是 v < 2^h,删去 2^h并不会影响此类数
第二种是 2^h <= v < k,这时所有小于 k的数和为 2^h-1,补上 k-2^h,和为 k-1,能覆盖 <k的数,因为总和与v的差值即多出来的数值为 k-1-v < 2^h,由第一类数可知多余数值能够被删去
第三种是 v >= k,考虑先构造出 v-k-1,若 2^h 不在此构造内,补上 k+1,否则补上 k+1+2^h
代码如下:
ll n;
void solve(){ll k; cin >> n >> k;int idx=__lg(k); //k的二进制最高位cout << 22 << "\n";for(int i=0;i<20;i++){if(i==idx) continue;cout << (1<<i) << " ";}cout << k-(1<<idx) << " " << k+1 << " " << 1ll*k+1+(1ll<<idx) << "\n";
}dp题单 数位dp最后一道 后缀%k cf传送门

思路:从个位向第 n位 d,dfs有三个参数, 分别表示当前 d到的位数, 当前数对 k的模数, 当前数是否>0
若当前数 >0且模 k为0,则为合法后缀, 剩余位任意填值, 只需注意第 n位不能为0, 结果可直接用快速幂计算. 模数的继承因为是从低位往高位 d, 所以新添位对于 k的模数也需要用快速幂计算.
代码如下:
ll n;
int k,m;
ll dp[1010][110][2];
ll qpow1(int n){ //计算答案if(n==0) return 1;if(n==1) return 10;ll s=qpow1(n/2);s=s*s%m;if(n&1) s=s*10%m;return s;
}
ll qpow2(int n){ //计算模数if(n==0) return 1;if(n==1) return 10;ll s=qpow2(n/2);s=s*s%k;if(n&1) s=s*10%k;return s;
}
ll dfs(int now,int mo,bool if1){if(now>n) return mo==0;if(dp[now][mo][if1]!=-1) return dp[now][mo][if1];ll res=0;if(!mo && now>1 && if1) res=qpow1(n-now)*9;else{for(int i=now==n;i<=9;i++)res+=dfs(now+1,(mo+i*qpow2(now-1)%k)%k,if1|(i>0)),res%=m;}return dp[now][mo][if1]=res;
}
void solve(){cin >> n >> k >> m;memset(dp,-1,sizeof dp);cout << dfs(1,0,0);
}这篇关于24.4.28(板刷dp,拓扑判环,区间dp+容斥算回文串总数)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




